 Зъбни колела
Зъбни колела
Това са записки върху зъбните предавки, които отдавна са детайлно описани,
но за мен се те оказаха нещо ново.
Автор на еволвентната постановка е Ойлер 1760.
В действителност тук е разгледан само характерния случай на стандартна цилиндрична зъбна двойка с еволвентен профил.
Написах една програма за изследване на такива двойки 670kb GEAR.EXE Модел на двойка зъбни колела.
 Конци и макари
Конци и макари
Има един клас криви, наречени еволвентни, на които трябва да обърнем внимание - заради изложението по-нататък.
На чист български език фразата "еволвентна крива" би трябвало да се преведе като "развиваща крива" - Геометрично място на точки,
съвпадащи с края на развиваща се нишка от някаква форма или повърхност.
В много текстове се срещат уточняващи термини, като еволюти и инволюти - зависи от това дали
развиваме, или навиваме нишката.
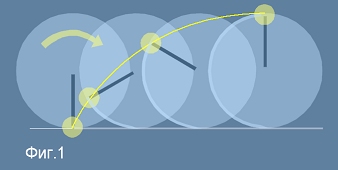
Най простия случай, при който една окръжност се търкаля върху права е илюстриран на Фиг.1.
Жълтата крива има подобен характер - ако окръжността е макара и върху нея се навива нишка,
края на нишката ще описва такава крива. Сега ще си поставим задача да намерим аналитичен израз за
тази крива.
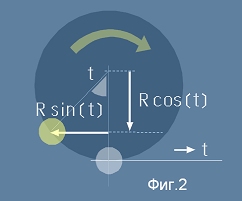 Най-удобно тя се представя по параметричен начин.
Да поставим началото на координатната система в допирната точка между окръжността (с радиус =1) и
правата - бялото кръгче на Фиг.2.
Разглеждаме периферната точка означена на Фиг.2 като жълто кръгче. Тази точка участвува в две независими движения.
Едното от тях е равномерно праволинейно движение надясно, със скорост t, защото търкалянето е без хлъзгане.
Другото е равномерно движение по окръжност.
Движението на центъра на окръжността се описва от две уравнения:
Най-удобно тя се представя по параметричен начин.
Да поставим началото на координатната система в допирната точка между окръжността (с радиус =1) и
правата - бялото кръгче на Фиг.2.
Разглеждаме периферната точка означена на Фиг.2 като жълто кръгче. Тази точка участвува в две независими движения.
Едното от тях е равномерно праволинейно движение надясно, със скорост t, защото търкалянето е без хлъзгане.
Другото е равномерно движение по окръжност.
Движението на центъра на окръжността се описва от две уравнения:
x = t ; y = 1
Но към това движение, за всяка периферна точка се прибавя движението по окръжност.
То се описва от друга двойка уравнения:
x = -sin(t) ; y = -cos(t)
Като сбор на горните две двойки, XY-координатите представляват следните функции от времето:
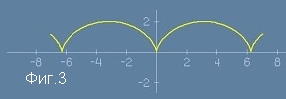 x = t - sin(t)
x = t - sin(t)
y = 1 - cos(t).
Тези две уравнения определят параметрична крива, чиято графика е показана на Фиг.3.
Същата графика може да се построи онлайн от страницата Параметрични криви.
След казаното дотук, кривата се определя като инволюта, защото нишката се навива.
Но описаното действие е симетрично спрямо t и ако нишката се развива,
ще получим същата крива. В такъв случай тя ще се нарича
Еволюта
 Да си представим, че нишка се развива от неподвижен цилиндър с радиус 1 - виж Фиг.4.
Да си представим, че нишка се развива от неподвижен цилиндър с радиус 1 - виж Фиг.4.
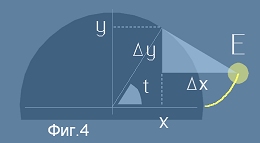 На тази фигура краят на нишката е означен с буква E. Да разгледаме светлия правоъгълен триъгълник.
Горният му остър ъгъл е равен на ъгъла на развиване t, защото това са ъгли с взаимно перпендикулярни рамене.
Дължината на развилата се вече нишка - хипотенузата - е равна на t (радиусът е 1).
За двата катета - делта x и делта y, можем да напишем
На тази фигура краят на нишката е означен с буква E. Да разгледаме светлия правоъгълен триъгълник.
Горният му остър ъгъл е равен на ъгъла на развиване t, защото това са ъгли с взаимно перпендикулярни рамене.
Дължината на развилата се вече нишка - хипотенузата - е равна на t (радиусът е 1).
За двата катета - делта x и делта y, можем да напишем
 . [1]
. [1]
Координатите на точката, в която се отлепя нишката
- горния връх на същия триъгълник, са
 . [2]
. [2]
От Фиг.4 , както и от [1] и [2] се вижда какви ще бъдат координатите на точката E:
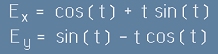 . [3]
. [3]
Последните две равенства определят параметрична крива, наречена еволюта.
Графиката на кривата може да се види на Фиг.5 или да бъде построена в момента от
този линк
.
Най-често, в профила на един зъб от зъбно колело, триещият се участък е с такава форма.
 Хлъзгане и Търкаляне
Хлъзгане и Търкаляне
Случвало се е хора са ми казват, че повърхностите на зъбните колела се търкалят една върху друга без хлъзгане, тоест
практически без триене.
Внимателният поглед върху процеса показва, че това не е възможно.
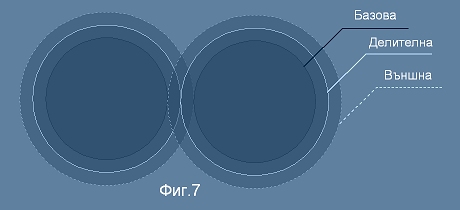
 За да няма хлъзгане, а само търкаляне, условието е относителното движение на двете повърхности да има
само нормална компонента, а допирателната да е нулева (виж Фиг.6).
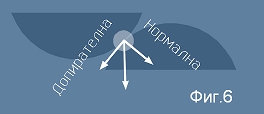
За всяко зъбно колело има три важни окръжности - Базова, Делителна и Външна.
Тези окръжности са показани на Фиг.7. Двойките зъбни колела се правят така,
че делителните им окръжностти да са допирателни. Зъбните лица могат да контактуват в цялата
област между Базовата и Външната окръжност. Тази област има крайни размери и в нея
има една единствена двойка окръжности,
за които относителното движението няма допирателна а има само нормална компонента
- това са двете делителни окръжности. Следователно допир без хлъзгане има в една - единствена точка -
точката, в която се допират Делителните. В останалите случаи относителната скорост варира около нулата,
така че хлъзгането е минимално.
За да няма хлъзгане, а само търкаляне, условието е относителното движение на двете повърхности да има
само нормална компонента, а допирателната да е нулева (виж Фиг.6).
За всяко зъбно колело има три важни окръжности - Базова, Делителна и Външна.
Тези окръжности са показани на Фиг.7. Двойките зъбни колела се правят така,
че делителните им окръжностти да са допирателни. Зъбните лица могат да контактуват в цялата
област между Базовата и Външната окръжност. Тази област има крайни размери и в нея
има една единствена двойка окръжности,
за които относителното движението няма допирателна а има само нормална компонента
- това са двете делителни окръжности. Следователно допир без хлъзгане има в една - единствена точка -
точката, в която се допират Делителните. В останалите случаи относителната скорост варира около нулата,
така че хлъзгането е минимално.
Изпълнение
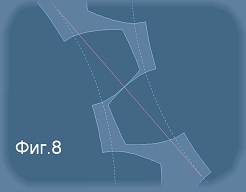
Базовата (основната) окръжност за едно зъбно колело (виж Фиг.7) е тази, от която става развиването на еволютата
в по-горното обяснение. На Фиг.8 са нарисувани силуети на два допиращи се зъба заедно с базовите им окръжности.
Тъй като и двете повърхности са развивки, във всяка своя точка те са перпендикулярни на коя да е допирателна към
основната си (базова) окръжност. В частност те са перпендикулярни към онази допирателна, която е обща за
двете базови окръжности - червената линия на Фиг.8. Тази линия се нарича линия на зацепване (на англ. Presure Line),
може би превода е линия на натиск или линия на напрежение.
Допирната точка със сигурност е обща за три линии - двете повърхности и линията на натиска.
Това място може да варира в зависимост от ъгъла на завъртане, както и от разстоянието между
центровете на двете окръжности, но свойството на повърхностите да бъдат винаги успоредни една на друга
и перпендикулярни към силовата права ще се запази.
 Правила
Правила
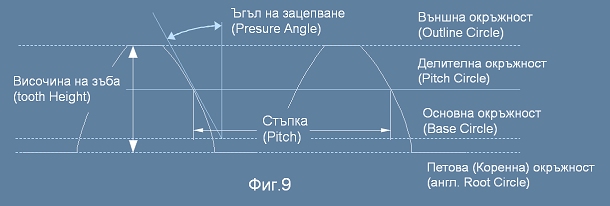
На Фиг.9 са изобразени главните технически термини, с които инженерите обясняват зъбните колела.
На тази тема има правила, свързани с геометрията, стандарт и технология.
Благодарение на стандартизацията, в общия случай са достатъчни две числа, за да бъде определен профила на едно зъбно колело.
Едното е стъпката, а другото - броя на зъбите.
Ето няколко от правилата за проектиране при зъбни колела с 10 и повече зъба:
1. Еволвентния профил започва от основната окръжност.
2. Делителната окръжност е по средата между основната и външната.
3. Височината на зъба е малко над (2/пи) от стъпката.
4. Разстоянието от делителната до външната е половината височина.
 5. Между два зъба разстоянието е маалко повече от половин стъпка, мерена по делителната.
5. Между два зъба разстоянието е маалко повече от половин стъпка, мерена по делителната.
6. Ъгъла на зацепване по БДС (също и по други стандарти) е 20 ъглови градуса.
Проектиране
Току-що изброените правила са само начални. Ако искаме да проектираме действително зъбно колело, трябват още.
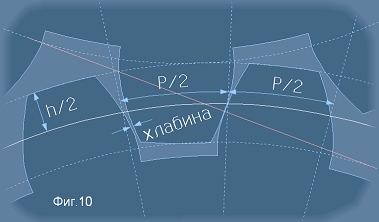
На Фиг.10 са изобразени няколко оиентировъчни съотношения, които трябва да се вземат предвид.
С буква P е означена стъпката, с буква h е означена височината на зъба.
Бялата линия е Делителната (Стъпковата) окръжност. Предполага се движение надясно и горно движещо колело.
С моята програма, цитирана най-горе успях да моделирам
ъгълът на зацепване е между 9 и 27 ъглови градуса и брой на зъбите е 4 или повече.
Промишлените образци се придържат към ъгли 14,20,22 градуса и брой на зъбите - 10 и повече.
Процесът на зацепване се илюстрира от
тази 10-секундна анимация
, извлечена от същата програма.
В анимацията са изобразени базовите и делителните окръжности.
С червен цвят е означена линията на зацепване. Направена е така, че да проследи малко повече от една стъпка.
 Изпълнение
Изпълнение
Понякога стъпката, разделена на пи се нарича модул.
Има известна формула за външния диаметър на зъбните колела. Ако N е броя на зъбите, а MOD е модула,
външният диаметър (англ. OD-Out Diameter) спазва условието:
OD = (N+2) x MOD
С програмата "gear.exe" направих колелото, показано на фиг.11. Модул 1 (всъщност стъпка едно пи), 30 зъба, 18 градуса ъгъл на натиск.
6 спици, осев отвор 1.9 мм. Дебелината е 4.3 мм - такъв материал имах.
Шублерът показа външен диаметър 31.8 при теоретичен размер 32 мм. Това е нормално,
при малки размери, за външния диаметър, хлабините и подзъбните кухини трябва
да се оставя относително по-голям толеранс, иначе има риск от лошо зацепване.
Процедурата е: От програмата "gear.exe" се излъчва plt-файл, който внасям в
рисувачката (Radis Vector Editor-RVE.EXE), публикувана на страницата "безплатни програми",
после оттам задавам размери и други подробности, след което от рисувачката изнасям g-code
към CNC-машината.
Р.Ж. Създаден 26.12.2011 Последна редакция 16.12.2013
Начална страница
 Зъбни колела
Зъбни колела Конци и макари
Конци и макари Най-удобно тя се представя по параметричен начин.
Да поставим началото на координатната система в допирната точка между окръжността (с радиус =1) и
правата - бялото кръгче на Фиг.2.
Разглеждаме периферната точка означена на Фиг.2 като жълто кръгче. Тази точка участвува в две независими движения.
Едното от тях е равномерно праволинейно движение надясно, със скорост t, защото търкалянето е без хлъзгане.
Другото е равномерно движение по окръжност.
Движението на центъра на окръжността се описва от две уравнения:
Най-удобно тя се представя по параметричен начин.
Да поставим началото на координатната система в допирната точка между окръжността (с радиус =1) и
правата - бялото кръгче на Фиг.2.
Разглеждаме периферната точка означена на Фиг.2 като жълто кръгче. Тази точка участвува в две независими движения.
Едното от тях е равномерно праволинейно движение надясно, със скорост t, защото търкалянето е без хлъзгане.
Другото е равномерно движение по окръжност.
Движението на центъра на окръжността се описва от две уравнения: x = t - sin(t)
x = t - sin(t) Да си представим, че нишка се развива от неподвижен цилиндър с радиус 1 - виж Фиг.4.
Да си представим, че нишка се развива от неподвижен цилиндър с радиус 1 - виж Фиг.4. На тази фигура краят на нишката е означен с буква E. Да разгледаме светлия правоъгълен триъгълник.
Горният му остър ъгъл е равен на ъгъла на развиване t, защото това са ъгли с взаимно перпендикулярни рамене.
Дължината на развилата се вече нишка - хипотенузата - е равна на t (радиусът е 1).
За двата катета - делта x и делта y, можем да напишем
На тази фигура краят на нишката е означен с буква E. Да разгледаме светлия правоъгълен триъгълник.
Горният му остър ъгъл е равен на ъгъла на развиване t, защото това са ъгли с взаимно перпендикулярни рамене.
Дължината на развилата се вече нишка - хипотенузата - е равна на t (радиусът е 1).
За двата катета - делта x и делта y, можем да напишем . [1]
. [1] . [2]
. [2]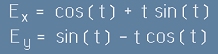 . [3]
. [3] Хлъзгане и Търкаляне
Хлъзгане и Търкаляне За да няма хлъзгане, а само търкаляне, условието е относителното движение на двете повърхности да има
само нормална компонента, а допирателната да е нулева (виж Фиг.6).
За всяко зъбно колело има три важни окръжности - Базова, Делителна и Външна.
Тези окръжности са показани на Фиг.7. Двойките зъбни колела се правят така,
че делителните им окръжностти да са допирателни. Зъбните лица могат да контактуват в цялата
област между Базовата и Външната окръжност. Тази област има крайни размери и в нея
има една единствена двойка окръжности,
за които относителното движението няма допирателна а има само нормална компонента
- това са двете делителни окръжности. Следователно допир без хлъзгане има в една - единствена точка -
точката, в която се допират Делителните. В останалите случаи относителната скорост варира около нулата,
така че хлъзгането е минимално.
За да няма хлъзгане, а само търкаляне, условието е относителното движение на двете повърхности да има
само нормална компонента, а допирателната да е нулева (виж Фиг.6).
За всяко зъбно колело има три важни окръжности - Базова, Делителна и Външна.
Тези окръжности са показани на Фиг.7. Двойките зъбни колела се правят така,
че делителните им окръжностти да са допирателни. Зъбните лица могат да контактуват в цялата
област между Базовата и Външната окръжност. Тази област има крайни размери и в нея
има една единствена двойка окръжности,
за които относителното движението няма допирателна а има само нормална компонента
- това са двете делителни окръжности. Следователно допир без хлъзгане има в една - единствена точка -
точката, в която се допират Делителните. В останалите случаи относителната скорост варира около нулата,
така че хлъзгането е минимално.
 Правила
Правила 5. Между два зъба разстоянието е маалко повече от половин стъпка, мерена по делителната.
5. Между два зъба разстоянието е маалко повече от половин стъпка, мерена по делителната. Изпълнение
Изпълнение