 Движение по окръжност
Движение по окръжност
Тук са дадени определения и коментари за ъгловите версии на понятията скорост, ускорение, импулс, сила, инерция в класическата
механика.
Четенето изисква да знаем значението на изразите производна
и векторно произведение.
Тези неща са достъпни от учебника на Станчо Павлов.
Въведение
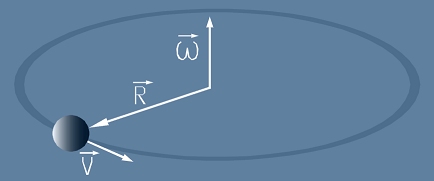 Да предположим, че едно тяло (материална точка) се движи с една и съща по големина скорост по окръжност.
Това означава, че има твърда връзка, която запазва разстоянието между разглежданата точка и центъра на окръжността.
По-долу ще предполагаме, че това разстояние е ненулево.
Добре е да уговорим и понятието ос на въртене - права, минаваща през центъра
и перпендикулярна на скоростта, с която се движи тялото.
Всички следващи определения са спрямо този център и ос.
Добре е също да уточним какво е дясна координатна система - това е такава
система координатни оси, че ако застанем в центъра и гледаме към първи квадрант/октант,
подредбата на осите ще се върти надясно (по часовниковата стрелка).
Тук ще подразбираме дясна координатна система.
Да предположим, че едно тяло (материална точка) се движи с една и съща по големина скорост по окръжност.
Това означава, че има твърда връзка, която запазва разстоянието между разглежданата точка и центъра на окръжността.
По-долу ще предполагаме, че това разстояние е ненулево.
Добре е да уговорим и понятието ос на въртене - права, минаваща през центъра
и перпендикулярна на скоростта, с която се движи тялото.
Всички следващи определения са спрямо този център и ос.
Добре е също да уточним какво е дясна координатна система - това е такава
система координатни оси, че ако застанем в центъра и гледаме към първи квадрант/октант,
подредбата на осите ще се върти надясно (по часовниковата стрелка).
Тук ще подразбираме дясна координатна система.
Окръжността и центъра ни подтикват да мислим за полярни координати, в които позицията се определя от ъгъл и радиус.
И действително големината на ъгловата скорост може да се определи като първа производна по времето на променящият се централен ъгъл.
Но както линейната, така и ъловата скорост е вектор, затова ще трябва да кажем още, че посоката на вектора е по оста на въртене.
До същото ще стигнем и чрез написаното на първо място по-долу с вектори. В този текст векторите са означени като:
 (омега) - ъглова скорост;
(омега) - ъглова скорост;
 - линейна скорост;
- линейна скорост;
 - линейно ускорение;
- линейно ускорение;
 - ъглово ускорение;
- ъглово ускорение;
 - въртящ момент (момент на сила спрямо ос);
- въртящ момент (момент на сила спрямо ос);
 - момент на импулса;
- момент на импулса;
Ъглова скорост - определение:
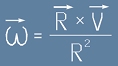 .
.
Ъгловата скорост се определя като пропорционална на векторното произведение между радиус-вектора на тялото R и вектора на линейната
скорост V. При векторното произведение, резултатът по посока е перпендикулярен на двата аргумента и числовата му стойност е колкото
лицето на успоредника, образуван от тях. Мярката за ъглова скорост е [радиан / секунда].
[отклонение 1]
Векторните произведения са антикомутативни, тоест (AxB = -BxA), разпределяеми, тоест (Ax(B + C) = AxB + AxC),
прозрачни за числов множител, тоест ако k e число, то k(AxB)=(kA)xB=Ax(kb)
и имат специален начин за последователно прилагане, наречен двойно векторно произведение:
Ax(BxC) = B(A.C) - C(A.B) /точката е знак за скаларно произведение/.
Да погледнем числителя в дясната страна на горното определение и да го умножим отдясно векторно с R. Ще получим
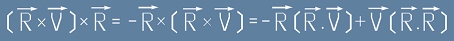 . Първото събираемо е нула, защото съдържа като множител скаларното произведение на два взаимно перпендикулярни
вектора R.V;
. Първото събираемо е нула, защото съдържа като множител скаларното произведение на два взаимно перпендикулярни
вектора R.V;
[/край на отклонение 1]
Да умножим двете страни на определението отдясно с R и ще намерим линейната скорост:  [1].
[1].
[отклонение 2]
Линейно ускорение
Ускорението е промяна в скоростта за единица време.
Щом тялото не се движи по права, векторът на скоростта се променя и това означава,
че движението по окръжност винаги е съпроводено с ускорение. Силата, която предизвиква това ускорение е
от уговорената по-горе твърда връзка, запазваща разстоянието до центъра - нарича се центростремителна сила.
Наличието на ускорение е съществена разлика в сравнение с равномерното праволинейно движение. Например
не ни позволява да третираме координатна система - привързана към тялото - като инерциална.
Следват малко геометрични разсъждения за големината на
това ускорение:
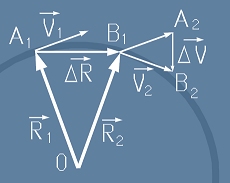 Да разгледаме две точки A1 и B1 от движението, с радиус-вектори R1 и R2; Да означим скоростите с V1 и V2.
Да построим мислен вектор от B1 до A2, равен по посока и големина с V1.
Да разгледаме две точки A1 и B1 от движението, с радиус-вектори R1 и R2; Да означим скоростите с V1 и V2.
Да построим мислен вектор от B1 до A2, равен по посока и големина с V1.
Да забележим подобието на триъгълниците O A1 B1 ~ B1 A2 B2.
Ако векторите R и V са с постоянна дължина ( |R1| = |R2| и |V1| = |V2| ), то 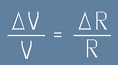 ,
,
откъдето следва, че промяната в скоростта е 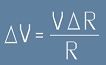 . Да разделим двете страни
на това равенство с интервала време между двете положения на точката:
. Да разделим двете страни
на това равенство с интервала време между двете положения на точката:
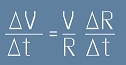 . При малки временни интервали клонящи към нула, лявата страна на това равенство
по дефиниция клони към ускорението, а последния множител клони към скоростта V. Така получихме оценка за големината
на ускорението:
. При малки временни интервали клонящи към нула, лявата страна на това равенство
по дефиниция клони към ускорението, а последния множител клони към скоростта V. Така получихме оценка за големината
на ускорението: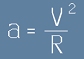 . Лесно е да съобразим, че като вектор
. Лесно е да съобразим, че като вектор 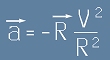 .
.
Изразено чрез ъгловата скорост от [1], линейното ускорение е: 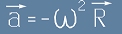 [2].
[2].
Посоката на линейното ускорение е към центъра, затова то често се нарича центростремително ускорение.
[/край на отклонение 2]
Ъглово ускорение - определение
Ъгловото ускорение се определя като производна на ъгловата скорост по времето: 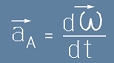 .
.
Както виждаме, ъгловото ускорение е по смисъл различно от линейното. Размерността му е [радиан/секунда2]
Определението е избрано
първо: за да е ясно, че посоката на вектора е по оста на въртене;
второ: по този начин то добре се съгласува с уравнението на Нютон F=ma (виж по-долу).
Кинетична енергия: 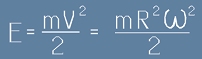 .
Енергията е скалар. Тук тя е само представена чрез ъгловата скорост, тоест това не е определение за енергия,
но е написано, защото подпомага следващото.
.
Енергията е скалар. Тук тя е само представена чрез ъгловата скорост, тоест това не е определение за енергия,
но е написано, защото подпомага следващото.
Инерчен момент - определение:  се определя като Инерчен момент. Това е мярка за
инертността на въртящото се тяло, тя играе роля, подобна на масата (m) при постъпателно движение. От определението се
вижда, че мярката за инерчен момент е [килограм х метър х метър].
се определя като Инерчен момент. Това е мярка за
инертността на въртящото се тяло, тя играе роля, подобна на масата (m) при постъпателно движение. От определението се
вижда, че мярката за инерчен момент е [килограм х метър х метър].
В такъв случай енергията може да бъде изразена като 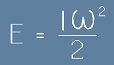 ,
което е подобие на равенството E=mv2/2.
,
което е подобие на равенството E=mv2/2.
Въртящ момент - определение: 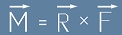
Ако една сила F действува на тялото, векторното произведение
между радиус-вектора към тялото и вектора на тази сила се определя като въртящ момент (момент на сила) спрямо центъра. Мярката за въртящ момент е [нютон х метър].
Втори принцип на Нютон
Да допуснем, че сила F действува на тялото. В някакъв интервал от време скоростта ще нарастне от V1 до V2.
Съгласно [1] тази промяна се изразява като  [3],
[3],
където индексите 1 и 2 съответствуват на начало и край на разглеждания интервал.
Ако означим с делта промените, умаляемото в дясната страна ще придобие вида 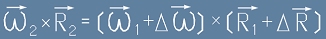 ,
а след разкриване на скобите равенството [3] ще изглежда така:
,
а след разкриване на скобите равенството [3] ще изглежда така:
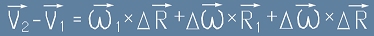 .
.
Да разделим промяната в скоростта на интервала време: 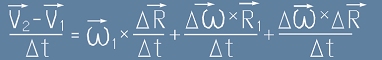 [4]
[4]
и да си представим интервал време клонящ към нула. Лявата страна на [4] клони към общото ускорение.
В дясната страна на [4] третото събираемо клони към нула. В първото събираемо можем да съобразим, че
 , където векторът V е линейната скорост;
, където векторът V е линейната скорост;
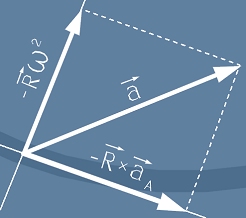
Линейната скорост V може да бъде изразена чрез ъгловата, по формула [1],
след което първото събираемо в дясната страна на [4] ще бъде
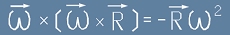 .
.
Tази съставка на ускорението очевидно съвпада с [2] - центростремителното ускорение.
Тя е насочена срещу радиуса и не променя ъгловата скорост.
Втората съставка от дясната страна на [4] може да се изрази като
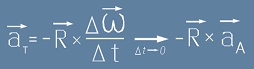 .
Двете съставки на ускорението от [4] съответствуват на две съставки в силата - радиална и допирателна.
Радиалната съставка е центростремителната сила.
.
Двете съставки на ускорението от [4] съответствуват на две съставки в силата - радиална и допирателна.
Радиалната съставка е центростремителната сила.
Да разгледаме допирателната съставка (тази която е перпендикулярна на радиус-вектора).
За нея в уравнението на Нютон ще получим 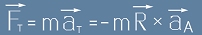 .
Ако умножим с отляво векторно с R двете страни, ще получим
.
Ако умножим с отляво векторно с R двете страни, ще получим 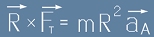 .
.
В ляво на последното равенство е въртящия момент, а изразът mR2 е инерчния момент. Така стигаме до равенството
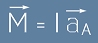 [6],
[6],
което е аналог на Втория принцип на Нютон.
Интересно е, че ако силата е изцяло радиална - допирателната съставка е нула - ускорението е изцяло центростремително,
което води до движение по окръжност (при постоянна по големина сила).
Такъв случай се наблюдава при движение на електрон в еднородно магнитно поле, тъй като
магнитните силови линии са перпендикулярни на тока.
Момент на импулса - определение: Векторът 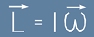 се определя като момент на импулса.
Това е аналог на импулса (p=mv) при постъпателно движение и се запазва във времето, освен ако въртящ момент не го промени.
Ако въртящият момент е нула, в дясно на [6] ще е нула ъгловото ускорение,
което означава постоянна ъглова скорост и постоянен момент на импулса.
се определя като момент на импулса.
Това е аналог на импулса (p=mv) при постъпателно движение и се запазва във времето, освен ако въртящ момент не го промени.
Ако въртящият момент е нула, в дясно на [6] ще е нула ъгловото ускорение,
което означава постоянна ъглова скорост и постоянен момент на импулса.
_______________________________________
Без да излагаме засега теория на въртящо се твърдо тяло, нека разгледаме тези примери:
Пример 1
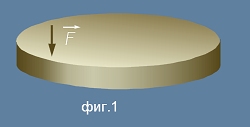
 Да си представим неподвижен метален диск, висящ в безтегловност и сила F,
която действува в периферията му перпендикулярно на плоскостта, за кратко време - нека смятаме това за удар - както е показано на фиг.1.
Да си представим неподвижен метален диск, висящ в безтегловност и сила F,
която действува в периферията му перпендикулярно на плоскостта, за кратко време - нека смятаме това за удар - както е показано на фиг.1.
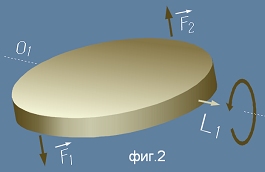
Подобно действие биха имали двойка сили F1 и F2, действуващи в противоположни посоки и с еднаква големина.
Резултатът ще бъде, че дискът ще се завърти около оста О1 и
заедно с това ще придобие момент на импулса L1. (виж фиг.2)
Такова поведение има монетата, която хвърляме при "ези-тура".
Пример 2
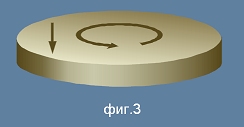
 Нека сега си представим същия диск в безтегловност, но този път въртящ се около своята ос и следователно
имащ някакъв начален момент на импулса - вектор WP0. Да нанесем същия удар по периферията, както в по-горе,
в пример 1. - виж фиг.3
Нека сега си представим същия диск в безтегловност, но този път въртящ се около своята ос и следователно
имащ някакъв начален момент на импулса - вектор WP0. Да нанесем същия удар по периферията, както в по-горе,
в пример 1. - виж фиг.3
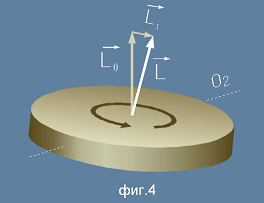
Този път дискът никак няма да подаде в посоката, в която е нанесен удара. По "неочакван" начин той ще промени
своята ос на въртене, но така, че ще се завърти около нова ос - O2 - близка до правата, съединяваща
точката на удара и центъра на въртене. (виж фиг.4)
Под действие на въртящия момент на силата F възниква промяна в момента на импулса, означен на фиг.4
като вектор L1. Ако дискът беше неподвижен, както в пример 1, това щеше да е и целият момент на импулса,
който се появява като следствие от удара F (така е изобразен и на фиг.2). Но в този слуай придобития момент L1
се прибавя към началния вектор L0. Сумарно новият момент на импулса е L - бялата стрелка
на фиг.4 и посоката му е получена по правилото за събиране на векторите L0 и L1.
Пример 3
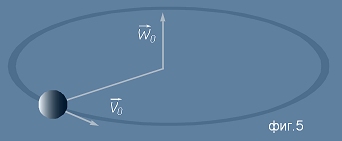
 Горния пример (2) може да се представи по-разбираемо, ако заменим диска с едно малко по размери тяло което се върти около
център - например е свързано с твърда нишка. Да означим с V0 линейната скорост в началото и с W0 - ъгловата скорост (фиг.5).
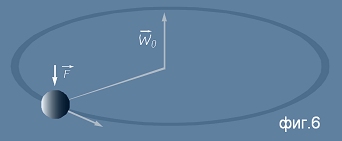
Да повторим удара от пример 1 със сила F действуваща върху тялото и перпендикулярна на плоскостта на въртене - виж фиг.6.
Горния пример (2) може да се представи по-разбираемо, ако заменим диска с едно малко по размери тяло което се върти около
център - например е свързано с твърда нишка. Да означим с V0 линейната скорост в началото и с W0 - ъгловата скорост (фиг.5).
Да повторим удара от пример 1 със сила F действуваща върху тялото и перпендикулярна на плоскостта на въртене - виж фиг.6.
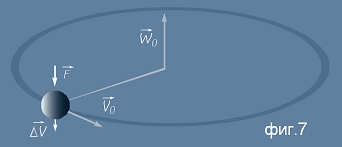
 Силата F ще придаде на тялото ускорение и заедно с това промяна
Силата F ще придаде на тялото ускорение и заедно с това промяна
в линейната скорост  -
виж фиг.7. Тази промяна ще се насложи към текущия вектор на скоростта и тялото ще придобие нова скорост
V1 - векторна сума на началната и придобитата скорост:
-
виж фиг.7. Тази промяна ще се насложи към текущия вектор на скоростта и тялото ще придобие нова скорост
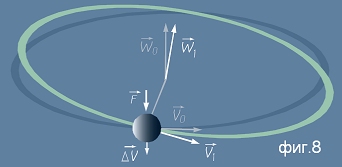
V1 - векторна сума на началната и придобитата скорост: 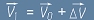 - виж фиг.8.
- виж фиг.8.
Заедно с линейната, ще се промени и ъгловата скорост - да означим новата ъглова скорост с W1.
Но по дефиниция от по-горе вектора на ъгловата скорост (и заедно с него оста на въртене) е насочен по права,
минаваща през центъра и перпендикулярна на линейната скорост. Ето защо
новата ос и новата ъглова скорост са вече други - виж бялата стрелка W1 на фиг.8. Ако съпоставим фиг.8 с
фиг.4, вече е ясно защо въртящият се диск реагира така "странно".
коментари
Радостин Желязков 27.08.2010 последна редакция 16.03.2013
________________________________________________________________________________________
учебни статии по физика
 Движение по окръжност
Движение по окръжност
 Да предположим, че едно тяло (материална точка) се движи с една и съща по големина скорост по окръжност.
Това означава, че има твърда връзка, която запазва разстоянието между разглежданата точка и центъра на окръжността.
По-долу ще предполагаме, че това разстояние е ненулево.
Добре е да уговорим и понятието ос на въртене - права, минаваща през центъра
и перпендикулярна на скоростта, с която се движи тялото.
Всички следващи определения са спрямо този център и ос.
Добре е също да уточним какво е дясна координатна система - това е такава
система координатни оси, че ако застанем в центъра и гледаме към първи квадрант/октант,
подредбата на осите ще се върти надясно (по часовниковата стрелка).
Тук ще подразбираме дясна координатна система.
Да предположим, че едно тяло (материална точка) се движи с една и съща по големина скорост по окръжност.
Това означава, че има твърда връзка, която запазва разстоянието между разглежданата точка и центъра на окръжността.
По-долу ще предполагаме, че това разстояние е ненулево.
Добре е да уговорим и понятието ос на въртене - права, минаваща през центъра
и перпендикулярна на скоростта, с която се движи тялото.
Всички следващи определения са спрямо този център и ос.
Добре е също да уточним какво е дясна координатна система - това е такава
система координатни оси, че ако застанем в центъра и гледаме към първи квадрант/октант,
подредбата на осите ще се върти надясно (по часовниковата стрелка).
Тук ще подразбираме дясна координатна система.
 (омега) - ъглова скорост;
(омега) - ъглова скорост; - линейна скорост;
- линейна скорост; - линейно ускорение;
- линейно ускорение; - ъглово ускорение;
- ъглово ускорение; - въртящ момент (момент на сила спрямо ос);
- въртящ момент (момент на сила спрямо ос); - момент на импулса;
- момент на импулса;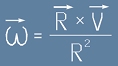 .
.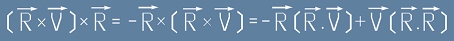 . Първото събираемо е нула, защото съдържа като множител скаларното произведение на два взаимно перпендикулярни
вектора R.V;
. Първото събираемо е нула, защото съдържа като множител скаларното произведение на два взаимно перпендикулярни
вектора R.V; [1].
[1].  Да разгледаме две точки A1 и B1 от движението, с радиус-вектори R1 и R2; Да означим скоростите с V1 и V2.
Да построим мислен вектор от B1 до A2, равен по посока и големина с V1.
Да разгледаме две точки A1 и B1 от движението, с радиус-вектори R1 и R2; Да означим скоростите с V1 и V2.
Да построим мислен вектор от B1 до A2, равен по посока и големина с V1.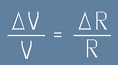 ,
,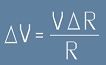 . Да разделим двете страни
на това равенство с интервала време между двете положения на точката:
. Да разделим двете страни
на това равенство с интервала време между двете положения на точката:
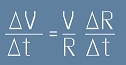 . При малки временни интервали клонящи към нула, лявата страна на това равенство
по дефиниция клони към ускорението, а последния множител клони към скоростта V. Така получихме оценка за големината
на ускорението:
. При малки временни интервали клонящи към нула, лявата страна на това равенство
по дефиниция клони към ускорението, а последния множител клони към скоростта V. Така получихме оценка за големината
на ускорението: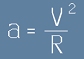 . Лесно е да съобразим, че като вектор
. Лесно е да съобразим, че като вектор 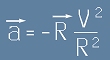 .
.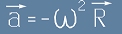 [2].
[2]. 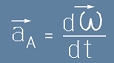 .
.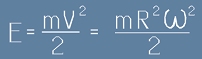 .
Енергията е скалар. Тук тя е само представена чрез ъгловата скорост, тоест това не е определение за енергия,
но е написано, защото подпомага следващото.
.
Енергията е скалар. Тук тя е само представена чрез ъгловата скорост, тоест това не е определение за енергия,
но е написано, защото подпомага следващото. се определя като Инерчен момент. Това е мярка за
инертността на въртящото се тяло, тя играе роля, подобна на масата (m) при постъпателно движение. От определението се
вижда, че мярката за инерчен момент е [килограм х метър х метър].
се определя като Инерчен момент. Това е мярка за
инертността на въртящото се тяло, тя играе роля, подобна на масата (m) при постъпателно движение. От определението се
вижда, че мярката за инерчен момент е [килограм х метър х метър].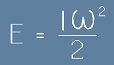 ,
което е подобие на равенството E=mv2/2.
,
което е подобие на равенството E=mv2/2. 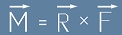
 [3],
[3],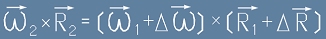 ,
а след разкриване на скобите равенството [3] ще изглежда така:
,
а след разкриване на скобите равенството [3] ще изглежда така: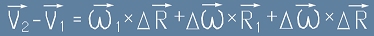 .
.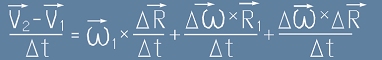 [4]
[4] , където векторът V е линейната скорост;
, където векторът V е линейната скорост;

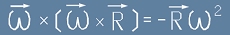 .
.
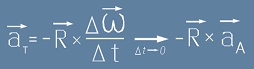 .
Двете съставки на ускорението от [4] съответствуват на две съставки в силата - радиална и допирателна.
Радиалната съставка е центростремителната сила.
.
Двете съставки на ускорението от [4] съответствуват на две съставки в силата - радиална и допирателна.
Радиалната съставка е центростремителната сила.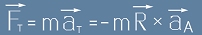 .
Ако умножим с отляво векторно с R двете страни, ще получим
.
Ако умножим с отляво векторно с R двете страни, ще получим 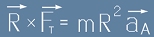 .
.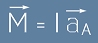 [6],
[6],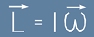 се определя като момент на импулса.
Това е аналог на импулса (p=mv) при постъпателно движение и се запазва във времето, освен ако въртящ момент не го промени.
Ако въртящият момент е нула, в дясно на [6] ще е нула ъгловото ускорение,
което означава постоянна ъглова скорост и постоянен момент на импулса.
се определя като момент на импулса.
Това е аналог на импулса (p=mv) при постъпателно движение и се запазва във времето, освен ако въртящ момент не го промени.
Ако въртящият момент е нула, в дясно на [6] ще е нула ъгловото ускорение,
което означава постоянна ъглова скорост и постоянен момент на импулса.
 Да си представим неподвижен метален диск, висящ в безтегловност и сила F,
която действува в периферията му перпендикулярно на плоскостта, за кратко време - нека смятаме това за удар - както е показано на фиг.1.
Да си представим неподвижен метален диск, висящ в безтегловност и сила F,
която действува в периферията му перпендикулярно на плоскостта, за кратко време - нека смятаме това за удар - както е показано на фиг.1.
 Нека сега си представим същия диск в безтегловност, но този път въртящ се около своята ос и следователно
имащ някакъв начален момент на импулса - вектор WP0. Да нанесем същия удар по периферията, както в по-горе,
в пример 1. - виж фиг.3
Нека сега си представим същия диск в безтегловност, но този път въртящ се около своята ос и следователно
имащ някакъв начален момент на импулса - вектор WP0. Да нанесем същия удар по периферията, както в по-горе,
в пример 1. - виж фиг.3
 Горния пример (2) може да се представи по-разбираемо, ако заменим диска с едно малко по размери тяло което се върти около
център - например е свързано с твърда нишка. Да означим с V0 линейната скорост в началото и с W0 - ъгловата скорост (фиг.5).
Да повторим удара от пример 1 със сила F действуваща върху тялото и перпендикулярна на плоскостта на въртене - виж фиг.6.
Горния пример (2) може да се представи по-разбираемо, ако заменим диска с едно малко по размери тяло което се върти около
център - например е свързано с твърда нишка. Да означим с V0 линейната скорост в началото и с W0 - ъгловата скорост (фиг.5).
Да повторим удара от пример 1 със сила F действуваща върху тялото и перпендикулярна на плоскостта на въртене - виж фиг.6.

 Силата F ще придаде на тялото ускорение и заедно с това промяна
Силата F ще придаде на тялото ускорение и заедно с това промяна -
виж фиг.7. Тази промяна ще се насложи към текущия вектор на скоростта и тялото ще придобие нова скорост
V1 - векторна сума на началната и придобитата скорост:
-
виж фиг.7. Тази промяна ще се насложи към текущия вектор на скоростта и тялото ще придобие нова скорост
V1 - векторна сума на началната и придобитата скорост: 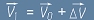 - виж фиг.8.
- виж фиг.8.