 Тяло хвърлено под ъгъл
Тяло хвърлено под ъгъл
Чисто геометрична постановка. Достатъчни са знания от средно училище.
Задача
Тяло (материална точка) е хвърлено под ъгъл спрямо хоризонта. Да се намери при какъв ъгъл тялото пада най-далеч.
Приемаме, че началната скорост е константа, означена по-долу с голяма буква V.
Няма въздух, размерът на тялото е нулев. Земното ускорение е постоянно, означено по-долу с малка буква g.
На Фиг.1 хоризонталната ос е по посоката на хвърляне.
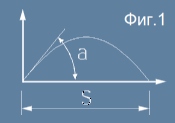
Да означим с малка буква а търсения ъгъл, с голяма буква S далечината на полета.
Тъй като двата определящи вектора-началната скорост и земното ускорение са постоянни и имат обща начална точка,
кривата лежи в равнина, определена от тях. Изобщо това е сбор от две едномерни движения
- едно в хоризонтално направление - равномерно и праволинейно плюс друго, във вертикално направление,
което е равноускорително с ускоренив g.
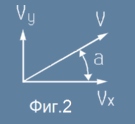
Началната скорост V е векторен сбор от хоризонтална и вертикална съставка Vx и Vy - Фиг.2.
При това големините на векторите Vx и Vy са:
 и
и  , [1]
, [1]
където V е големината на началната скорост. Нека полетът трае t секунди.
За хоризонталното движение важи 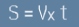 [2],
[2],
а за вертикалното 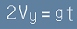 [3].
[3].
(Двойката е защото вертикалната съставка се променя веднъж от +Vy до нула и още веднъж от нула до -Vy.)
Да изразим времето от двете равенства [2] и [3]:
От [2] следва 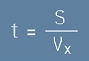 , а от [3] следва
, а от [3] следва 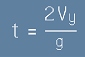 [4].
[4].
Това време - t - е едно и също за двете съставки на движението и десните страни на двете равенства [4]
трябва да са равни: 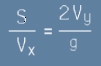 .[5]
.[5]
Ако вляво на равенството [5] трябва да остане само S, ще получим: 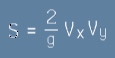 .[6]
.[6]
Да заместим [1] в [6]:  . [7]
. [7]
[Отклонение]:
Ще докажем, че 2 sin(a) cos(a) = sin (2a):
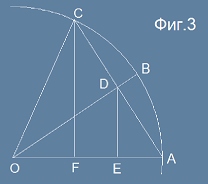
На Фиг.3 е изобразена част от окръжност с център О и радиус OA=1.
Нека дъгите AB и BC имат една и съща ъглова мярка, равна на нашият ъгъл а.
Очевидно отсечката OD е равна на cos(a), а отсечката DE е произведение OD*sin(a), тоест DE=cos(a)*sin(a).
Симетрията OB x AC показва, че триъгълникът ADE е два пъти по-малък от триъгълника ACF и значи
CF = 2 DE .
Но отсечката CF е точно равна на синус от ъгъла AOC=2a.
От тук следва твърдението sin(2a) = 2 sin(a) cos(a).
[Край на отклонението]:
Така, след [7], стигнахме до равенството 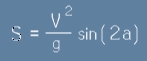 . [8]
. [8]
В дясната страна на [8] скоростта V и земното ускорение g са константи, променя се само ъгъл a.
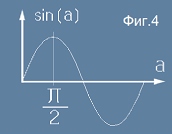
Синусовата крива има максимум при аргумент пи/2 (виж Фиг.4),
което означава, че максимална стойност за S от равенството [8] се наблюдава при аргумент на синуса 2a = пи/2.
Следователно максималната дължина S съответства на ъгъл a = пи/4.
Тоест ъгълът за най-далечно хвърляне е 45 градуса.
***
Добре е да напомним, че реалният начин, по който се движат хвърлените тела е чувствително различен
от простата постановка по-горе.
Това се дължи на неравномерната плътност на въздуха и щом има въздух, то форма, маса и размер на тялото имат значение.
Първото приближение за действителната траектория на хвърлено тяло в атмосфера се нарича балистична крива.
Радостин Желязков 04.06.2016
________________________________________________________________________________________
коментари
учебни статии по физика
 Тяло хвърлено под ъгъл
Тяло хвърлено под ъгъл


 и
и  , [1]
, [1]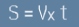 [2],
[2],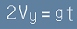 [3].
[3].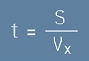 , а от [3] следва
, а от [3] следва 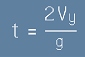 [4].
[4].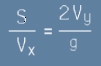 .[5]
.[5]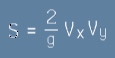 .[6]
.[6] . [7]
. [7]
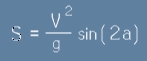 . [8]
. [8]