 Принцип на Хамилтон /принцип за най-малкото действие/
Принцип на Хамилтон /принцип за най-малкото действие/
Тази статия изисква познаване на
функцията на лагранж
, функции на две променливи и малко умения за
смятане с интеграли.
Те могат да бъдат намерени в
учебника по висша математика на Станчо Павлов.
 Действие
Действие
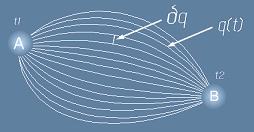
Нека A и B са начално и крайно състояние при движението на едно тяло в два момента t1 и t2.
Да означим с q(t) функцията на обобщените координати от времето. Да допуснем, че
има множество такива функции (траектории) и всички те имат еднакви стойности при t=t1 и при t=t2.
Да означим с L лагранжевата функция по една такава траектория q. Определеният интеграл на L по времето
от момент t1 до момент t2 се нарича действие - означено по долу с буква S.
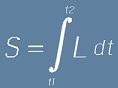
Смисъл
От механична гледна точка функцията L има размерност на енергия, тоест скалар.
Под интеграла има произведение на енергия по време, значи S също е скалар.
Числената стойност на S варира при различните траектории и колкото са по-близки две траектории,
толкова по-малка е вариацията на S.
Принципът на Хамилтон твърди, че за истинското движение S има минимална числена стойност.
Извод
Да означим с 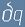 вариацията на траекторията и с
вариацията на траекторията и с  вариацията на действието.
(чете се делта q и делта S).
вариацията на действието.
(чете се делта q и делта S).
Екстремалната стойност на S означава, че  трябва е нула за малки вариации на q.
трябва е нула за малки вариации на q.
Лагранжевата функция 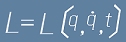 е функция на координати и скорости
(точка върху буква означава производна по времето).
е функция на координати и скорости
(точка върху буква означава производна по времето).
Вариацията на S се записва като интеграл по времето t1..t2:
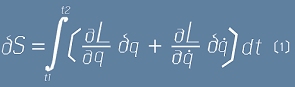 ,или като сбор
,или като сбор 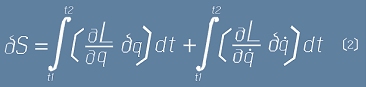
[отклонение 1]
Да забележим,че 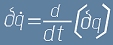 и по този начин е удобно да влезе под знака на диференциала.
и по този начин е удобно да влезе под знака на диференциала.
[/край на отклонение 1]
Второто събираемо от (2) може да се преобразува така:
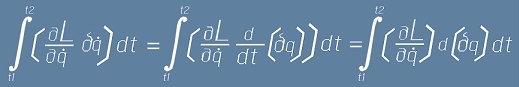 и след интегриране по части:
и след интегриране по части:
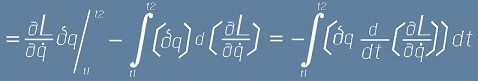 (Умаляемото е нула, защото вариацията на q е нула в моментите t1 и t2).
(Умаляемото е нула, защото вариацията на q е нула в моментите t1 и t2).
Сега да заместим последния интеграл обрано в (2):
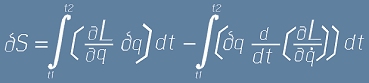 и в (1):
и в (1):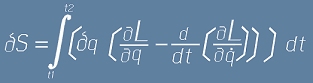
От тук се вижда, че за да е нулева вариацията на S, условието е:
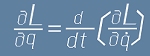 .
.
Радостин Желязков 05.07.2010
________________________________________________________________________________________
учебни статии по физика
 Принцип на Хамилтон /принцип за най-малкото действие/
Принцип на Хамилтон /принцип за най-малкото действие/
 Действие
Действие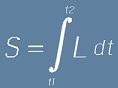
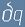 вариацията на траекторията и с
вариацията на траекторията и с  вариацията на действието.
(чете се делта q и делта S).
вариацията на действието.
(чете се делта q и делта S). трябва е нула за малки вариации на q.
трябва е нула за малки вариации на q.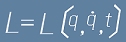 е функция на координати и скорости
(точка върху буква означава производна по времето).
е функция на координати и скорости
(точка върху буква означава производна по времето).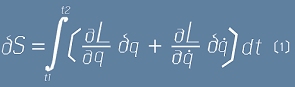 ,или като сбор
,или като сбор 
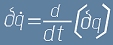 и по този начин е удобно да влезе под знака на диференциала.
и по този начин е удобно да влезе под знака на диференциала.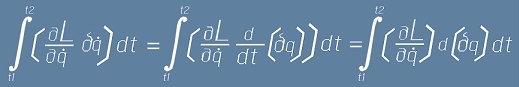 и след интегриране по части:
и след интегриране по части: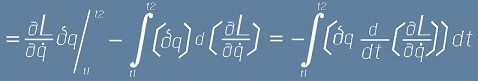 (Умаляемото е нула, защото вариацията на q е нула в моментите t1 и t2).
(Умаляемото е нула, защото вариацията на q е нула в моментите t1 и t2). и в (1):
и в (1):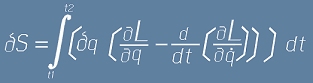
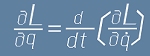 .
.