 Сферични координати
Сферични координати
Това е геометрична постановка. Достатъчни са знания от средно училище.
Лява и дясна координатна система
Координатните системи (К.С.) имат дясна или лява ориентация.
Погледнете илюстрацията (Фиг.1)
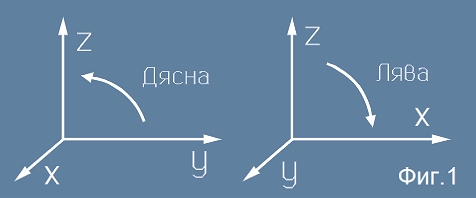
Там са показани дясна и лява координатни тройки оси (оста x от първата и оста y от втората са
насочени от рисунката навън, срещу зрителя). Ето една дефиниция, тоест
Определение:
Да застанем мислено в центъра на К.С.
Ако погледнем последователно в трите направления x,y,z и тази поредица е ляво завъртане
(обратно на часовниковата стрелка), то това е лява координатна система.
Връзка между сферични и правоъгълни координати
Нека двата ъгъла от сферичната К.С. са азимут - ъгъл, който се измерва от посоката север надясно
и височина - ъгъл над хоризонта. Да изберем посоката север да е по оста X, а посоката изток - Y. Z-оста е насочена нагоре.
Нека правоъгълните (декартовите) координати са x,y,z. Да означим сферичните координати с буквите a - азимут, b - височина, r - отстояние от центъра.
В такъв случай координатите a,b,r се получават от декартовите по следния начин:
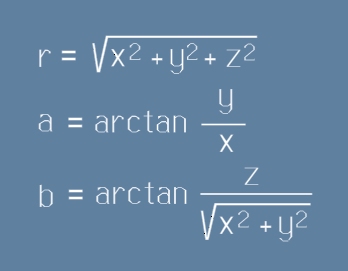
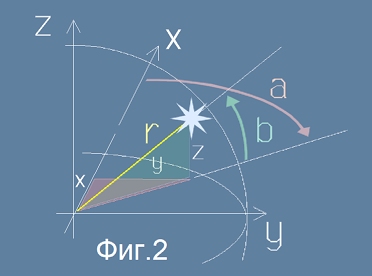
Горната рисунка (Фиг.2) показва начина, по който са получени тези формули. Координатната ос X е
насочена навътре в рисунката. Зеленият триъгълник лежи в отвесна плоскост, а червения - в хоризонталната
плоскост xy. Това са правоъгълни триъгълници и двата тангенса, от които се вземат
като аргументи ъглите (a и b) са видими отношения на катетите им. Жълтата отсечка е отстоянието (r)
до центъра, то е пресметнато по Питагорова теорема.
Сферичните координати често се наричат полярни координати. Преобразуването от полярни в декартови е:
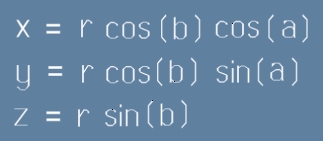
и то също е видимо от илюстрацията на Фиг.2
В полярна координатана система, ротация около z-оста е равносилна на прибавяне на ъгъл.
Но в правоъгълна к.с това не е така. Ето защо е добре да видим как изглежда в -
правоъгълна координатна система - една
Плоска ротация
Ако правоъгълната К.С. се завърти на фи градуса около Z-оста си, то xy координатите (на бялата точка в долните
схеми) ще се променят. Да разгледаме двете схеми Фиг.3 и Фиг.4:
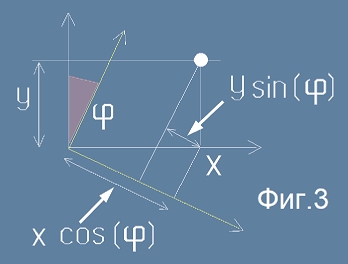
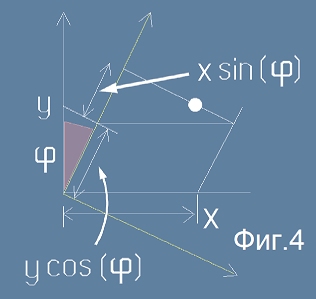
На тези схеми е изобразена лява координатна система (z-оста е навътре в рисунката), а ъгъл фи
се измерва като дясно въртене, тоест знака на ъгъла на завъртане е обратен на ориентацията на к.с.
Да означим с примове новите координати - x' и y'. От схемите виждаме, че новите координати
трябва да бъдат:
 [1]
[1]
Лесно в да съобразим, че ако ъгъл фи има същия знак както координатната система (тоест се върти в
другата посока - в ляво), то двете координати ще бъдат други:
 [2]
[2]
Координатни преходи
Горните преобразувания - полярно към плоско и ротациите са общоприети и се ползват
за преход от една към друга К.С. Нека припомним що за преходи са това.
Човек има удобно зрително поле, разположено пред него - зрителния конус е удобен в известен ъгъл,
да кажем 70 градуса по хоризонтално и около 40 градуса по вертикално направление. Да наречем това
обстановка за изследване.
Когато наблюдаваме някакъв предмет, се опитваме да застанем така, че предмета да попадне
именно в това зрително поле. Понякога можем с ръце да го поставим там. Но ако не можем,
заставаме на такова място, че да е в сила същата постановка.
В много случаи изследователя се пренася мислено на удобна позиция - за да се получи наречената
по-горе обстановка за изследване. Той винаги изгражда - понякога съзнателно, понякога не - своя
собствена координатна система, която е декартов тип - с координатни оси ляво/дясно, горе/долу,
напред/назад. Веднъж в този цикъл статии това беше наречено "тензорно преобразуване" - определящо
свойство за реалните предмети. Да идентифицираме реален предмет - това означава да разберем,
че този предмет се преобразува от неговата в нашата координатна система по тензорен начин.
Именно това прави наблюдателя, въртейки предмета в ръце, или когато сам обикаля около него.
Тензорно преобразуване - това е ротация, както изведената по-горе в [2] - зависимост
xy -> x'y'. В триизмерен случай това е xyz -> x'y'z'.
Сега да обърнем внимание на взаимното положение между наблюдател и предмет.
Често може бъде срещната фразата "външен наблюдател", която съответства на по-горе описаната
"обстановка за изследване". В такава обстановка са повечето геометрични рисунки.
На следващата картинка е изобразена полусфера, гледана отвън:
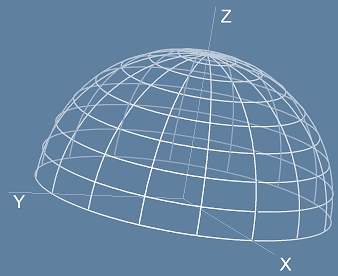
където са очертани географски паралели и меридиани - с цвят, който избледнява с разстоянието до
наблюдателя.
Но ние наблюдаваме небето не от вън, а от центъра на въображаемо кълбо, при което звездите са
"заковани" по свода му. Все едно да погледнем сферата от горната картинка, но заставайки в нейния
център. Тогава тя би изглеждала доста различно:

Втората картинка показва меридианите като прави линии (всеки голям кръг от централна гледна точка
изглежда като права), а паралелите - като елипси. В позицията на централен наблюдател всички
точки от сферата са на еднакво разстояние, затова цвета на линиите не се променя.
Чувствителна разлика между двата образа има в това, че зрителното поле на втората картинка е
несъразмерно голямо, тоест не спазва описаната по-горе обстановка за изследване.
Радостин Желязков 06.06.2019
________________________________________________________________________________________
коментари
учебни статии по физика
 Сферични координати
Сферични координати

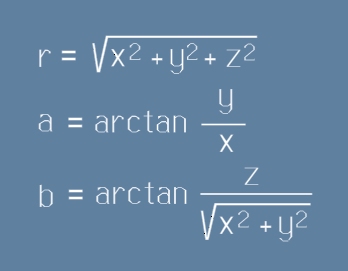

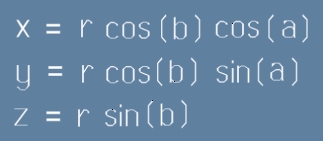


 [1]
[1] [2]
[2]
