 Сферични триъгълници
Сферични триъгълници
Това е геометрична постановка. Достатъчни са знания от средно училище.
Разгледани са само два сферични триъгълника - правоъгълен и равнобедрен.
Допирателни повърхности
Обикновените геометрични правила са удобни за ползване върху равнина, но не и върху
криви повърхности. Случаят със сферична повърхност е малко по-лесен за изследване от
произволна неплоска повърхност. Но във всички случаи ще ни е нужна помощна допирателна
плоскост към повърхността. По-долу има някои разсъждения относно триъгълник,
нарисуван върху повърхността на сфера.
Сферична повърхност
Улеснението при сферите е, че всяка точка от повърхността е на еднакво разстояние R от
центъра на сферата. Между две различни точки от сферата минава точно една голяма окръжност -
това е сечение на тази сфера с равнина, която минава през центъра на сферата.
Образуваната между две точки голяма дъга се измерва със своя централен ъгъл - това е ъгъл между
двата радиуса до тези две точки. Нека върху сферата има три точки, които не
лежат на една голяма окръжност. Това образува вече
Сферичен триъгълник
Трите дъги на сферичните триъгълници са всъщност техните централни ъгъли.
Но между всеки две дъги се образуват повърхностни ъгли. Повърхностният ъгъл -
това е ъгъл между допирателните прави към двете дъги в точката на пресичане.
Допирателната права лежи в същата плоскост, която е определена от голямата окръжност
на дъгата. От друга страна допирателната права е перпендикулярна на радиуса в тази точка.
Следователно повърхностният ъгъл между две дъги е всъщност ъгъл между плоскостите,
в които лежат тези две дъги. Ако един от трите повърхностни ъгъла е прав,
то това вече е
Сферичен правоъгълен триъгълник
Да разгледаме чертежа на Фиг.1
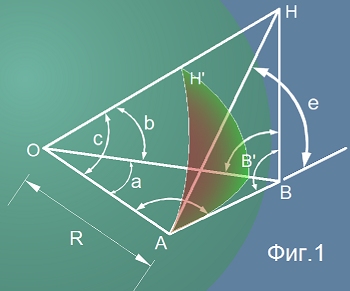
Сферата е зелена, а центъра на сферата е точка O. Сферичният триъгълник е от точките A B' H'.
Ъглите означени с малки букви a,b,c са централните ъгъли, тоест дъговите мерки за страните
на триъгълника. Интуитивно можем да предположим, че ако са известни трите централни ъгъла, то и повърхностните
ъгъли са определени от тях. Но как? Ще потърсим връзка между централни и повърхностни ъгли.
Нека повърхностния ъгъл A B' H' е прав. Да построим допирателна плоскост ABH към сферата в точка A. Заедно с
плоскостите от трите големи кръга, тази плоскост отсича фигурата - OABH - това е тетраедър,
за който са известни:
1. Една от страните OA=R;
2. Ъгъл OAB=90 градуса;
3. Ъгъл OAH=90 градуса;
(2 и 3 са защото радиуса OA е перпендикулярен на построената плоскост ABH и значи
е перпендикулярен на всяка права от тази плоскост)
Но ако повърхностния ъгъл AB'H' е прав, то прав е ъгъла между допирателните (в точка B') към дъгите AB' и B'H'.
Допирателната в точка B' към дъгата B'H' е перпендикулярна на радиуса OB' а също и на правата - допирателна
в точка B' към дъгата AB' - това значи, че тази допирателна е перпендикуляврна на плоскостта OAB и следователно
е успоредна на правата BH. (две прави, перпендикулярни към една и съща равнина са винаги успоредни)
От тук следва, че и ъгъл OBH също е прав. Прибавяме това равенство към горните три:
4. Ъгъл OBH=90 градуса;
Не е много трудно да преценим, че ABH също е прав ъгъл:
5. Ъгъл ABH=90 градуса;
В тетраедъра OABH получихме няколко удобни правоъгълни триъгълника, в които присъства търсената връзка
между повърхностни и централни ъгли. Ето как:
Нека означим с малка буква e повърхностния ъгъл в точка A. Този ъгъл е остър ъгъл в правоъгълния
триъгълник ABH. Да запишен тригонометричните съотношения:
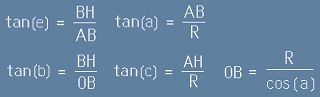 [1] и следователно
[1] и следователно 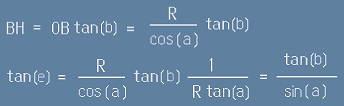 [2]
[2]
По същия обикновен начи виждаме, че
 [3]
[3]
От всичко това получихме двете важни равенства:
 [4]
[4]
В които е записана една връзка между централните ъгли (a,b,c) и един от повърхностните ъгли (e-този,
който е в допирателната точка A) в правоъгълния сферичен триъгълник.
Сферичен равнобедрен триъгълник
Известна е задачата за най-късия морски път - това е дъга от голям кръг върху сферичната повърхност
на океана. Без да решаваме най-общата постановка, нека приемем, че са известни географските
координати на началото и края на маршрута - две точки и че те лежат на един паралел. Ще потърсим
централния ъгъл за дъгата, която съответства на най-късия път. Да разгледаме долната
схема (Фиг.2) - там като H' и H'' са означени двете големи бели точки. Ако ги свържем с полюса
A, ще получим равнобедрен сферичен триъгълник A H' H", чиято основа H' H" - оранжевата отсечка
на схемата - е дъгата на най-късия път.
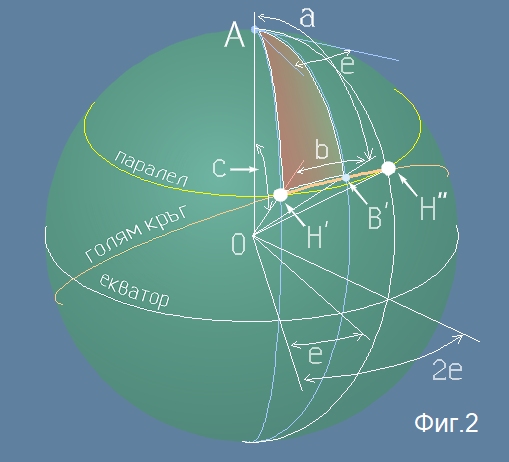
На схемата от Фиг.2 нарочно са спазени същите букви за точки и ъгли, които бяха използвани по-горе
в схемата на Фиг.1
Да разполвим триъгълника A H' H" на две части чрез един допълнителем меридиан A B', при което точка
B' е точно по средата на дъгата H' H". От симетрията се вижда, че този меридиан
е перпендикулярен на големия кръг, минаващ през двете точки H' и H" - защото ако два съседни ъгъла
са равни, то всеки от тях е прав.
Така се образува един сферичен правоъгълен триъгълник A B' H' (цветен на схемата). Този триъгълник
е равносилен на едноименния триъгълник AB'H' от Фиг.1 и за него важат изведените по-горе в [4]
съотношения. Дъгата B'H', която е половинката от търсения най-къс път е означената с малка
буква b на схемите по-горе.
Но на Фиг.1, както и в горния пример, ъгъл c (централен за дъгата AH') се измерва започвайки от
точка A (на Фиг.2 това е полюса), а в географията и астрономията, номерата на паралелите започват
от 0 градуса при екватора и стигат до +/- 90 градуса в двата полюса.
Така, че трябва да използваме не ъгъл c, а неговата добавка до 90 градуса (по-долу означена с w, така, че c = пи/2-w ).
Нека означим с m1 и m2 двата известни меридиана през H' и H". Тогава ъгълът между тях ще е 2e=(m2-m1), а ъгъл e -
повърхностният ъгъл прилежащ към A от триъгълника AB'H' ще бъде e=(m2-m1)/2 - това е ъгълът между
плоскостите на меридианите, минаващи през точка H' и точка B'.
Нека w - е номера на паралела, върху който лежат двете точки от маршрута.
Тогава ъгъл c ще бъде c=(п/2-w). Да запазим междинното означение a - тогава,
гледайки [4] пишем:
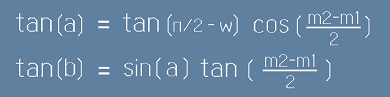 [5]
[5]
Където с буква b е означена половината от търсената дъга, представляваща най-късия път; С буква a - междинна променлива
за пресмятане (всъщност a е дъговата мярка за AB').
Не е зле да си спомним, че в статията "Успоредно пренасяне" имаше подобна обстановка свързана
с оценката за кривина.
Радостин Желязков 12.06.2019
________________________________________________________________________________________
коментари
учебни статии по физика
 Сферични триъгълници
Сферични триъгълници

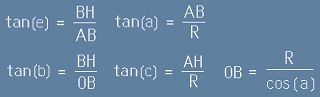 [1] и следователно
[1] и следователно 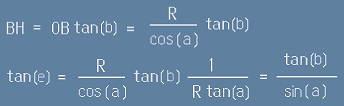 [2]
[2] [3]
[3] [4]
[4]
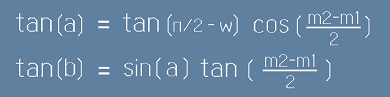 [5]
[5]