 Часовникът на Файнман
Часовникът на Файнман
Когато за първи път се запознах с часовника по-долу, това беше в книга на Ричард Файнман,
свързана със Специалната Теория на Относителността.
Изложението по-долу изисква малко знания по
интегрално смятане, достъпни чрез учебника на С.Павлов.
Въведение
Специалната Теория на Относителността е публикувана в 1905.
След като опита на Майкелсон-Морли показва, че ефирен вятър
не се долавя дори с точни методи на измерване, Айнщайн приема аксиоматично, че:
Първо, скоростта на светлината е константа - една и съща във
всички инерциални координатни системи и Второ, тя е недостижима.
Това внася неочаквана промяна в разбирането за движение, размер и време.
Оказва се, например, че за движещи се предмети с големи скорости времето и дължината се променят - стават по-малки.
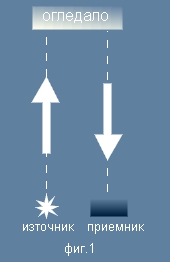
Часовникът
Да си представим часовник, който отмерва времето чрез светлинен
импулс - излъчван от източник, отразяван от огледало и на връщане
регистриран от приемник. - виж схемата на фиг.1. Да си представим, че хода на светлинния импулс е дълъг
и разстоянието между източника и приемника е пренебрежимо малко.
 При неподвижно състояние, времето между излъчването и приемането е 2T=2h/c,
където c е скоростта на светлината, T е времето за движение в една посока, h е разстоянието до огледалото,
а множителя 2 съответствува на двете части от хода на светлинния лъч.
Нека поставим този часовник на космически кораб, пътуващ отляво надясно със скорост v (фиг.2).
Единицата за време, която подвижният часовник ще отмерва е друга - t - чиято стойност,
съпоставена с неподвижното състояние води до равенството:
При неподвижно състояние, времето между излъчването и приемането е 2T=2h/c,
където c е скоростта на светлината, T е времето за движение в една посока, h е разстоянието до огледалото,
а множителя 2 съответствува на двете части от хода на светлинния лъч.
Нека поставим този часовник на космически кораб, пътуващ отляво надясно със скорост v (фиг.2).
Единицата за време, която подвижният часовник ще отмерва е друга - t - чиято стойност,
съпоставена с неподвижното състояние води до равенството:

така, че единицата време t в подвижната установка може да бъде изразена като:
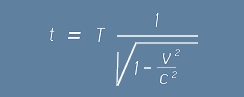
Тъй като t е по-голямо от неподвижната единица за време T, измерваното време в движещия се космически кораб ще е по-малко,
тоест времето ще тече по-бавно, отколкото за неподвижен наблюдател.
Дължина
След като приемем, че скоростта на светлината е константа,
естествена мярка за дължина би могла да е светлинната секунда.
Но както видяхме, секундата като време се променя при съпоставка от неподвижен към движещ се часовник.
Разумно е да очакваме, че и дължината ще се промени.
Единица дължина може да се изрази като

в неподвижна координатна система.
Ако вместо T запишем t като временен интервал от по-горния случай с часовника, това ще означава,
че измерваме движещата се дължина от неподвижна гледна точка:

Да разделим (2) на (1):
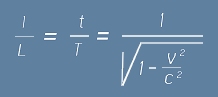
Тогава дължината l ще бъде изразена по подобен начин, както временния интервал t от по-горе:
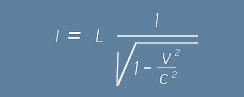
Тъй като дължината l (съответствуваща на мярка), е по-голяма от неподвижната мярка L, измерваната дължината на движещия се предмет е по-малка (скъсява се по направление на движението v).
Лоренцови преобразувания
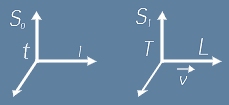
Да наречем своята координатна система S0, а тази ка кораба S1. Да си представим, че в точките (0,0,0) на S0 и S1 има монтирани часовници.
Да допуснем, че S1 се движи със скорост v по оста l на S0 и че трите координатни оси на двете системи са успоредни.
Нека в един момент началните точки на S0 и S1 съвпадат, а часовниците на двете координатни системи показват 0.
По нататък часовникът на кораба, както видяхме, ще показва друго време и неговите координати ще бъдат други.
Нека нашите координати и време са (l,t), а тези на кораба са (L,T).
Координатният преход от S0 към S1 се състои в двете функции l=l(L,T) и t=t(L,T).
Обратният преход - от S1 към S0 се състои в двете функции L=L(l,t) и T=T(l,t).
Тези два прехода трябва да са идентични.
След като знаем отношението на един временен интервал от S0 към S1, да допуснем,
че този интервал е бил достатъчно малък и че това отношение представлява диференциална промяна по T на функцията t=t(L,T).
Тогава функцията t(L,T) би трябвало да изглежда като неопределен интеграл:
 , където T0 е прибавка, независеща от T.
, където T0 е прибавка, независеща от T.
Аналогично:
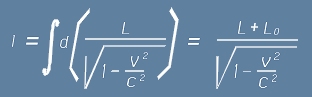 , където L0 е прибавка, независеща от L.
, където L0 е прибавка, независеща от L.
[Отклонение 1]
Да оценим двете свободни прибавки в получените формули:
Ако положим L=0 и решим последното уравнение, лесно се вижда, че 
Що се отнася до прибавката T0, ще трябва да положим T=0. Това означава да изпратим синхронизиращ импулс от S1 към S0,
с който по уговорка да занулим и часовника в S0. Импулсът ще пътува 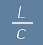 време.
Kоординатата на началото в S1 ще се отмести с
време.
Kоординатата на началото в S1 ще се отмести с 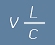 и това съответствува на временна разлика
и това съответствува на временна разлика 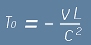 .
.
Двете равенства 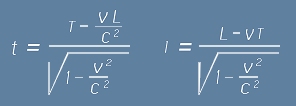 са известни още като преобразувания на Лоренц.
са известни още като преобразувания на Лоренц.
Исторически те са именувани така от Поанкаре.
В изданието "Обща и специална теория на относителността" Айнщайн ги представя в този вид.
[/край на отклонение 1]
[Отклонение 2]
Равенствата, наречени по-горе Лоренцови може да доведат до малко недоразумение.
Говорихме за преход от една координатна система в друга, но означихме с v скорост, която е спрямо
неподвижната координатна система S0. На тази скорост се полага да бъде вляво,
а ние я оставихме в дясната страна, тоест като аргумент не на място.
В дясно на двете равенства трябва да използуваме скорост от гледна точка на S1. Това означава да използуваме -v вместо v
и знаците на двете прибавки T0 и L0 ще се сменят, както и знаците в двата числителя.
[/край на отклонение 2]
Нека приемем, че примовите означения за координата, време (x' t') са в S1, а (x t) са в S0. В такъв случай получаваме:
 .
.
Събиране на скорости
Както по-горе се уговорихме, v е скоростта с която S0 се движи спрямо S1.
Нека едно тяло се движи със скорост w спрямо S0.
Да означим с 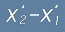 преместаването на това тяло в S1 между два момента време - пак в S1, различни с
преместаването на това тяло в S1 между два момента време - пак в S1, различни с
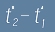 .
Относителната скорост в S1 на това преместване ще се изрази като:
.
Относителната скорост в S1 на това преместване ще се изрази като:
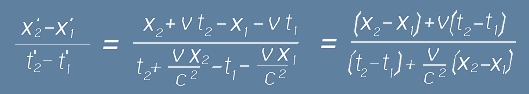 .
.
Ако разделим числителя и знаменателя с и приемем означението
и приемем означението
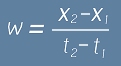 , получаваме
, получаваме
Правилото на Айнщайн за събирането на скорости:
Ако едно тяло се движи със скорост v , а друго тяло се движи със скорост w спрямо първото, резултантната скорост се
изразява с формулата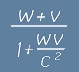 .
От тук се вижда, че резултантната скорост не превишава cкоростта на светлината c.
.
От тук се вижда, че резултантната скорост не превишава cкоростта на светлината c.
Радостин Желязков 12.08.2010
________________________________________________________________________________________
учебни статии по физика
 Часовникът на Файнман
Часовникът на Файнман

 При неподвижно състояние, времето между излъчването и приемането е 2T=2h/c,
където c е скоростта на светлината, T е времето за движение в една посока, h е разстоянието до огледалото,
а множителя 2 съответствува на двете части от хода на светлинния лъч.
Нека поставим този часовник на космически кораб, пътуващ отляво надясно със скорост v (фиг.2).
Единицата за време, която подвижният часовник ще отмерва е друга - t - чиято стойност,
съпоставена с неподвижното състояние води до равенството:
При неподвижно състояние, времето между излъчването и приемането е 2T=2h/c,
където c е скоростта на светлината, T е времето за движение в една посока, h е разстоянието до огледалото,
а множителя 2 съответствува на двете части от хода на светлинния лъч.
Нека поставим този часовник на космически кораб, пътуващ отляво надясно със скорост v (фиг.2).
Единицата за време, която подвижният часовник ще отмерва е друга - t - чиято стойност,
съпоставена с неподвижното състояние води до равенството:
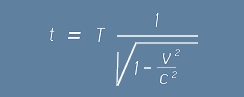


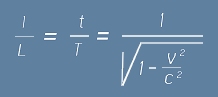
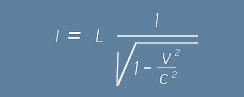

 , където T0 е прибавка, независеща от T.
, където T0 е прибавка, независеща от T. , където L0 е прибавка, независеща от L.
, където L0 е прибавка, независеща от L.
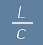 време.
Kоординатата на началото в S1 ще се отмести с
време.
Kоординатата на началото в S1 ще се отмести с 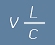 и това съответствува на временна разлика
и това съответствува на временна разлика 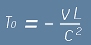 .
.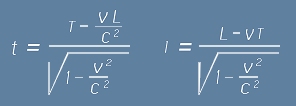 са известни още като преобразувания на Лоренц.
са известни още като преобразувания на Лоренц. .
.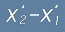 преместаването на това тяло в S1 между два момента време - пак в S1, различни с
преместаването на това тяло в S1 между два момента време - пак в S1, различни с
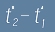 .
Относителната скорост в S1 на това преместване ще се изрази като:
.
Относителната скорост в S1 на това преместване ще се изрази като: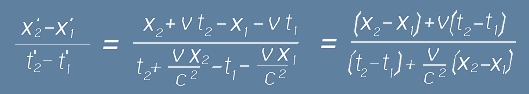 .
. и приемем означението
и приемем означението
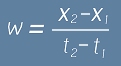 , получаваме
, получаваме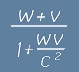 .
От тук се вижда, че резултантната скорост не превишава cкоростта на светлината c.
.
От тук се вижда, че резултантната скорост не превишава cкоростта на светлината c.