 Вълново Уравнение
Това е опростен модел на напречна вълна върху струна.
Вълново Уравнение
Това е опростен модел на напречна вълна върху струна.
Въведение
Предполагат се колебания с толкова малка амплитуда, че за всяка допирателна към кривата, сключваща ъгъл a с посоката x, cos(a)=1;
предполага се още, че струната не се деформира надлъжно и че линейната й плътност е постоянна.
Извод
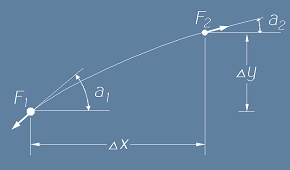

Да предположим, че формата на струната е функцията y(x,t). Да разгледаме малък участък между две близки точки.
Силите F1 и F2 действуват в двата края на участъка
под два различни ъгъла a1 и a2. Но при малки стойности на a1 и a2 и при липса на надлъжна деформация,
приемаме, че те са равни по големина:
F1 cos(a1) = F2 cos(a2) = F,
където F е силата на опън, една и съща по цялата струна. Да разложим F1 и F2 на вертикална и хоризонтална съставка.
Да запишем уравнението на Нютон за вертикалното ускорение, означавайки с m масата на разглеждания участък:
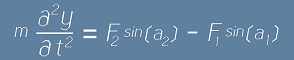 , където в дясно е вертикалната съставка на равнодействуващата сила.
Да разделим на F двете страни, като вземем предвид предположението от по-горе F1 cos(a1) = F2 cos(a2) = F:
, където в дясно е вертикалната съставка на равнодействуващата сила.
Да разделим на F двете страни, като вземем предвид предположението от по-горе F1 cos(a1) = F2 cos(a2) = F:
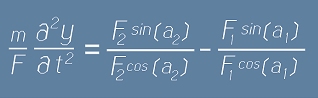 , което е равносилно на
, което е равносилно на
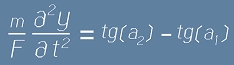 .
.
Но двата тангенса tg(a1) и tg(a2) са всъщност производните на функцията y(x) в двата края на разглеждания участък.
От друга страна, постоянната плътност позволява
в лявата част да заместим масата m с израз пропорционален на дължината на участъка:
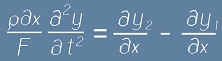 . Ако означим
. Ако означим 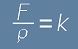 , получаваме
, получаваме
уравнението 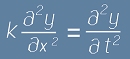 , наричано още Вълново Уравнение.
, наричано още Вълново Уравнение.
Радостин Желязков 14.08.2010
________________________________________________________________________________________
учебни статии по физика
 Вълново Уравнение
Това е опростен модел на напречна вълна върху струна.
Вълново Уравнение
Това е опростен модел на напречна вълна върху струна.


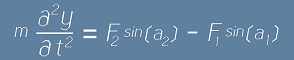 , където в дясно е вертикалната съставка на равнодействуващата сила.
Да разделим на F двете страни, като вземем предвид предположението от по-горе F1 cos(a1) = F2 cos(a2) = F:
, където в дясно е вертикалната съставка на равнодействуващата сила.
Да разделим на F двете страни, като вземем предвид предположението от по-горе F1 cos(a1) = F2 cos(a2) = F: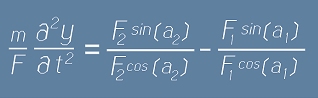 , което е равносилно на
, което е равносилно на
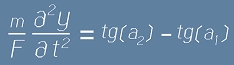 .
.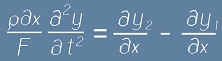 . Ако означим
. Ако означим 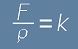 , получаваме
, получаваме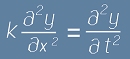 , наричано още Вълново Уравнение.
, наричано още Вълново Уравнение.