|
Версия вълнов вектор-координата
|
Обща версия
|
Да дефинираме аргумент k, който съединява в едно двата L и n:
|
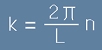 .[17] .[17]
|
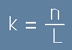 .[17.1] .[17.1]
|
|
Щом периодът на повторение е L, тогава 1/L ще е единицата честота - най-малката възможна.
|
Да означим ъгловата версия на тази единица с делта k:
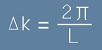 . [18] . [18]
|
Да означим единицата честота с делта k:
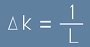 . [18.1] . [18.1]
|
Нека приемем, че извън интервала -L/2 .. L/2 функцията f(x) има пренебрежимо
малка стойност.
Тогава границите на интегриране в [15] могат да се разпрострат от минус до плюс безкрайност.
Така, че [15] и [16] биха изглеждали като
|
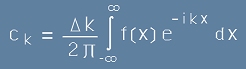 .[19] .[19]
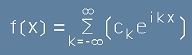 .[20] .[20]
|
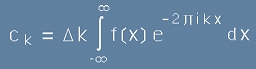 .[19.1] .[19.1]
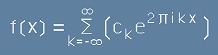 .[20.1] .[20.1]
|
Да приемем също означението
|
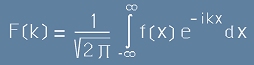 .[21] .[21]
|
 .[21.1] .[21.1]
|
Тогава коефициентите Ck ще бъдат:
|
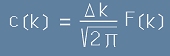 ,[22] ,[22]
|
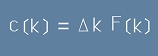 ,[22.1] ,[22.1]
|
a сборът [20] би трябвало да изглежда като
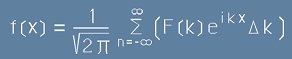 .[23] .[23]
|
a сборът [20.1] би трябвало да изглежда като
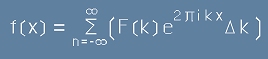 .[23.1] .[23.1]
|
Получихме сбор, който лесно се превръща в интеграл
при реална стойност на k.
|
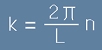 .[17]
.[17]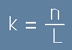 .[17.1]
.[17.1]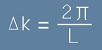 . [18]
. [18]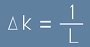 . [18.1]
. [18.1]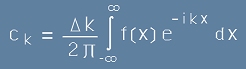 .[19]
.[19]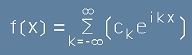 .[20]
.[20]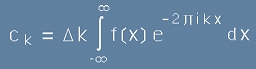 .[19.1]
.[19.1]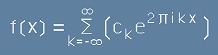 .[20.1]
.[20.1]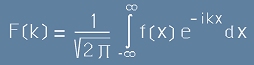 .[21]
.[21] .[21.1]
.[21.1]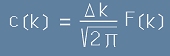 ,[22]
,[22]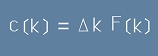 ,[22.1]
,[22.1]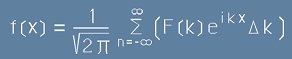 .[23]
.[23]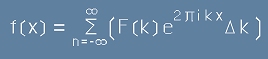 .[23.1]
.[23.1] Преобразувание на Фурие
Преобразувание на Фурие
 ..
..
 ).
). , [1]
, [1] . [2]
. [2]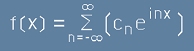 . [3]
. [3]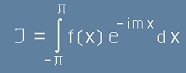 . [4]
. [4]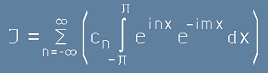 . [5]
. [5]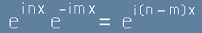 - той е равностоен на
- той е равностоен на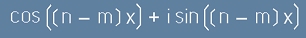 .[6]
.[6]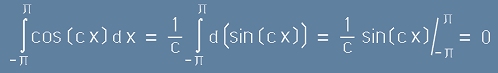 .[7]
.[7]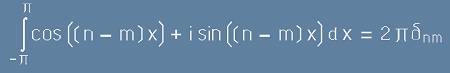 ,[8]
,[8]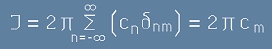 , тоест
, тоест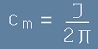 .[9]
.[9]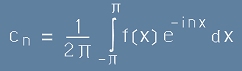 .[10]
.[10]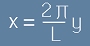 .[11]
.[11]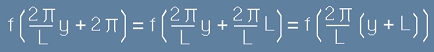 .[12]
.[12] ,[13]
,[13]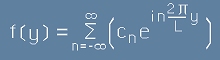 ,[14]
,[14]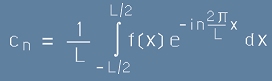 .[15]
.[15]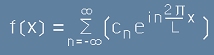 .[16]
.[16]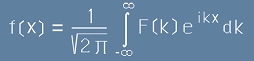 , [24]
, [24] , [24.1]
, [24.1]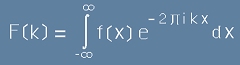 ." [25.1]
." [25.1]