 Дипол
Дипол
По-долу е дадено кратко описание на електричен дипол.
Направена е приблизителна оценка за големината на електричното поле от прости геометрични
съображения, без векторен анализ. Формата и посоката на полето е само илюстрирана с компютърен модел.
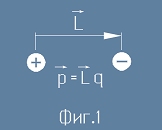 Диполът е двойка разноименни електрични точкови заряди с еднаква големина, разположени сравнително близко един до друг. (фиг.1)
Диполът е двойка разноименни електрични точкови заряди с еднаква големина, разположени сравнително близко един до друг. (фиг.1)
Ако разстоянието нежду двата заряда стане нула, общият заряд съсредоточен в тази точка ще е нулев,
както и полето, което те създават. В противен случай, сумарното им действие е модел,
с който се описват молекули, микрочастици, инженерни съоръжения - проводници, антени и др.
Ако с q означим големината на зарядите а с L означим вектора, който ги свързва, то вектора
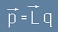 [1]
[1]
се смята за характеристика на дипола и се нарича
Диполен момент
Сам по себе си всеки заряд създава в пространството централно-симетрично поле
с интензитет обратно пропорционален на квадрата на разстоянието до заряда:
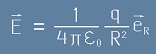 [2] ,
[2] ,
където с eR е означен единичен вектор в радиално направление.
Но ако в една точка има две полета, те имат независимо действие, така че резулатантното
поле е сбор, наречен
Суперпозиция
на двете полета. Ще направим оценка за характерните случаи. Да пресметнем полето в точка P, лежаща
на правата, която свързва двата заряда (фиг.2). Тази права се нарича
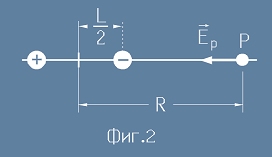
Полярна ос
или просто ос на дипола.
Средната точка между двата заряда се приема за център на дипола.
С буква R означаваме разстоянието от P до центъра,
така, че разстоянията от P до двата заряда са (R + L/2) и (R - L/2).
Сборното поле ще бъде
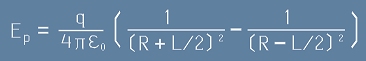 [3] .
[3] .
Индексът "p" за полето в лявата страна е за да напомня, че това важи за точки по полярната ос.
Да разгледаме само израза в големите скоби:
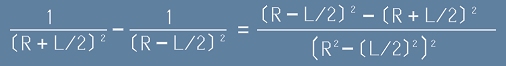
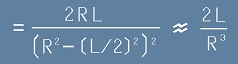 [4] ,
[4] ,
където приближението е за случаи в които R >> L , тоест разглежданата точка е на разстояние много по-голямо
от разстоянието L между двата заряда.
Да заместим [4] в [3] - получаваме  .
.
Да се възползуваме от дефиницията [1] (p=qL). Тогава полето е
 [5] ,
[5] ,
За точки по оста, на разстояния много по-големи от размера на дипола
(нарочно не съкратихме двойката от числителя, защото след малко ще ни трябва за съпоставка).
Равнината, която минава през центъра на дипола и е перпендикулярна на оста му се нарича
Екваториална равнина
Сега ще оценим действието на дипола върху точките в тази равнина.
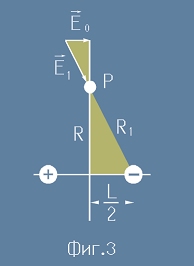
Нека точка P лежи в екваториалната плоскост (виж фиг.3).
Ще означим с Eq полето в тази точка.
Нека R е разстоянието до центъра на дипола. Векторът на полето в точка P е сбор от двете
полета. Вертикалните съставки на векторите от двете полета са противоположни и няма
да имат ефект. Обаче хоризонтаните (осевите) съставки се сумират и правят сборното поле - вектор успореден на оста.
Да пресметнем хоризонталната съставка E0 за полето, идващо от десния заряд.
От подобието на цветните триъгълници (фиг.3) се вижда отношението
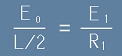 , тоест
, тоест
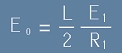 . [6]
. [6]
Тъй като 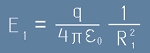 , получаваме
, получаваме
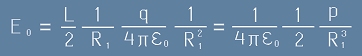 . [7]
. [7]
Това разбира се е само за половината от търсеното поле Eq. При условие, че R>>L, тоест
точка P се намира далеч от дипола, можем да смятаме, че R1=R
и тогава за екваториалното поле - удвоен израз [7] със заместено разстояние R вместо R1,
важи формулата
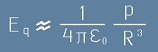 . [8]
. [8]
 Сметките в [8] и по-горе [5] показват три важни неща:
Сметките в [8] и по-горе [5] показват три важни неща:
Първо:
куба в знаменателя - полето отслабва с третата степен на разстоянието до дипола;
Второ:
несиметрия - полето по оста е двойно по-силно, отколкото по екватора;
Трето:
приблизителна вярност - за случай R>>L.
Моя компютърна програма, по формула [2] от по-горе построи рисунката
от фиг.4 - за суперпозицията на двете полета в
Близката околност
на дипола, без да са показани самите заряди.
Дължината на вектора за резултантното поле е по вертикално направление. Близко до всеки от зарядите се
образуват кладенци на безкрайно нарастване, тъй като в знаменателя на [2] присъствува квадрат на разстоянието до заряда.
Левият кладенец е с положителен знак, а десният - с отрицателен, както са знаците на зарядите.
След горните две оценки няма пречка да направим подобно пресмятане и за
Произволна точка
в пространството.
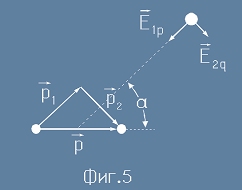 Диполният момент е вектор и с него можем да правим векторни сборове.
На фиг.5 диполният момент p е представен като векторен сбор от два взаимно перпендикулярни вектора p1 и p2.
Това ни позволява да разгледаме полето в произволна точка като сбор от едино чисто полярен
случай за съставката p1 и един чисто екваториален - за състaвката p2. Затова на фиг. 5 двете полета
са означени с E1p и E2q.
Тоест можем да смятаме, че E1=E1p и E2=E2q.
Дължината на векторния сбор
Диполният момент е вектор и с него можем да правим векторни сборове.
На фиг.5 диполният момент p е представен като векторен сбор от два взаимно перпендикулярни вектора p1 и p2.
Това ни позволява да разгледаме полето в произволна точка като сбор от едино чисто полярен
случай за съставката p1 и един чисто екваториален - за състaвката p2. Затова на фиг. 5 двете полета
са означени с E1p и E2q.
Тоест можем да смятаме, че E1=E1p и E2=E2q.
Дължината на векторния сбор
 при перпендикулярни събираеми се пресмята по Питагоровата теорема:
при перпендикулярни събираеми се пресмята по Питагоровата теорема:
 . [9]
. [9]
Като заместим двете полета от [8] и [5] в [9], получаваме
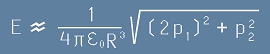 . [10]
. [10]
На фиг.5 с малка гръцка буква алфа е означен ъгълът между полярната ос и направлението от центъра
на дипола към разглежданата точка. Пак от там се вижда, че двата момента са
 и
и
 . Да ги заместим в [10]:
. Да ги заместим в [10]:
 . [11]
. [11]
Четирите косинуса под радикала са сбор от три плюс един, който заедно със синуса ще даде единица.
Ето как стигаме до обща формула за големината на полето от дипола, в каква да е точка:
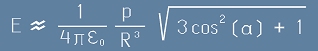 . [12]
. [12]
 Това потвърждава правилото, че полето на дипола е обратно пропорционално на третата степен на разстоянието
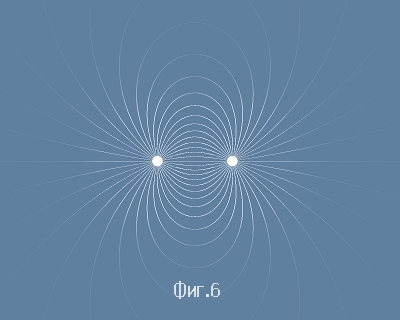
до центъра му. Написах програма, която проследява вектора на полето и тя състави рисунка (фиг.6) на
Това потвърждава правилото, че полето на дипола е обратно пропорционално на третата степен на разстоянието
до центъра му. Написах програма, която проследява вектора на полето и тя състави рисунка (фиг.6) на
Силовите линии
в непосредстена близост около двата заряда. Принципът на действие е : Избираме една точка, лежаща върху окръжност
с център първия заряд и радиус, доста по-малък от разстоянието между първия заряд и центъра.
Пресмятаме вектора на полето по формула [2]. Следващата точка я избираме по посока на така пресметнатия вектор
и стъпка по стъпка се движим по силовата линия - и заедно с това я рисуваме,
докато не попаднем върху втория заряд - край на силовата линия.
После започваме от друга точка върху същата окръжност, на разстояние 9 градуса от предишната
и правим следваща силова линия по същия начин. Рисунката на фиг.6 е съставна от 40 такива линии.
Цвета на линиите се опитва да спазва пропорция с големината на интензитета, тоест дължината на вектора
E на полето.
коментари
Радостин Желязков 12.04.2011
________________________________________________________________________________________
учебни статии по физика
 Дипол
Дипол
 Диполът е двойка разноименни електрични точкови заряди с еднаква големина, разположени сравнително близко един до друг. (фиг.1)
Диполът е двойка разноименни електрични точкови заряди с еднаква големина, разположени сравнително близко един до друг. (фиг.1)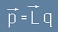 [1]
[1] 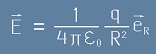 [2] ,
[2] ,
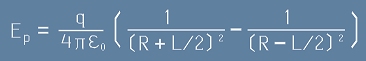 [3] .
[3] .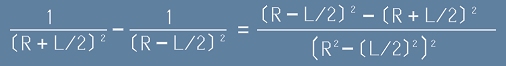
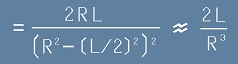 [4] ,
[4] , .
. [5] ,
[5] ,
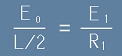 , тоест
, тоест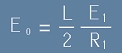 . [6]
. [6]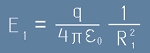 , получаваме
, получаваме
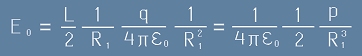 . [7]
. [7]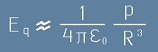 . [8]
. [8] Сметките в [8] и по-горе [5] показват три важни неща:
Сметките в [8] и по-горе [5] показват три важни неща: Диполният момент е вектор и с него можем да правим векторни сборове.
На фиг.5 диполният момент p е представен като векторен сбор от два взаимно перпендикулярни вектора p1 и p2.
Това ни позволява да разгледаме полето в произволна точка като сбор от едино чисто полярен
случай за съставката p1 и един чисто екваториален - за състaвката p2. Затова на фиг. 5 двете полета
са означени с E1p и E2q.
Тоест можем да смятаме, че E1=E1p и E2=E2q.
Дължината на векторния сбор
Диполният момент е вектор и с него можем да правим векторни сборове.
На фиг.5 диполният момент p е представен като векторен сбор от два взаимно перпендикулярни вектора p1 и p2.
Това ни позволява да разгледаме полето в произволна точка като сбор от едино чисто полярен
случай за съставката p1 и един чисто екваториален - за състaвката p2. Затова на фиг. 5 двете полета
са означени с E1p и E2q.
Тоест можем да смятаме, че E1=E1p и E2=E2q.
Дължината на векторния сбор
 при перпендикулярни събираеми се пресмята по Питагоровата теорема:
при перпендикулярни събираеми се пресмята по Питагоровата теорема: . [9]
. [9]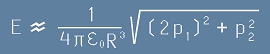 . [10]
. [10] и
и
 . Да ги заместим в [10]:
. Да ги заместим в [10]: . [11]
. [11]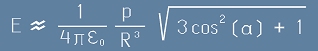 . [12]
. [12] Това потвърждава правилото, че полето на дипола е обратно пропорционално на третата степен на разстоянието
до центъра му. Написах програма, която проследява вектора на полето и тя състави рисунка (фиг.6) на
Това потвърждава правилото, че полето на дипола е обратно пропорционално на третата степен на разстоянието
до центъра му. Написах програма, която проследява вектора на полето и тя състави рисунка (фиг.6) на