 Планетарен модел на Ръдърфорд
Планетарен модел на Ръдърфорд
Тук е описан един от важните експерименти във физиката.
Направен е от Ернест Ръдърфорд през 1909.
Резултатите са публикувани във "Философско списание", брой 21 от 1911 г. в Манчестър.
Това е класически извод за явление, което от съвременна гледна точка би трябвало да се третира
като квантово.
По това време се е изграждала представата за атома.
Ръдърфорд получава Нобелова награда по химия за изобретяването на сцинтилоскопа -
уред, споменат по-долу, с който е възможно да се наблюдават отделни алфа-частици.
Изложението в тази статия е съвременно и технически, в известен смисъл, се отклонява от оригинала на Ръдърфорд.
Атомите имат строеж
Съвсем наскоро Дж.Дж.Томсън е открил електрона и е определил с добра точност
съотношението между масата и заряда му. Когато Томсън разбира, че тази частица е с маса,
хиляда пъти по-малка от водородния атом - най-малкия известен - става ясно,
че електронът трябва да е част от атома, тоест атомът не е неделим, а е съставен от по-малки части.
Дж.Дж. Томсън е автор на първото предположение за състава на атома - модел, наричан "сливов пудинг"
- според него, атомът е капка от положително заредена течност, в която плуват електрони.
Ръдърфорд прави описания по-долу експеримент с цел именно да сондира атома в дълбочина,
за да изясни строежа му.
Всъщност експеримента е правен от Гайгер и Мардсен - студенти на Ръдърдорд,
затова техните имена често се свързват с него.
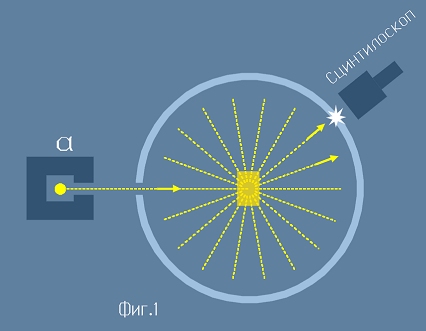
Опитна постановка
На фиг.1 е изобразена идеята в опита. В ляво е нарисуван схематично източник на
алфа-частици - оловна кутийка, в средата на която има радиоактивно вещество. От процепа
се излъчва сноп, насочен към пробно парче материал. За проба е била използувана
тънка златна пластинка - жълтия правоъгълник в центъра на големия кръг.
Ръдърфорд е знаел, че алфа-лъчите имат достатъчно висока енергия, за да пробият материала.
Ударите между алфа-частиците и атомите в златната пластинка водят до разсейване на алфа-лъчите.
Разсеяните частици са били наблюдавани като проблясъци с изобретението на Ръдърфорд -
сцинтилоскопа.
Гайгер и Мардсен са броили и записвали проблясъците за всяко ъглово деление по
екрана, изобразен на фиг.1 като голяма, светло синя окръжност.
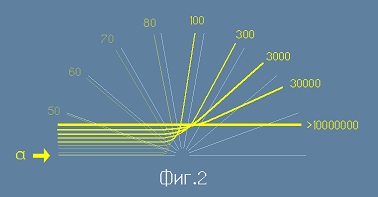
Резултат
Наблюденията показали, че преобладаващата част от частиците преминават безпрепятствено
през материята, но малка част от тях се отклоняват от праволинейната траектория,
като се разсейват не само на малки ъгли, но дори и в посока обратна на първоначалния поток.
Вероятността за отклонение рязко пада с ъгъла на разсейване.
Изобразената диаграма на Фиг.2 илюстрира характера
на постигнатите в опита резултати. Числата представляват броя алфа-частици, отклоняващи се при
взаимодействието на различен ъгъл.
Това е било изненадващо. Ако атомите бяха плътни образувания, както се е предполагало в пудинга на Томсън, разсейването
щеше да е на много малки ъгли около прицелното направление.
Но (по-долу е обяснено как) фактът, че някои частици се отклоняват значително, показва, че атомите са почти кухи
и цялата им маса, както и положителния заряд, е съсредоточен в малка централна област.
Така се поражда представата на Ръдърфорд за атома - малко ядро с размери
около 10-15 .. 10-14 метра и положителен заряд, около което,
на големи разстояния се намират електроните.
В публикацията на "Философско списание" от април 1911 г. Манчестър сити,
се споменава изразът "Сатурнов модел" - при който електроните кръжат в пръстен около ядрото.
Названието "Планетарен модел" се утвърждава по-късно, след работата Бор (1913).
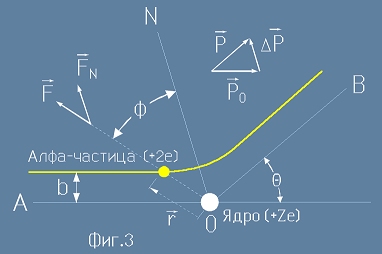
Поглед отблизо
На фиг.3 е показана с жълта линия движението на една алфа-частица. Алфа-частиците
имат електричен заряд +2e.
Зарядът на ядрото е означен като +Ze. Разстоянието b, на което би се доближила частицата до ядрото,
ако летеше по права, понякога се нарича параметър на удара, или прицелен параметър.
С гръцка буква Тита е означен ъгъла на отклонение (между крайния и началния вектор на скоростта).
Ключов момент в разбирането на експеримента е връзката между ъгъл Тита и параметъра b.
Правите AO и OB са успоредни на асимптотите на траекторията, която представлява хипербола
с ос N - ъглополовящата на ъгъл AOB.
Отблъскващата електрична сила от ядрото към алфа-частицата е означена с буква F,
но само съставката FN (проекцията на F върху N) променя посоката на полета,
тъй като допълващата (тоест тангенциалната) съставка е антисиметрична в двата клона
на хиперболата и нейният сборен ефект е нулев.
Ако с P0 означим началния импулс, а с P - крайния, е спазено векторното равенство:
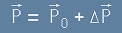 ,
,
където с делта P е означен вектора на промяната в импулса. По големина тази промяна е
 . [1]
. [1]
По време на движението, ъгълът означен на Фиг.3 с буква Ф, варира
от 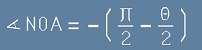 до
до
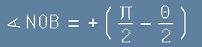 . [2]
. [2]
Да разгледаме движението на частицата спрямо център, съвпадащ с ядрото, като определено от
разстоянието до ядрото r и ъгъл Ф измерван
от N-направлението надясно.
Големината на ъгловата скорост, означена по-долу с омега е равна на
производната на централния ъгъл Ф по времето:
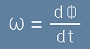 . [3]
. [3]
За големината на линейната скорост можем да запишем
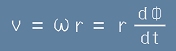 , [4]
, [4]
и за момента на импулса - означен с буква L:
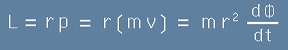 . [5]
. [5]
От друга страна, същото би трябвало да получим по формулата:
 , [6]
, [6]
където v0 е началната скорост на частицата.
Формула [6] се отличава от [5] само по възможното тълкуване,
но това няма значение, защото моментът на импулса не може да зависи от начина на разглеждане.
Десните страни на [5] и [6] трябва да са равни, значи
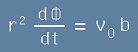 , тоест
, тоест
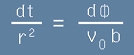 . [7]
. [7]
Последното равенство [7] ще бъде ползувано малко по-надолу.
Да се върнем към силата, причиняваща промяната в импулса.
Съгласно втория закон на Нютон, промяната в импулса се изразява като интеграл
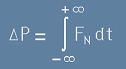 , [8]
, [8]
където FN е проекцията на кулоновата сила F върху оста N:
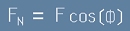 . [9]
. [9]
Заместваме [9] в [8], също и формулата на Кулон според казаното по-горе за зарядите на ядрото и алфа-частицата:
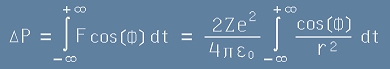 . [10]
. [10]
Да заместим [7] в [10] и да поставим като граници на определения интеграл вариращият ъгъл Ф:
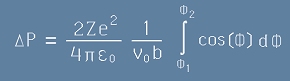 . [11]
. [11]
Съгласно установените по-горе в [2] граници за ъгъл Ф, можем да изразим интеграла от [11] като:
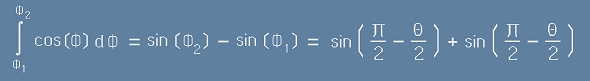 , или по-кратко
, или по-кратко
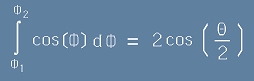 . [12]
. [12]
И така, вместо [11], изразът за промяната на импулса остава
 . [13]
. [13]
Да съпоставим дясната страна на последното равенство [13] с дясната страна на [1] от по-горе.
Ще получим равенството:
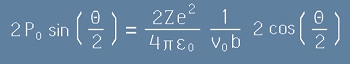 , [14]
, [14]
откъдето следва търсената връзка на параметъра b с ъгъла на отклонение Тита:
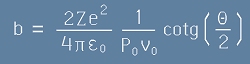 . [15]
. [15]
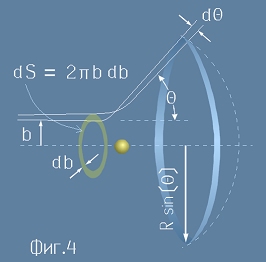
Оценка
Да направим мислено напречен разрез на алфа-снопа и да приемем, че цялото му сечение има
повърхност S. На Фиг.4 е изобразена пръстеновидна област от такова сечение,
за която параметъра b е постоянен. Площта на тази област е dS = 2пb db.
Да означим с n броя златни атоми в единица обем и с D дебелината на златната пластинка.
Броят на всички златни атоми, разсейващи снопа ще е N = n.D.S
Броят на атомите, попадащи в пръстена ще е dN=N.dS/S
Това представлява част от целия поток, изразена чрез:
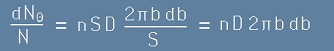 , [16]
, [16]
като индекса Тита в ляво на dN напомня, че това ще са удари, водещи до отклонение Тита.
Да пресметнем диференциала db чрез [15]:
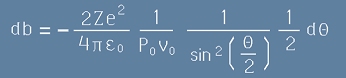 , [17]
, [17]
и да заместим [15] и [17] в [16]:
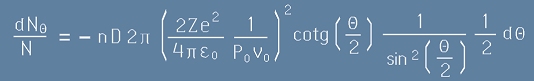 . [18]
. [18]
Да вземем предвид, че
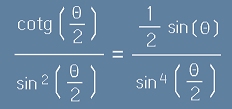 . [19.1]
. [19.1]
Да вземем предвид също, че  , [19.2]
, [19.2]
където буква E означава кинетичната енергия на алфа-частицата.
Да заместим [19.1] и [19.2] в [18]:
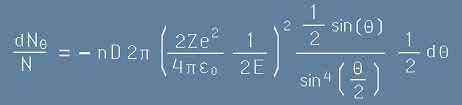 . [20]
. [20]
Знакът минус отразява факта, че при нарастване на b-параметъра, ъгълът на разсейване намалява.
Сега нека разгледаме сферичния сегментен пръстен, оцветен в синьо на Фиг.4, в който попадат алфа-частиците.
Този пръстен има площ
 , [21]
, [21]
където с R е означен радиуса на сферата.
Отношението на горната площ от [21] към квадрата на радиуса дава пространствения ъгъл:
 . [22]
. [22]
Формула на Ръдърфорд
Това е формула за разсейването на алфа-частиците по пространствен ъгъл.
Думата "разсейване" е мой превод (за целите на този текст) от анлийската "scattering"
(букв. разпръскване, разпиляване).
Разсейването на Ръдърфорд се означава обикновено с 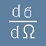 и показва каква част от алфа потока попада в единица пространствен ъгъл.
и показва каква част от алфа потока попада в единица пространствен ъгъл.
Ако го умножим по ъглъла от [22], ще получим потока на всички тита-отклонени частици от [20]:
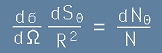 . [23]
. [23]
Решението на уравнението [23] спрямо разсейването (с помощтта на [22] и [20]), дава обещаната формула на Ръдърфорд:
 . [24]
. [24]
Именно този резултат - обратната пропорционалност на четвъртата степен на синус от половин тита,
е бил потвърден от опита.
коментари
Радостин Желязков 14.08.2011
________________________________________________________________________________________
учебни статии по физика
 Планетарен модел на Ръдърфорд
Планетарен модел на Ръдърфорд



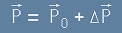 ,
, . [1]
. [1]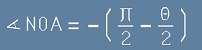 до
до
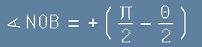 . [2]
. [2]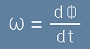 . [3]
. [3]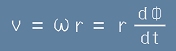 , [4]
, [4]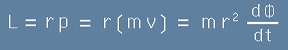 . [5]
. [5] , [6]
, [6]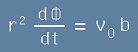 , тоест
, тоест
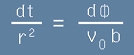 . [7]
. [7] 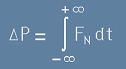 , [8]
, [8]  . [9]
. [9] 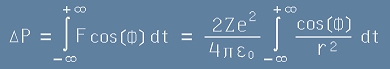 . [10]
. [10] 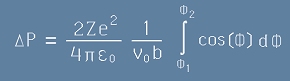 . [11]
. [11] 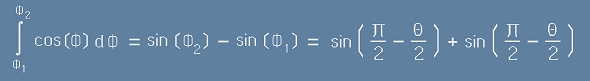 , или по-кратко
, или по-кратко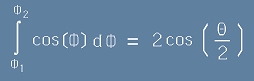 . [12]
. [12] . [13]
. [13]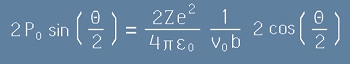 , [14]
, [14]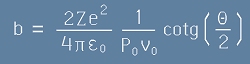 . [15]
. [15]
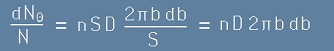 , [16]
, [16] , [17]
, [17]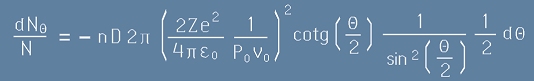 . [18]
. [18]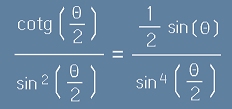 . [19.1]
. [19.1] , [19.2]
, [19.2]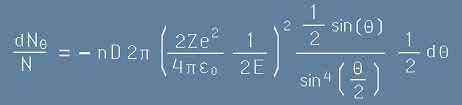 . [20]
. [20] , [21]
, [21] . [22]
. [22] и показва каква част от алфа потока попада в единица пространствен ъгъл.
и показва каква част от алфа потока попада в единица пространствен ъгъл.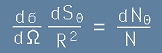 . [23]
. [23] . [24]
. [24]