 Гаусови интеграли
Гаусови интеграли
Тук са пресметнати Гаусовите интеграли едно, нула, две, четири (I1, I0, I2, I4).
Други статии се обръщат към тези интеграли за справка.
Гаусов интеграл с индекс m е 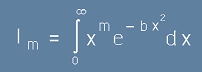 при m=0,1,2...
при m=0,1,2...
По-долу те са представени при отместен параметър a2=b.
Интеграл едно
Той е лесен за решаване :
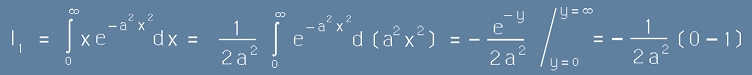 , или кратко
, или кратко
 . [1]
. [1]
* * *
Интеграл нула
Интегралът I0 изглежда така:
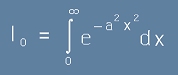 .
.
Пресмята се всъщност неговият квадрат.
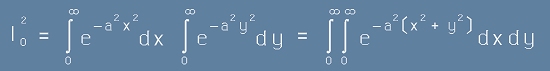 .
.
Квадрата на I0 покрива първи квадрант от декартова координатна система.
Правим преход към полярни координати:
 ,
,
заменяме декартовия повърхностен елемент с полярен:
 .
.
Нагласяме границите в полярния интеграл като за първи квадрант :
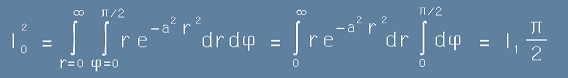 .
.
Заместваме I1 от [1] и за I0 остава:
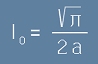 . [2]
. [2]
* * *
Интеграл две
Интегралът I2 изглежда така:
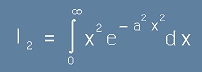 .
.
Ако положим b=a2, Интеграл нула от по-горе (виж [2]) се записва като
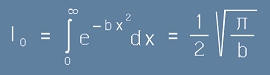 , [3]
, [3]
а I2, се превръща в
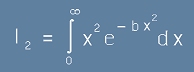 .
.
Той се представя като производна на [3] по параметъра b :
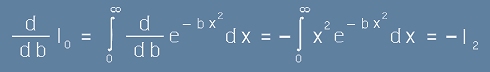 . [4]
. [4]
Имайки предвид [2], извършваме действието в [4]
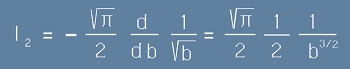
След като заместим обратно b=a2,
оконачтелно за интеграл две получаваме :
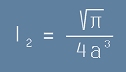 . [5]
. [5]
* * *
Интеграл четири
Всички четни индекси се получават по начин подобен на I2.
Производната I2 по b води до индекс 4:
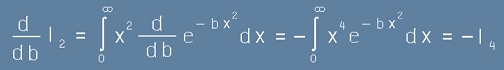 .
.
Пресмятаме я:
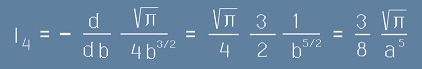 .
.
коментари
Радостин Желязков 01.05.2011 / последна редакция 11.07.2013
________________________________________________________________________________________
учебни статии по физика
 Гаусови интеграли
Гаусови интеграли
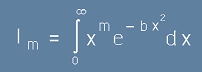 при m=0,1,2...
при m=0,1,2...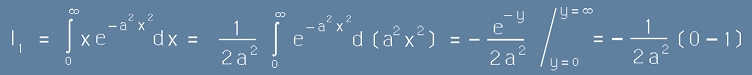 , или кратко
, или кратко . [1]
. [1]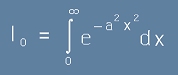 .
. 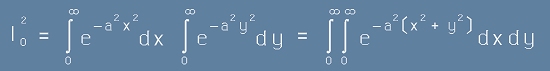 .
.  ,
, .
.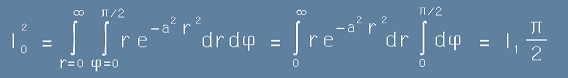 .
.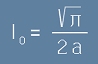 . [2]
. [2]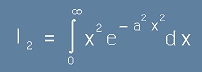 .
. 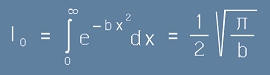 , [3]
, [3]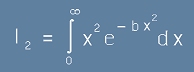 .
. 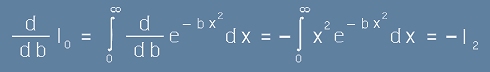 . [4]
. [4]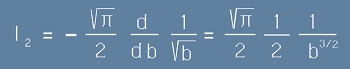
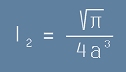 . [5]
. [5]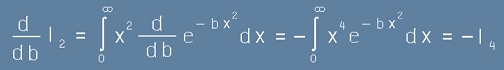 .
. 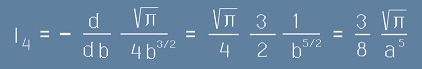 .
.