 Трептящ кръг
Трептящ кръг
Тук се тълкува на значението на фразата "периодичен процес".
Казано е какво е уравнение на хармоничен осцилатор как то е свързано с елетротехническия трептящ кръг.
Добре е да сте запознати с материала на Станчо Павлов
Формула на Ойлер.
 Думата период
Думата период
идва при нас от древногръцки. Буквално се превежда на Български език като "обход", "заход".
Смисълът е движение по периметъра, заобикаляне.
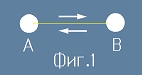
Един процес се определя като периодичен, ако след известно време се оказва
в началното си състояние. Едномерният случай на такъв процес е отиване
от точка A до точка B и връщане обратно (фиг.1).
 Като физично понятие периодът е време,
след което се възстановява началното състояние.
Като физично понятие периодът е време,
след което се възстановява началното състояние.
При движение на материална точка, "Да се върне в начално състояние" означава
да се окаже в същата позиция - тоест координата (и същата скорост), от която е започнало движението.
 На фиг.2 това е изобразено в координатна система t/x.
В най-простия случай движението би трябвало да е с постоянна скорост (производна по времето),
затова жълтата линия е права. Но в точката B, където тялото придобива
обратна по посока скорост се случва нещо неестествено - ъгъл, който
изражда графиката на движение в пречупена линия.
На фиг.2 това е изобразено в координатна система t/x.
В най-простия случай движението би трябвало да е с постоянна скорост (производна по времето),
затова жълтата линия е права. Но в точката B, където тялото придобива
обратна по посока скорост се случва нещо неестествено - ъгъл, който
изражда графиката на движение в пречупена линия.
Неестествено, защото първата производна по времето
не е достатъчна, за да опише периодичен процес.
Равномерно праволинейно движение не може да доведе движещото се тяло до началната му точка.
Освен това, в природата ъгли "няма". Непрекъснатостта интуитивно предполага,
че скоростта плавно пада до нула и после нараства в друга посока,
както е подчертано на фиг.2.
Пак от фиг.2 се вижда, че движението на това място се представя с крива.
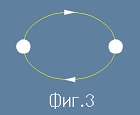
Геометричният примитив за крива е окръжност или елипса - израз от втора степен (фиг.3).
Ето как периодиката се асоциира с движение по затворена крива, тоест цикъл.
Именно времето за което се извършва цикъла се означава с T и се нарича Период. Както виждаме,
периодичното движение изисква променлива скорост.
Промяната в скоростта е всъщност втора производна на координатата по времето и се определя като
Ускорение
Следователно математическият израз който описва периодично движение трябва да съдържа
втора производна на координатата по времето.
Но за да се завърне тялото там, откъдето е тръгнало е нужна сила, действуваща в посока към началната точка.
В едномерния случай силата трябва да нараства с координатата, но с противоположен знак, например
 . [1]
. [1]
Известно равенство, в което участвуват ускорение и сила е формулата на Нютон
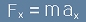 , [2].
, [2].
С него, приемайки [1], можем да напишем уравнението:
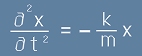 , [3]
, [3]
Да оценим коефициента k/m.
В ляво размерността е метър/секунда2.
Отдясно x е в метри. Излиза, че k/m трябва да има размерност единица/секунда2.
Честотата се измерва с единица/секунда. Всъщност коефициентът k/m представлява честота на квадрат и
най-често [3] се записва още като известното
Уравнение на хармоничния осцилатор
При функция x=x(t) - не непременно дължина, то изглежда така:
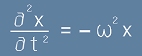 . [4]
. [4]
С малка гръцка буква омега е означена честота, по-точно брой цикли в секунда умножени по 2пи, тоест
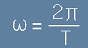 .
.
Множителят 2пи е за съвместимост с тригонометричните синус/косинус функции (виж по-долу). Но да потърсим
Решение
Каква би била функцията x=x(t), която удовлетворява уравнението [4]?
Ще опитаме по метода "предположи" и "провери".
Да предположим, че функцията е комплексна
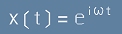 ,
където i е имагинерната единица. Да проверим. Първата производна е
,
където i е имагинерната единица. Да проверим. Първата производна е
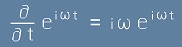 , а втората
, а втората
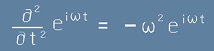 .
.
Съпоставката с [4] показва, че това действително е решение.
Не е трудно да проверим, че функцията
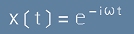 също е решение на [4].
също е решение на [4].
Видът на [4] ни подсказва, че функцията x(t) може да бъде умножена с константа и ще остане решение.
Сбор от две решения - също. Даже
произволна линейна комбинация от решения е също решение.
В частност формулите на Ойлер за представянето на тригонометричните функции (има линк по-горе, в началото):
 и
и 
са решения на [4]. Решение е и тяхната линейна комбинация
 , [5]
, [5]
където As и Ac са константи. Ето как хармоничните трептения се описват от синусови и косинусови функции.
* * *
Двойка уравнения като [1] и [2] се срещат повече от веднъж във физиката.
Разбира се пример номер едно е
Законът на Хук
Той е всъщност изразен с [1]: Еластичната сила Fx е право пропорционална на деформацията x.
Ако една еластична пластинка (пружина) бъде деформирана и отпусната в неравновесна позиция,
ще възникнат периодични колебания, тоест ще е налице хармоничен осцилатор, описван от уравнението [4].
Пример номер две за аналогична двойка равенства от горния тип [1] и [2] се намира в електромагнитния
Трептящ кръг
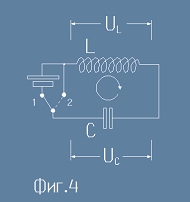 Да допуснем, че веригата на фиг.4 е в равновесие: Това значи, че кондензаторът е зареден
до напрежението на източника и токът е нулев.
Ако завъртим ключа в положение 2 (пунктирната линия), по веригата ще протече ток.
Този ток е всъщност скоростта, с която намалява заряда в кондензатора:
Да допуснем, че веригата на фиг.4 е в равновесие: Това значи, че кондензаторът е зареден
до напрежението на източника и токът е нулев.
Ако завъртим ключа в положение 2 (пунктирната линия), по веригата ще протече ток.
Този ток е всъщност скоростта, с която намалява заряда в кондензатора:
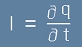 , [6]
, [6]
Очевидно токът няма да е постоянен, тъй като заедно с намаляване на заряда, ще намалява и напрежението.
Когато токът се променя, това е производна на [6] по времето:
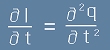 . [7]
. [7]
Променливият ток индуцира напрежение в намотката L по правилото
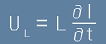 , [8]
, [8]
От [8] и [7] се вижда, че
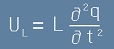 . [9]
. [9]
За кондензатора - с капацитет C - винаги е валидно отношението
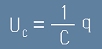 . [10]
. [10]
Но краищата на индуктивността L и кондензатора C са свързани, така, че
веригата е затворена и за нея важи правилото на Кирхоф - сбора от всички падове на напрежение е нулев:
 . [11]
. [11]
Сега ако погледнем двойката уравнения [10] и [9], и имайки предвид [11], можем да ги уподобим на [1] и [2] от по-горе.
Това веднага води до уравнение, аналог на [3] и [4]:
 , [12]
, [12]
което е уравнение на хармоничен осцилатор, при ъглова честота, определена от равенството
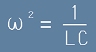 . [13]
. [13]
В общия случай, в такава система ще възникнат свободни хармонични трептения.
При описанието по-горе не е взето предвид топлинното действие на протичащия ток.
Но обикновено такова има и трептенията затихват - по аналогичен начин,
както колебанията в пружина или махало.
коментари
Радостин Желязков 14.04.2011
________________________________________________________________________________________
учебни статии по физика
 Трептящ кръг
Трептящ кръг
 Думата период
Думата период Като физично понятие периодът е време,
след което се възстановява началното състояние.
Като физично понятие периодът е време,
след което се възстановява началното състояние. На фиг.2 това е изобразено в координатна система t/x.
В най-простия случай движението би трябвало да е с постоянна скорост (производна по времето),
затова жълтата линия е права. Но в точката B, където тялото придобива
обратна по посока скорост се случва нещо неестествено - ъгъл, който
изражда графиката на движение в пречупена линия.
На фиг.2 това е изобразено в координатна система t/x.
В най-простия случай движението би трябвало да е с постоянна скорост (производна по времето),
затова жълтата линия е права. Но в точката B, където тялото придобива
обратна по посока скорост се случва нещо неестествено - ъгъл, който
изражда графиката на движение в пречупена линия.  . [1]
. [1]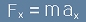 , [2].
, [2].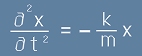 , [3]
, [3]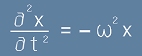 . [4]
. [4]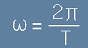 .
.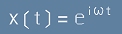 ,
където i е имагинерната единица. Да проверим. Първата производна е
,
където i е имагинерната единица. Да проверим. Първата производна е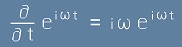 , а втората
, а втората
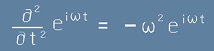 .
.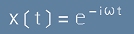 също е решение на [4].
също е решение на [4]. и
и 
 , [5]
, [5] Да допуснем, че веригата на фиг.4 е в равновесие: Това значи, че кондензаторът е зареден
до напрежението на източника и токът е нулев.
Ако завъртим ключа в положение 2 (пунктирната линия), по веригата ще протече ток.
Този ток е всъщност скоростта, с която намалява заряда в кондензатора:
Да допуснем, че веригата на фиг.4 е в равновесие: Това значи, че кондензаторът е зареден
до напрежението на източника и токът е нулев.
Ако завъртим ключа в положение 2 (пунктирната линия), по веригата ще протече ток.
Този ток е всъщност скоростта, с която намалява заряда в кондензатора: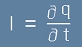 , [6]
, [6]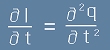 . [7]
. [7]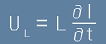 , [8]
, [8]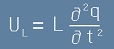 . [9]
. [9]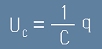 . [10]
. [10] . [11]
. [11] , [12]
, [12]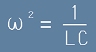 . [13]
. [13]