Малко за Питагор
Моят приятел Станчо ми каза следното доказателство за
неспособността на рационалните числа да опишат цялата
числова ос. Това доказателство, според Станчо е дадено от
Питагор. Аз го пресъздавам така, както го чух от Станчо и го
запомних, защото по общо мнение то е една красива класика.
То доказва че корен квадратен от 2 не е рационално число.
Питагор е забелязал че квадратите на четните числа са четни,
както и обратното - ако квадрата е четен, то и числото е четно.
Когато потърсим образа на числото корен квадратен от 2,
лесно се показва, че то лежи в интервала 1..2
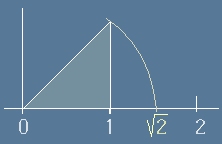 - то е дължина на хипотенуза в правоъгълен триъгълник с катети 1.
Да означим числото корен квадратен от 2 с буквата P
и да допуснем, че P е рационално число.
Всяко рационално число може да се запише като отношение на
две цели числа A/B, които нямат общ делител и представляват
несъкратима дроб. Значи поне едно от двете числа A и B
трябва да е нечетно. Сега да допуснем, че има такива числа и да
запишем
- то е дължина на хипотенуза в правоъгълен триъгълник с катети 1.
Да означим числото корен квадратен от 2 с буквата P
и да допуснем, че P е рационално число.
Всяко рационално число може да се запише като отношение на
две цели числа A/B, които нямат общ делител и представляват
несъкратима дроб. Значи поне едно от двете числа A и B
трябва да е нечетно. Сега да допуснем, че има такива числа и да
запишем
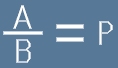 След като се уговорихме, че числото в дясно е корен от 2,
това значи че квадрата на двете страни от горното равенство
е точно 2.
След като се уговорихме, че числото в дясно е корен от 2,
това значи че квадрата на двете страни от горното равенство
е точно 2.
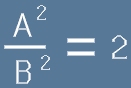 (1)
Числителя на дробта в ляво е двойно по-голям от знаменателя,
което значи, че е четно число. Но ако квадрата на A е четно
число, то и самото A е четно. Значи има цяло число Q, такова, че
(1)
Числителя на дробта в ляво е двойно по-голям от знаменателя,
което значи, че е четно число. Но ако квадрата на A е четно
число, то и самото A е четно. Значи има цяло число Q, такова, че
 Замествайки A с 2Q в по-горното равенство(1), виждаме, че
Замествайки A с 2Q в по-горното равенство(1), виждаме, че
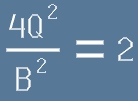 тоест
тоест
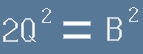 - квадрата на B е четно число.
Обаче ако квадрата на B е четно число, то и самото B е четно.
Оказа се, че и двете числа A и B са четни. Това противоречи на
допускането, че дробта A/B е несъкратима.
Заключението е, че такива цели числа A и B не съществуват.
- квадрата на B е четно число.
Обаче ако квадрата на B е четно число, то и самото B е четно.
Оказа се, че и двете числа A и B са четни. Това противоречи на
допускането, че дробта A/B е несъкратима.
Заключението е, че такива цели числа A и B не съществуват.
 - то е дължина на хипотенуза в правоъгълен триъгълник с катети 1.
Да означим числото корен квадратен от 2 с буквата P
и да допуснем, че P е рационално число.
Всяко рационално число може да се запише като отношение на
две цели числа A/B, които нямат общ делител и представляват
несъкратима дроб. Значи поне едно от двете числа A и B
трябва да е нечетно. Сега да допуснем, че има такива числа и да
запишем
- то е дължина на хипотенуза в правоъгълен триъгълник с катети 1.
Да означим числото корен квадратен от 2 с буквата P
и да допуснем, че P е рационално число.
Всяко рационално число може да се запише като отношение на
две цели числа A/B, които нямат общ делител и представляват
несъкратима дроб. Значи поне едно от двете числа A и B
трябва да е нечетно. Сега да допуснем, че има такива числа и да
запишем
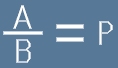 След като се уговорихме, че числото в дясно е корен от 2,
това значи че квадрата на двете страни от горното равенство
е точно 2.
След като се уговорихме, че числото в дясно е корен от 2,
това значи че квадрата на двете страни от горното равенство
е точно 2.
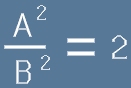 (1)
Числителя на дробта в ляво е двойно по-голям от знаменателя,
което значи, че е четно число. Но ако квадрата на A е четно
число, то и самото A е четно. Значи има цяло число Q, такова, че
(1)
Числителя на дробта в ляво е двойно по-голям от знаменателя,
което значи, че е четно число. Но ако квадрата на A е четно
число, то и самото A е четно. Значи има цяло число Q, такова, че
 Замествайки A с 2Q в по-горното равенство(1), виждаме, че
Замествайки A с 2Q в по-горното равенство(1), виждаме, че
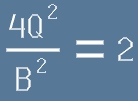 тоест
тоест
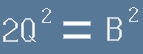 - квадрата на B е четно число.
Обаче ако квадрата на B е четно число, то и самото B е четно.
Оказа се, че и двете числа A и B са четни. Това противоречи на
допускането, че дробта A/B е несъкратима.
Заключението е, че такива цели числа A и B не съществуват.
- квадрата на B е четно число.
Обаче ако квадрата на B е четно число, то и самото B е четно.
Оказа се, че и двете числа A и B са четни. Това противоречи на
допускането, че дробта A/B е несъкратима.
Заключението е, че такива цели числа A и B не съществуват.