 Уравнение на Поасон
Уравнение на Поасон
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Трабва да сте чели:
Набла операциии,
статията за градиент от Станчо Павлов.
Изводът по-долу е от класическата физика. Свързан е с уравнението на Айнщайн за гравитационното поле, с електродинамиката и статистичестката физика.
Името на Поасон е написано на Айфеловата Кула. Уравненията по-долу са от публикация през 1813 г.
Градиент и Дивергенция
Набла операторът 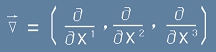 е вектор и може да бъде прилаган към скаларно поле -
както всеки вектор може да бъде умножен по число. Резултатът от такава операция е вектор и се нарича градиент.
е вектор и може да бъде прилаган към скаларно поле -
както всеки вектор може да бъде умножен по число. Резултатът от такава операция е вектор и се нарича градиент.
Ако умножим скаларно набла-вектора по векторно поле, получаваме скаларен резултат, наречен дивергенция.
Дивергенцията съкратено се означава с "div" и се определя като:
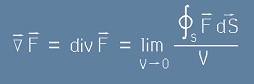 , [1]
, [1]
където интегрирането става по S - затворена повърхност, пронизвана от векторното поле F, а с буква V е означен
обхванатия вътре в тази повърхност обем.
Дивергенцията е скалар, определен с [1] за всяка точка от пространството.
Пак от [1] се разбира - интегрирайки двете му страни по обхванатия вътре обем V, че
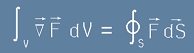 . [2]
. [2]
Равенството [2] понякога се нарича теорема за дивергенцията.
Дясната му страна е потока на полето F през затворена повърхност S,
а лявата - интеграл (тоест сбор) на дивергенцята в затворения вътре обем V.
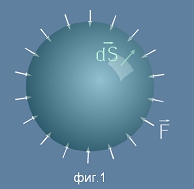
На фиг.1 е представена такава ситуация за гравитационно поле - ако допуснем, че около източник с маса M
е описана сфера, силовите вектори на полето F са насочени по радиуса навътре , а елементарният вектор на повърността
- надписан dS - е насочен навън.
Повърхността може да е с друга, различна от сфера форма, но винаги е спазено равенството
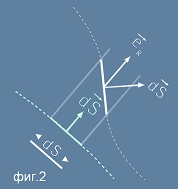
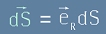 , [3]
, [3]
където в ляво е елементарният вектор на площта върху сфера, а в дясно - единичен вектор насочен по радиуса, умножен по скаларно представен
повърхностен елемент, тоест площта на проекцията на този елемент върху сферата (фиг.2).
Съгласно
Законът на Нютон за Гравитацията
полето, тоест силата действуваща на единична маса е
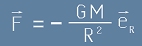 , [4]
, [4]
където М е масата на планетата, G е гравитационната константа, R2 - квадрат на разстоянието до центъра, eR - единичен вектор, насочен по радиуса.
Да опитаме повърхностния интеграл, записан в дясно на [2]. Съгласно [4] той ще изглежда така:
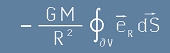 , [5]
, [5]
където с  е означен затворения обем.
Заместваме [3] в [5], Тогава [5] е еквивалентно на:
е означен затворения обем.
Заместваме [3] в [5], Тогава [5] е еквивалентно на:
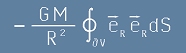 [6]. Очевидно под интеграла стои единица и това го прави колкото повърхност на сфера.
[6]. Очевидно под интеграла стои единица и това го прави колкото повърхност на сфера.
Да заместим обратно полученото в [2]:
 . [7]
. [7]
Няма начин да не се сетим, че ако под интеграла в ляво стоеше плътност, отдясно трябваше да стои маса:
 . [8]
. [8]
Съпоставяйки последните две равенства [8] и [7] с [2], стигаме до
важно уравнение - ще го наречем временно Уравнение на Поасон. Това уравнение е явно използувано в други статии:
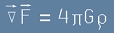 . [9]
. [9]
Но всъщност постановката на Поасон заслужава малко повече внимание.
Нека f(x,y,z) и s(x,y,z) са две скаларни функции в тримерно пространство. Изобщо казано,
Уравнението на Поасон
е диференциално уравнение, в което от известна функция s се търси друга функция f.
 То има следния вид:
То има следния вид:
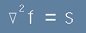 . [10]
. [10]
Търсената функция f се нарича Потенциал (Поасонов потенциал). Известната функцията s се нарича източник.
Тъй като f и s са дефинирани върху едно и също аргументно множество, източника на полето
трябва да е зададен като функция s(x,y,z) върху цялото пространство. Ако източника е еднородно тяло с ясни граници,
то функцията s(x) изглежда както е на фиг.3.
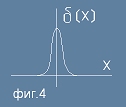 За точкови заряди и материални точки се използува специално построена функция,
наречена Делта-Функция на Дирак, чийто вид е показан като идея на фиг.4.
Делта-Функцията на Дирак по дефиниция е нула за всяко ненулево x, има безкрайна стойност
в точката нула и е нормирана чрез условието
За точкови заряди и материални точки се използува специално построена функция,
наречена Делта-Функция на Дирак, чийто вид е показан като идея на фиг.4.
Делта-Функцията на Дирак по дефиниция е нула за всяко ненулево x, има безкрайна стойност
в точката нула и е нормирана чрез условието
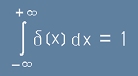 . [11]
. [11]
По същество това е спектър (разпределение), затова
размерността на Делта-функцията на Дирак е 1/x, каквото и да е x - тоест горният интеграл е числова единица.
Ако x и x' са независими реални аргументи - променливи от едно и също множество, то Делта-Функцията на Дирак позволява следната операция:
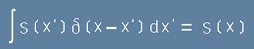 . [11.1]
. [11.1]
която може да се нарече "смяна на аргумента" - и е полезна в някои случаи.
В тези равенство [11], [11.1] и в следващите по-долу, ползувам едномерно x,
вместо означение за 3D координатна точка - за опростен запис.
Суперпозиция
Нека си представим, че f е решение на [10]. Ако умножим функцията s от дясната страна на [10] по константа, произведението на същата константа по f ще е решение на новото уравнение.
Ако в дясно стои линейна комбинация от s - функции, решението ще е същата линейна комбинация от решения за всяко s.
Да допуснем, че в точка x' има заряд и че този заряд създава потенциал G(x,x').
Това значи, да допуснем, че функцията G(x,x') е решение на [10] за единичен точков заряд:
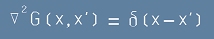 . [13]
. [13]
(Тази функция - G - се нарича Функция на Грийн. Обратно на Делта-функцията, G има размерността на x)
В такъв случай сбора (интеграла)
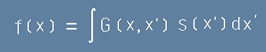 [14]
[14]
е линейна комбинация от решения на [10], разпределена както функцията s.
Да проверим дали [14] удовлетворява [10]. Първо да забележим, че:
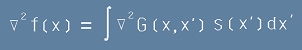 [15]
[15]
и да заместим [13] в [15]:
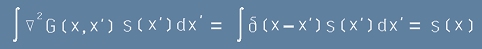 . [16]
. [16]
Като погледнем последните две равенства [15] и [16], виждаме, че
действително [14] е решение на Поасоновото уравнение.
Описаното производство на решения чрез функция на Грийн не зависи от вида на функцията-източник s.
Означенията "x" в равенствата по-горе би трябвало да се тълкуват като вектори - координатни тройки,
за да са смислени набла операциите.
От уравнението [10] следва, че функцията f трябва да спазва размерност [s]/[x]2.
коментари
Радостин Желязков 18.03.2011
________________________________________________________________________________________
учебни статии по физика
 Уравнение на Поасон
Уравнение на Поасон
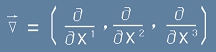 е вектор и може да бъде прилаган към скаларно поле -
както всеки вектор може да бъде умножен по число. Резултатът от такава операция е вектор и се нарича градиент.
е вектор и може да бъде прилаган към скаларно поле -
както всеки вектор може да бъде умножен по число. Резултатът от такава операция е вектор и се нарича градиент.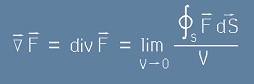 , [1]
, [1]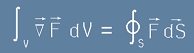 . [2]
. [2]

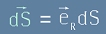 , [3]
, [3]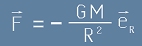 , [4]
, [4]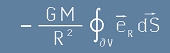 , [5]
, [5] е означен затворения обем.
Заместваме [3] в [5], Тогава [5] е еквивалентно на:
е означен затворения обем.
Заместваме [3] в [5], Тогава [5] е еквивалентно на: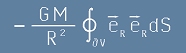 [6]. Очевидно под интеграла стои единица и това го прави колкото повърхност на сфера.
[6]. Очевидно под интеграла стои единица и това го прави колкото повърхност на сфера.  . [7]
. [7] . [8]
. [8]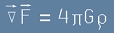 . [9]
. [9] То има следния вид:
То има следния вид: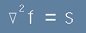 . [10]
. [10] За точкови заряди и материални точки се използува специално построена функция,
наречена Делта-Функция на Дирак, чийто вид е показан като идея на фиг.4.
Делта-Функцията на Дирак по дефиниция е нула за всяко ненулево x, има безкрайна стойност
в точката нула и е нормирана чрез условието
За точкови заряди и материални точки се използува специално построена функция,
наречена Делта-Функция на Дирак, чийто вид е показан като идея на фиг.4.
Делта-Функцията на Дирак по дефиниция е нула за всяко ненулево x, има безкрайна стойност
в точката нула и е нормирана чрез условието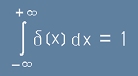 . [11]
. [11]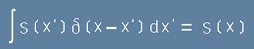 . [11.1]
. [11.1]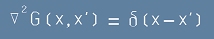 . [13]
. [13]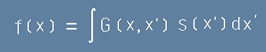 [14]
[14]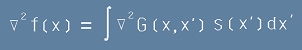 [15]
[15]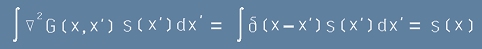 . [16]
. [16]