 Набла операции
Набла операции
Помощна статия
Трябва да сте запознати с:
Векторно произведение ,
Частни производни.
Погледнете и Статията за градиент.
В този текст са ползувани долни и горни индекси, но при декартови координати,
както е в класическата физика, това няма значение.

Набла оператор
Да изберем пространство с координатни индекси 1,2,3.
По дефиниция Набла операторът е вектор с компоненти:
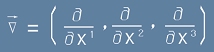 , или кратко
, или кратко
 . [1]
. [1]
Резултатът от прилагането му е равносилен на бинарна операция, в която първият операнд е вектор, а вторият
може да е скаларна, или векторна функция върху същото пространство.
Набла операторът се нарича още Оператор на Хамилтон.
Думата "Набла" е название за старинен струнен музикален инструмент (фиг.1).
Градиент
Ако f е скаларна функция на трите координати f (x1,x2,x3) ,
то резултатът от Набла-операцията с вектора f се нарича Градиент - grad f.
Това е еквивалентна операция на умножение вектор по число.
Означава с "grad" и представлява вектор с координати
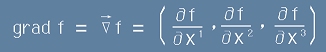 , или кратко
, или кратко
 . [2]
. [2]
Дивергенция
Ако f е векторна функция на трите координати f (x1,x2,x3) ,
то резултатът от скаларното умножение на вектора Набла по вектора f се нарича Дивергенция.
Дивергенцията е скалар (число) и е комутативна операция. Означава се с "div" и представлява сбор:
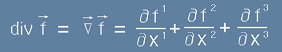 , или кратко
, или кратко
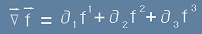 . [3]
. [3]
Една различна дефиниция, водеща веднага до Теоремата за Дивергенцията е показана в статията "Уравнение на Поасон".
Ротация
Ако f е векторна функция на трите координати f (x1,x2,x3) ,
то резултатът от векторното умножение на вектора Набла по вектора f се нарича Ротация.
Еквивалент на векторно произведение на два вектора.
Не е комутативно. Означава се с "rot" и представлява вектор с координати
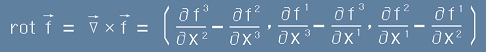 , или кратко
, или кратко
 . [4]
. [4]
Понякога е удобно представянето
 . [4.1]
. [4.1]
Друга дефиниция, водеща веднага до Теоремата за Ротацията е показана в статията "Уравнения на Максуел".
Набла е производна
Правилото на Лайбниц е приложимо. Според Спас Манолов и др. Държавно издателство Техника 1977 г. стр 124
"Ако операторът набла действа на произведение от две полета, то той е равен на сумата от две събираеми, като
в първото събираемо набла действа на единия множител, а на другия не действа а във второто събираемо имаме обратното".
С наши означения това изглежда така:
Ако u v са скаларни полета, то  ; [L1]
; [L1]
Ако u е скаларно, а F е векторно поле, то 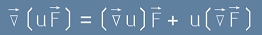 . [L2]
. [L2]
Aко A и B са две векторни полета
и ако A е скаларно умножено по B, то 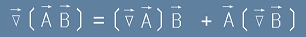 . [L3]
. [L3]
* * *
В страниците са използувани някои важни моменти от набла-смятането:
Тъждествo 1
div rot f = 0.
Коментар: Ротацията е векторно произведение и резултатът е вектор, перпендикулярен на двата операнда, в частност на вектора Набла.
В този случай дивергенцията - като скаларно произведние между два перпендикуларни вектора е винаги нула.
Тъждествo 2
 . [5]
. [5]
Доказателство: Да означим лявата част с L и да я пресметнем:
 . [6]
. [6]
Да означим двете съставки от дясната страна на [5] с R1 и R2:
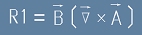 ,
,
 .
.
Сега да разкрием скобите за L:
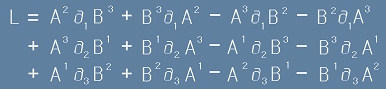 [7]
[7]
И после за R1 и R2:
 , [8]
, [8]
 [9]
[9]
От [7] , [8] , [9] се вижда, че L = R1 - R2, с което [5] е доказано.
Коментар:
Тройката "набла ( A x B )" може да се разглежда като
смесено произведение.
коментари
Радостин Желязков 31.03.2011
с любезното съдействие на Станчо Павлов
________________________________________________________________________________________
учебни статии по физика
 Набла операции
Набла операции
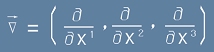 , или кратко
, или кратко
 . [1]
. [1]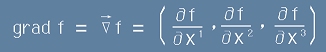 , или кратко
, или кратко
 . [2]
. [2]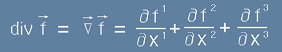 , или кратко
, или кратко
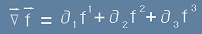 . [3]
. [3]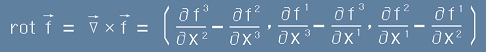 , или кратко
, или кратко
 . [4]
. [4] . [4.1]
. [4.1] ; [L1]
; [L1]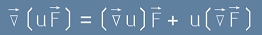 . [L2]
. [L2]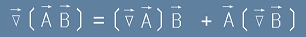 . [L3]
. [L3] . [5]
. [5] . [6]
. [6]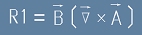 ,
,
 .
.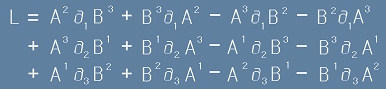 [7]
[7] , [8]
, [8] [9]
[9]