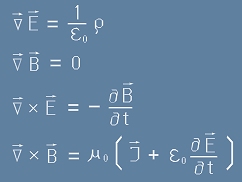Уравнения на Максуел
Уравнения на Максуел
Огромна част от съвременните знания са постигнати през 19 век - класическия период. Ето малка поредица за имената и законите:
1793 Закон на Кулон;
1813 Уравнение на Поасон;
1820 Закон на Био-Савар;
1826 Закон на Ампер;
1827 Закон на Ом;
1831 Закон на Фарадей за електромагнитната индукция;
1835 Закон на Гаус за магнитното поле;
1862 Уравненията на Максуел;
1888 Херц открива електромагнитните вълни;
1892 Лоренцовата сила върху движещ се електричен заряд.
Трябва да сте запознати с:
Набла операции,
Формула на Грин,
Уравнение на Поасон.
Електрично поле
В статията "Уравнение на Поасон" беше показана ясна връзка между гравитационното поле според закона на Нютон
и източника на гравитацията - масовата плътност.
Законът на Кулон за електростатичната сила има същата форма
q1q2/r2,
както Нютоновото привличане
m1m2/r2.
Електричното поле (сила действуваща на единица заряд), се изразява като
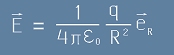 , [1]
, [1]
където епислон е константа, R2 е квадрата на разстоянието до заряда q - източник на полето,
eR - единичен вектор насочен по радиуса.
Тази формула води до аналогично уравнение за дивергенцията на електричното поле,
каквото е [9] от статията Поасон.
Ще повторим стъпка по стъпка пътя до това уравнение спрямо вектора E.
Да разгледаме затворена повърхност S, вътре в която обемът е V, така, че заряда q е вътре в този обем.
Теоремата за дивергенцията спрямо векторното поле E изглежда така:
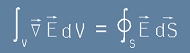 , [1.1]
, [1.1]
Нормалният вектор dS към повърхността може да се изрази с единичен радиус вектор,
умножен по числовата проекцията на dS върху сфера (виж [3] от статията Уравнение на Поасон как точно става това):
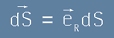 . [1.2]
. [1.2]
Заместваме [1.2] и [1] в [1.1]. Получаваме
 . [1.3]
. [1.3]
Последният интеграл е всъщност повърхност на сфера и от [1.3] остава
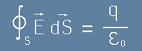 . [1.4]
. [1.4]
Зарядът q от дясната страна на [1.4] може да се изрази чрез интеграл плътност по обем:
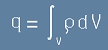 . [1.5]
. [1.5]
Да заместим това в [1.4] и с полученото да заменим дясната страна на [1.1]. Ще получим
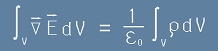 . [1.6]
. [1.6]
След като тези два интеграла са равни, подинтегралните им функции също са равни. Така получаваме уравнение - известно още като
Първо уравнение на Максуел.
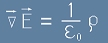 , [1m]
, [1m]
където с ро е означена плътността на заряда, а с малка гръцка буква епсилон в знаменателя е означена
известната природна константа - диелектричната проницаемост на вакуума.
Това уравнение е известно и като Закон на Гаус за електричното поле.
* * *
Сега да разгледаме магнитните сили. Нека да отговорим на следния въпрос:
Възможно ли е формула подобна на закона на Нютон за гравитацията, или закона на Кулон за електростатичното привличане
да описва и магнитната сила?
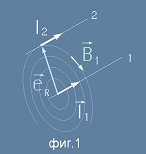
Отговорът е "Да". Трябва само малко анализ. Да си представим два участъка с единична дължина от успоредни проводници,
и да допуснем, че по тези участъци текат два тока I1 и I2,
а свързващата ги права е перпендикулярна на техните направления. (фиг.1)
Да означим с R2 квадрата на разстоянието между тях.
В такъв случай, за големината на магнитната сила действително важи формула от вида:
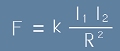 , където k е някакъв коефициент.
, където k е някакъв коефициент.
Щом проводниците са успоредни, те лежат в една равнина. Да означим с eR единичния вектор от I1 до I2.
Първият ток създава магнитно поле,
чиито силови линии са концентрични окръжности в равнина, перпендикулярна на направлението му.
Векторът на силата е перпендикулярен на свързващата права и допирателен към една от
магнитните силови окръжности. Магнитното поле
(сила, действуваща на един ампер от тока I2)
се означава с B и би изглеждала аналогично на [1], но пространствените посоки на трите вектора в този случай
съответствуват на векторно произведение (закон на Био-Савар-Лаплас):
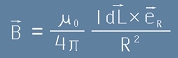 . [5]
. [5]
Тази формула [5] показва поле, създавано от проводник с дължина dL на разстояние R,
в посока по единичен вектор eR. Малката гръцка буква мю е природна константа - магнитната проницаемост на вакуума.
Съгласно фиг.1, полето действуващо върху тока I2 би трябвало да е
суперпозиция (тоест интеграл) на [5] по цялата дължина на проводника 1.
В статията "Уравнение на Поасон" е казано какво е градиент (мат. grad) и какво е дивергенция (мат. div).
Да обърнем внимание, че тези две векторни операции са комутативни. Първото уравнение на Максуел [1m] казва
каква е дивергенцията на електричното поле.
Дивергенцията е всъщност скаларно умножение.
Ако двата операнда-вектори са взаимно перпендикулярни, дивергенцията е нула.
Но точно това би се получило, ако приложим набла-операция върху магнитното поле от [5],
защото набла-векторът е насочен по eR.
 . [2m]
. [2m]
Това равенство [2m] се нарича
Второ уравнение на Максуел
Казано с думи - магнитното поле има нулева дивергенция - няма източник, какъвто е заряда за електричното поле.
Същото [2m] е споменавано и под името Закон на Гаус за магнитното поле.
* * *
Максуел е живял по време, когато електричеството е било на първа линия в науката. За него са били известни много неща. Едно от тях е
Електромагнитната индукция
Това явление е изследвано от Майкъл Фарадей - ако в променливо магнитно поле има затворен проводник (линеен контур),
в него възниква ток - пропорционален на скоростта с която се променя магнитния поток обхванат от контура.
Според закона на Ом, токът е пропорционален на напрежението, което от своя страна е линеен интеграл на електричното поле по контура L.
Промяната в потока на магнитното поле Ф за единица време означава производна:
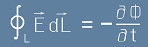 [6].
[6].
Знакът минус в дясната страна на [6] изразява правилото на Ленц, че
индуцираният ток има посока, обратна на посоката на тока, създаващ магнитното поле.
* * *
Набла операторът може да бъде векторно умножен (некомутативно!) по векторно поле и резултатът от това умножение е
нов вектор, наречен
Ротация
Математическото означение на тази операция е "rot":

Английската дума за ротация е curl (вихър, завихряне). Означението "rot" се ползува в
Германия, Франция, Русия, Испания, Италия, също и в български публикации.
Резултатът от векторното умножение е вектор перпендикулярен на двата операнда.
За разбирането на тази дума е полезна Формулата на Грин и сведенията в статията "Набла операции" /има линкове по-горе, в началото/.
 В съвременната литература се среща следната
В съвременната литература се среща следната
Дефиниция:
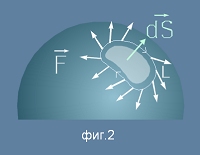
Нека dS е нормалния вектор към някакъв участък от повърхност с големина S, обграден от контур L (виж фиг.2);
Нека векторното поле F е дефинирано във всяка точка от тази повърхност. Тогава ротацията на
полето F - през повърхността S се дефинира като вектор - rot F - такъв, че:
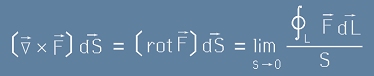 [7] ,
[7] ,
където интегрирането е по затворения контур L, а S е големината на площта обхваната от контура.
Повърхността трябва да ориентирана и непрекъсната.
Ако интегрираме двете страни на [7] по повърхността вътре в контура, ще получим равенството
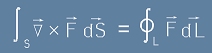 [8] ,
[8] ,
известно още като теорема за ротацията.
Дясната страна на [8] досущ прилича на лявата страна от [6]. Магнитният поток, споменат в дясно на [6]
представлява интеграл на магнитното поле B пронизващо повърхността S затворена в контура:
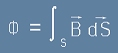 ,
следователно
,
следователно
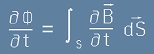 [10] ,
[10] ,
а подреждането на [8], [10] и [6] казва, че
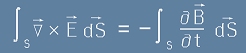 [11] .
[11] .
Както виждаме, подинтегралните функции в двете страни на [11] трябва да са равни. Стигаме до
Третото уравнение на Максуел
което изглежда така:
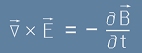 [3m] .
[3m] .
* * *
Друго известно уравнение от онова време е
Законът на Ампер
Около всеки ток (по проводник) възниква магнитно поле, чиито силови линии са концентрични окръжности
в равнина перпендикулярна на проводника. Ако проводника е дълъг и прав, а токът е постоянен, магнитното
поле B е пропорционално на тока I и обратно пропорционално на разстоянието R до проводника.
 Формулата (за големини и при неуточнен коефициент k) е проста:
Формулата (за големини и при неуточнен коефициент k) е проста:
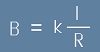 .
Скоро е било установено, че
.
Скоро е било установено, че 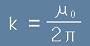 , така, че истинският вид на тази
формула е
, така, че истинският вид на тази
формула е
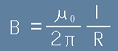 [12].
[12].
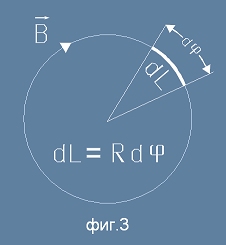
 Магнитните силови линии са окръжности. Да разгледаме една от тях (фиг.3)
и да пресметнем интеграла на вектора B по окръжността, имайки предвид [12] :
Магнитните силови линии са окръжности. Да разгледаме една от тях (фиг.3)
и да пресметнем интеграла на вектора B по окръжността, имайки предвид [12] :
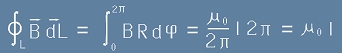 [13] ,
[13] ,
където I е тока по проводника.
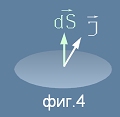
Като явление електричният ток е движение на заряди и ако усредним скоростта v
на движещите се заряди с плътност ро -
се образува вектор - плътност на тока:
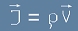 (фиг.4).
Макар, че точно в нашия случай векторите J и dS лежат на една права, ще се възползуваме от тази картинка,
защото след малко това ще ни трябва по същество.
(фиг.4).
Макар, че точно в нашия случай векторите J и dS лежат на една права, ще се възползуваме от тази картинка,
защото след малко това ще ни трябва по същество.
Ако представим тока I като интеграл
(плътност J на тока) х (площта S обградена от силовата линия) :
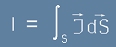 [14], ще получим
[14], ще получим
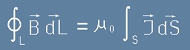 [15].
[15].
Да напишем за вектора B теоремата за ротацията от по-горе [8]:
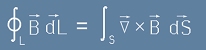 [16],
[16],
Съпоставката на [15] и [16] води до едно важно равенството, наричано
закон на Ампер за циркулацията на магнитното поле:
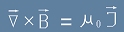 [17].
[17].
Почти стигнахме до последното уравнение. В началото самият Максуел е гледал на [17] като на последно от системата.
Но в това уравнение има ограничение. Нека да пресметнем дивергенцията на двете му страни:
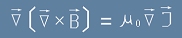 [18].
Лявата страна на това уравнение е нула, защото набла векторът е скаларно умножен по перпендикулярен на него вектор.
Излиза, че и дясната страна трябва да е нулева:
[18].
Лявата страна на това уравнение е нула, защото набла векторът е скаларно умножен по перпендикулярен на него вектор.
Излиза, че и дясната страна трябва да е нулева:
 [19].
[19].
Това не е много чудно, след като постановката на Ампер предполага постоянен ток.
За повече общност, да разгледаме обем V вътре в затворена повърхност S.
Зарядът q в този обем е обемен интеграл от плътността ро - като функция от координатите:
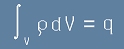 . [20]
. [20]
Да допуснем, че през повърхността преминава още заряд - така, че затвореният в обема V заряд q се променя.
Промяната dq/dt очевидно е поток на заряда през цялата повърхност S.
Ако J е вектора на плътността на тока (фиг.4 - ампери на квадратен метър) през повърхността S,
- дори да не е по нормалата! - то промяната в заряда ще е толкова, колкото е интеграла на J през S :
 , [21]
, [21]
или, имайки предвид [20], получаваме равенство, изразяващо факта, че изобщо
Електричният заряд се запазва
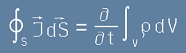 , [22]
, [22]
Да си спомним и напишем
теоремата за дивергенцията за вектора J:
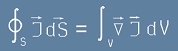 , [23]
, [23]
Левите страни на [23] и [22] са равни, както и условията за интегриране от дясно.
Следователно
 , [24]
, [24]
където вече виждаме ясен конфликт с [19] .
(Променлива плътност на заряда се наблюдава например в електрическия кондензатор.)
Плътността на заряда е показана като източник на електрично поле в [1m].
Производната на двете му страни по времето дава:
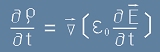 , [25]
, [25]
но изразът в скобите има същата размерност, каквато има плътност на тока - точно каквото е J от [24] - това е ток.
Максуел е нарекъл тока от скобите на [25] с името
Ток на Отместване
за разлика от обикновения ток, който оттогава се преименува в "ток на проводимост".
Нещо повече. Максуел допуска, че тока на отместване възниква винаги и навсякъде - дори във вакуум и неотменно трябва да бъде добавен
в дясната страна на [17] - и така
Четвъртото уравнение на Максуел
има следния вид:
 . [4m]
. [4m]
Всички заедно
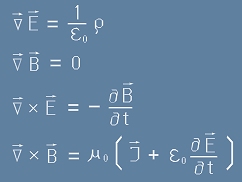
коментари
Радостин Желязков 26.03.2011 / кор. 30.05.2011
________________________________________________________________________________________
учебни статии по физика
 Уравнения на Максуел
Уравнения на Максуел
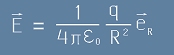 , [1]
, [1]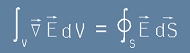 , [1.1]
, [1.1]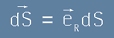 . [1.2]
. [1.2] . [1.3]
. [1.3]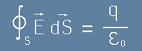 . [1.4]
. [1.4]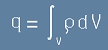 . [1.5]
. [1.5]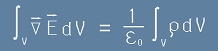 . [1.6]
. [1.6]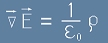 , [1m]
, [1m]
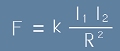 , където k е някакъв коефициент.
, където k е някакъв коефициент.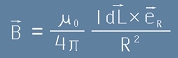 . [5]
. [5] . [2m]
. [2m]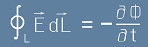 [6].
[6].
 В съвременната литература се среща следната
В съвременната литература се среща следната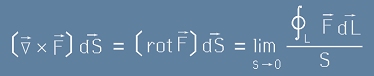 [7] ,
[7] ,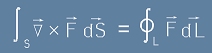 [8] ,
[8] ,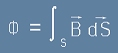 ,
следователно
,
следователно
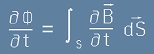 [10] ,
[10] ,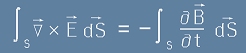 [11] .
[11] . 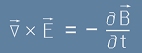 [3m] .
[3m] .  Формулата (за големини и при неуточнен коефициент k) е проста:
Формулата (за големини и при неуточнен коефициент k) е проста: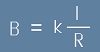 .
Скоро е било установено, че
.
Скоро е било установено, че 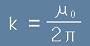 , така, че истинският вид на тази
формула е
, така, че истинският вид на тази
формула е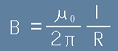 [12].
[12]. Магнитните силови линии са окръжности. Да разгледаме една от тях (фиг.3)
и да пресметнем интеграла на вектора B по окръжността, имайки предвид [12] :
Магнитните силови линии са окръжности. Да разгледаме една от тях (фиг.3)
и да пресметнем интеграла на вектора B по окръжността, имайки предвид [12] :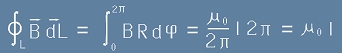 [13] ,
[13] ,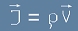 (фиг.4).
Макар, че точно в нашия случай векторите J и dS лежат на една права, ще се възползуваме от тази картинка,
защото след малко това ще ни трябва по същество.
(фиг.4).
Макар, че точно в нашия случай векторите J и dS лежат на една права, ще се възползуваме от тази картинка,
защото след малко това ще ни трябва по същество.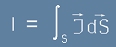 [14], ще получим
[14], ще получим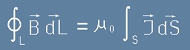 [15].
[15].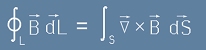 [16],
[16],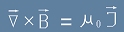 [17].
[17].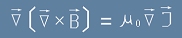 [18].
Лявата страна на това уравнение е нула, защото набла векторът е скаларно умножен по перпендикулярен на него вектор.
Излиза, че и дясната страна трябва да е нулева:
[18].
Лявата страна на това уравнение е нула, защото набла векторът е скаларно умножен по перпендикулярен на него вектор.
Излиза, че и дясната страна трябва да е нулева: [19].
[19].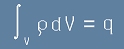 . [20]
. [20] , [21]
, [21]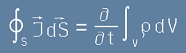 , [22]
, [22]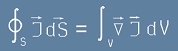 , [23]
, [23] , [24]
, [24]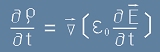 , [25]
, [25] . [4m]
. [4m]