 Напрежение
Напрежение
По-рано в тази поредица тензорите са коментирани в статията Матрицата III.
В този материал обаче става дума за понятието "тензор" (англ. tension-напрежение), свързано с класическата механика.
Всичко по-долу е в декартова координатна система.
Предговор
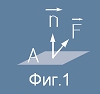 Напрежението се дефинира като сила действуваща на единица повърхност.
Напрежението се дефинира като сила действуваща на единица повърхност.
Да си представим, че някаква равнина разделя едно тяло на две.
Нека някъде по тази равнина - вътре в тялото е определена площадка A с нормален вектор n (виж Фиг.1)
и в центъра на тази площадка е приложена сила F.
Изразът "Сила действуваща на единица повърхност"
може да се сведе до формулата за налягане P=F/A - това ще важи само ако двете F A се разглеждат като числа (скалари),
при което силата F трябва да действува перпендикулярно на площта А.
Но в общия случай, както се вижда от дефиницията по-долу, в края на този текст, напрежението представлява три тройки числа - тензор.
Да определим вектора T като производна на F спрямо големината на площадката A:
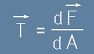 . [1]
. [1]
Английското наименование за този вектор е "Traction Vector". Аз не можах да преведа това на български език и за да избегна
чуждицата "тракция", ще използувам "Сила върху Единична Повърхност" - СЕП. Да забележим, че в [1] T и dF са вектори, докато dA е скалар.
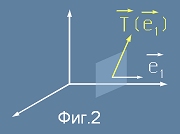
Нека тройката вектори e1,e2,e3 образува декартов базис. Да изберем площадка с единична повърхност, чийто нормален вектор съвпада с e1.
Да означим с T(e1) СЕП вектора спрямо тази e1-площадка (виж Фиг.2).
Ако направим същото и спрямо другите два координатни вектора, ще получим три СЕП-вектора:
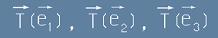 - с компоненти ( j = 1,2,3 )
- с компоненти ( j = 1,2,3 )
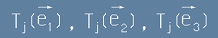 . [2]
. [2]
 (На други места координатните вектори се означават със шапка - символ "^" , но тук ние ги тълкуваме
като нормални вектори към повърхност, затова означението остава стрелка над буква.)
(На други места координатните вектори се означават със шапка - символ "^" , но тук ние ги тълкуваме
като нормални вектори към повърхност, затова означението остава стрелка над буква.)
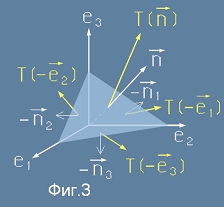
Да разгледаме тетраедъра на Фиг.3 - малък обем с избрана удобна форма.
По стената съвпадаща с координатна равнина e1 e2 действува
СЕП-вектор означен с T(-e3). Аналогично за другите два T(-e1) и T(-e2).
Съгласно [1], действителната сила върху площадката dA е
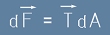 . [3]
. [3]
Същото важи и за останалите три стени на тетраедъра:
 , [4]
, [4]
 , [5]
, [5]
 . [6]
. [6]
Да заместим сбора от всички сили [3] .. [6] във формулата на Нютон F=ma:
 . [7]
. [7]
/по-долу, към края на този текст, има коментар за пълната сила/
и да разделим [7] на dA:
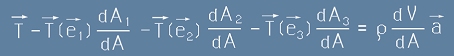 . [8]
. [8]
От формата на тетраедъра следва, че трите координатни стени са проекции на dA. Значи
 ;
;
 ;
;
 . [9]
. [9]
Вземайки предвид, че обема намалява по-бързо от повърхността, тоест
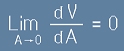 , [9.1]
, [9.1]
от [8] и [9] остава
 ,
,
a j-компонентата на СЕП вектора спрямо площадка с нормален вектор n ще бъде
 . [10]
. [10]
Тензор на напрежението
Нека e1, e2, e3 съставят декартов базис. Нека T(e1), T(e2), T(e3) са вектори на СЕП (Сила действуваща на Единична
Повърхност) по елементарни площадки, чиито нормали са e1 e2 e3.
Елементите на Тензорът на Коши за Напрежението се дефинират като
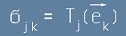 , или подробно
, или подробно
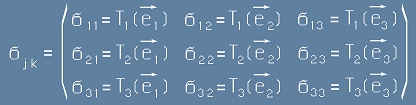 . [11]
. [11]
Ако е известно тензорното поле на напрежението, за коя да е повърхност с нормален вектор n,
векторите на Силата към Единица Повърхност се смятат по формулата (сума по повтарящи се индекси) :
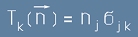 . [12]
. [12]
която е пряко следствие от [10] и дефиницията [11].
Последното твърдение [12] понякога се нарича
Теорема на Коши
за Тензора на Напрежението.
Освен силите действуващи по повърхността на тялото, сумирани в равенството на Нютон от по-горе [7],
е добре да уточним, че е възможна и сила, която произхожда от самата среда (масата) на тялото - например гравитация. Такава сила
не би променила изведеното в [10], тъй като съображенето за малки обеми [9.1] ще елиминира нейното действие.
Но в някои следващи места може да има препратка към
Пълната сила
действуваща на елемент от тялото.
Тя има вид (вместо [7] от по-горе):
 , [13]
, [13]
където b е означение за вектора на силата действуваща в единица обем вътре в тялото.
Радостин Желязков 09.02.2012 /последна редакция 19.02.2012/
________________________________________________________________________________________
коментари
учебни статии по физика
 Напрежение
Напрежение
 Напрежението се дефинира като сила действуваща на единица повърхност.
Напрежението се дефинира като сила действуваща на единица повърхност.
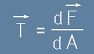 . [1]
. [1]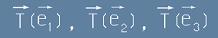 - с компоненти ( j = 1,2,3 )
- с компоненти ( j = 1,2,3 )
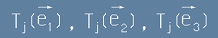 . [2]
. [2] (На други места координатните вектори се означават със шапка - символ "^" , но тук ние ги тълкуваме
като нормални вектори към повърхност, затова означението остава стрелка над буква.)
(На други места координатните вектори се означават със шапка - символ "^" , но тук ние ги тълкуваме
като нормални вектори към повърхност, затова означението остава стрелка над буква.)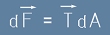 . [3]
. [3] , [4]
, [4] , [5]
, [5] . [6]
. [6] . [7]
. [7]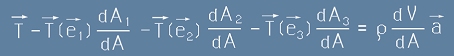 . [8]
. [8] ;
;
 ;
;
 . [9]
. [9]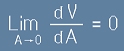 , [9.1]
, [9.1] ,
, . [10]
. [10]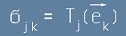 , или подробно
, или подробно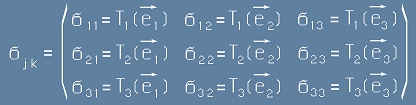 . [11]
. [11]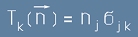 . [12]
. [12] , [13]
, [13]