 Матрицата III - революция
Матрицата III - революция
Този текст подпомага разбирането на математическия апарат в
Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I и Матрицата II.
Вижте какво пише в сайта на Станчо Павлов
за множествата.
Малко за тензорите
Имаме няколко именувани: Метричен тензор, Тензор на Минковски... и ще има още.
Всички те принадлежат към общност, чиито главни особености е добре да знаем.
Основната идея на тензорите е да представят геометрични или физични обекти по начин независещ от отправната координатна система.
Изобщо те изглеждат като матрици с 2,3 или повече размерности.
Съставени са от два типа компоненти: векторни и дуално-векторни (тоест контравариантни и ковариантни).
Тензор е обобщение от понятието за вектор, затова можем да приемем следното индуктивно правило:
1. Контравариантния вектор е тензор от тип (1,0) - горен индекс:
Tk;
2. Ковариантния вектор е тензор от тип (0,1); - долен индекс:
Tk;
3. Ако умножим декартово тензор от тип (k,r) по тензор от тип (1,0), получаваме тензор от тип (k+1,r), тоест ако m=k+1:
Ti1,i2,..imj1,j2,..jr;
4. Ако умножим декартово тензор от тип (k,r) по тензор от тип (0,1), получаваме тензор от тип (k,r+1), тоест ако n=r+1:
Ti1,i2,..ikj1,j2,..jn;
Определящо свойство на тензорите е, че при преход от една координатна система в друга се преобразуват по формулата:
Тi'k' = аi'n аk'p Тnp,
където a е матрица на прехода.
Забележете, че примовете се слагат към индекса i, а не към буквата T - за да се знае, че
не физическият обект T се променя, а само i-тата му компонента в примова координатна система.
Елементите на преобразуващите матрици са означени с
аi'k
и най-често работят в посока отдясно наляво.
Тези елементи имат характер 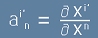 , тоест координатни преобразувания.
По един такъв преобразуващ елемент се полага на всеки индекс от тензора, съобразно типа му.
, тоест координатни преобразувания.
По един такъв преобразуващ елемент се полага на всеки индекс от тензора, съобразно типа му.
Тензорите могат да се събират, умножават по число и чрез тензорно (некомутативно) умножение.
Тензорното произведение AB=C се записва като:
 .
Например метричният тензор може да се изрази като
.
Например метричният тензор може да се изрази като
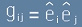 , а дуалният е
, а дуалният е 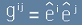 .
.
При тензорните равенства всяко събираемо в лявата и дясната страна трябва да има еднакви по тип и име неповтарящи се свободни индекси.
Допустимо е в някои член да има двойка повтарящи се индекси и това се тълкува като сбор (правило на Айнщайн за контракция).
В такъв случай единият индекс трябва да е ко, а другия - контравариантен.
Тензорите могат да бъдат чисто контравариантни
Tij
или чисто ковариантни
Tij
или смесени
Tij ;
Tij.
Тензорът е симетричен по два индекса i,j - когато
Tij = Tji
и е антисиметричен по i,j - когато
Tij = -Tji.
Поредността на индексите върви отляво надясно и не бива да се бърка с типа им.
Размяната на поредността на два индекса е еквивалент на плоско транспониране спрямо тези два индекса.
Ако тензорът е симетричен спрямо тези два индекса, той не се променя при транспониране.
Понякога е удобно да гледаме на един индекс от тензора като на вектор от съответния тип.
Например един индекс може "да се качи" или "да слезе" - както беше показано в статията
Матрицата I чрез ковариантен метричен тензор
Vi = gik Vk, или чрез контравариантен метричен тензор
Vi = gik Vk.
 Трансформации
Трансформации
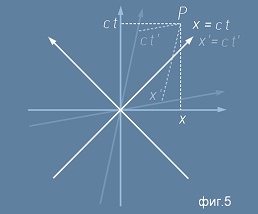
Ако едно събитие (пространствено-временна точка P) има координати ct и x,
в друга координатна система същата точка ще има координати ct' и x', получени чрез
Лоренцовите преобразувания.
В пространствено временна диаграма това е показано на фиг.5.
В примовата координатна система линията x'=ct' съвпада с x=ct, за да е спазен
постулата за една и съща стойност на скоростта на светлината. От същата фигура се вижда,
че координатните оси ct' и x' образуват афинна координатна система /остроъгълен базис/.
Интервалът на Минковски в случая съответствува на дистанцията от началото
на координатната система до точката P - той не варира при трансформацията.
Трансформациите представляват "оглеждане" на предметите. Когато разглеждаме нещо непознато,
обикаляме около него, за да видим как изглежда то от различни гледни точки. Ако можем,
го вземаме в ръце и го въртим - със същата цел. Това съответствува на трансформация - смяна на
отправната координатна система. Дефинициите на скалари, вектори и тензори носят такъв характер -
един обект се определя от начина, по който се променя образа му при трансформиране.
Вектор и базис
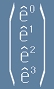
Нека  , или схематично
, или схематично  са базисни единични вектори в пространството на Минковски.
са базисни единични вектори в пространството на Минковски.
Какъв да е вектор V се представя чрез базисните вектори като
 , или по-кратко
, или по-кратко
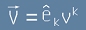 [6].
[6].
В друг базис - същият вектор V ще има други компоненти,
които се получават с Лоренцова трансформация (матрица 4х4) от V към V', по формула
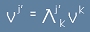 , или по-нагледно
, или по-нагледно
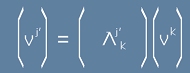 [6.1].
[6.1].
Нека означим с примове компонентите на другия базис:  ,
или схематично
,
или схематично  .
.
В този (примов) базис същият вектор може да се представи като линейна комбинация на базисните вектори
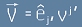 , или пък матрично
, или пък матрично
 и ако заместим от [6.1], получаваме
и ако заместим от [6.1], получаваме
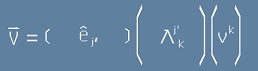 , тоест
, тоест
 [7].
[7].
Ако съпоставим [7] и [6], виждаме връзка между двата комплекта базисни вектори :
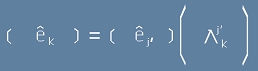 .
Да умножим отдясно с инверсната матрица (по уговорка означена с):
.
Да умножим отдясно с инверсната матрица (по уговорка означена с): 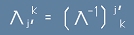 ;
;
Оказа се, че примовият базис се получава чрез умножение по инверсна на Лоренцовата матрица,
която преобразува векторите:
 .
.
Логично е да очакваме, че метричният тензор за примовия базис
ще се отклони от Тензорът на Минковски (виж Матрицата II) и ще има числени стойности плавно вариращи
встрани от -1,1,0 заедно с параметъра на трансформацията (параметърът е скоростта на примовата к.с.).
Ковариантни вектори
Илюстрацията на фиг.5 напомня постановката от
Матрицата I,
в която при същите обстоятелства дефинирахме дуален базис, за да е възможно пресмятането
на скаларни произведения. Пространството на Минковски, определено по-горе има псевдоортогонален характер
и помощните обръщения към правоъгълен декартов базис от по-рано биха работили по аналогичен начин.
Дуализмът ще ни трябва, тъй като трансформациите на Лоренц водят до остроъгълен базис.
Този линк описва още веднъж дуалните базиси.
Докато сме в псевдо-правоъгълна обстановка, можем да дефинираме и инверсен -
контравариантен метричен тензор: 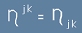 (дуален). В неправоъгълен базис ко- и контравариантният метричен тензор ще са различни,
но ще бъде спазено условието
(дуален). В неправоъгълен базис ко- и контравариантният метричен тензор ще са различни,
но ще бъде спазено условието 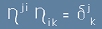 и с него ще можем да "вдигаме" индекси на векторите.
и с него ще можем да "вдигаме" индекси на векторите.
Нека в пространството има скаларно поле, например температура
F(x0,x1,x2,x3).
Частните производни на функцията F спрямо координатите
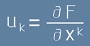 представляват компоненти на вектор U, наречен градиент на полето
представляват компоненти на вектор U, наречен градиент на полето  .
Възниква въпросът дали векторът U ще се преобразува по същия начин,
както вектора V от по-горе по формулата [6.1]?
Отговорът е не, защото компонентите на тази производна са всъщност отсечки отрязани върху
координатните оси и ще се преобразуват както самите координатни оси - по ковариантен начин.
.
Възниква въпросът дали векторът U ще се преобразува по същия начин,
както вектора V от по-горе по формулата [6.1]?
Отговорът е не, защото компонентите на тази производна са всъщност отсечки отрязани върху
координатните оси и ще се преобразуват както самите координатни оси - по ковариантен начин.
Така че градиентът е ковариантен вектор. Ковариантните вектори се представят в
базис, който е дуален спрямо основния, тоест съставен от контравариантни базисни вектори:
 .
.
По матричен начин това изглежда като
 , а по-кратко
, а по-кратко  .
.
Криво пространство
Умрял Владимир Илич Ленин и го пратили в ада.
След една седмица Сатаната се обажда на Бога:
- Моля те, прибери си го тоя! Накара дяволите да се организират в профсъюзи,
всичките малки дяволчета ги направи пионерчета, подстрекава грешните души да вдигат революция...
Взел го Господ в рая. След една седмица дяволът се обажда да пита какво става.
- Как е, Боже?
- Първо, казва се "Другарю Бог"! Второ, не ме занимавай сега, че бързам за партийно събрание. И трето - Бог няма!
(Стар виц)
 Криво пространсто няма.
Криво пространсто няма.
Понякога се среща фразата "изкривено пространство" (англ. curved space), или още "криволинейно пространство",
което е свързано с понятието за производна.
Имаме спомен за криволинейни - обобщени координати от една предна статия с подобна постановка.
Начинът по който имаме шанс да се ориентираме при незапазаващи се координадни оси е да си спомним три неща:
Първо: кривината е геометричен еквивалент на ускорението от физиката;
Второ: към всяка гладка линия можем да построим допирателна, която е права;
Tрето: разполагаме по наследство от Нютон и Лайбниц с диференциален апарат за плавен преход при гладки функции.
Имаме основание да мислим, че природните форми са гладки, затова този апарат е приложим.
Ако нещо прилича на пространство, но в него няма линейност/ортогоналност по координати
и не сме в състояние да го класираме по друг начин, то това нещо се нарича от математиката Многообразие.
Това е по-високо обобщение от пространствата с които сме свикнали да боравим.
Във всяка точка от многообразието можем да построим т.нар. котангентно пространство така, че координатните му оси
да бъдат допирателни към кривите - обобщените координати. Котангентно, защото, както предположихме по-горе,
осевите вектори в неправоъгълен базис са ковариантни. Дуално на котангентното е тангентното пространство,
в което пък се разполагат вектори и тензори - вече физически или геометрични обекти.
Кривата е израз на ускорението - променящата се скорост придава
променлив характер на Лоренцовите преобразувания, след което плоският модел, привързан към псевдо-декартовата схема
на Минковски, е приложим само в малък участък - клонящ към допирната точка.
Епилог
Думата "допирателна" е геометрична асоциация на понятието производна.
Начинът, по който се преобразуват производните изисква
специално разглеждане и води до термина "Ковариантна производна", разгледан в една от следващите статии.
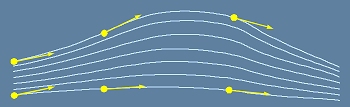 Липсата на кривина (тоест ускорение), в пространство-временните диаграми се изобразява с права (фиг.5).
В декартови условия сме свикнали да гледаме на правата като на стабилно множество, спрямо което важи
например сравнение от типа "успоредност", но в криволинейни координати прилагателното "успоредно" няма
същия смисъл. Сравнение или друга операция с два вектора има смисъл само ако двата вектора са от едно и също
допирателно пространство. Не е възможно да кажем дали два вектора в нелинейно многообразие са успоредни,
освен ако предефинираме какво означава това:
Има специален тип преобразувание, при което, макар компонентите на вектора да варират,
се запазва нулева стойност за ковариантната производна на нашия вектор спрямо някакъв път y=y(xj).
Такова преобразуване се нарича "успоредно пренасяне" - също предмет на по-късна статия.
Липсата на кривина (тоест ускорение), в пространство-временните диаграми се изобразява с права (фиг.5).
В декартови условия сме свикнали да гледаме на правата като на стабилно множество, спрямо което важи
например сравнение от типа "успоредност", но в криволинейни координати прилагателното "успоредно" няма
същия смисъл. Сравнение или друга операция с два вектора има смисъл само ако двата вектора са от едно и също
допирателно пространство. Не е възможно да кажем дали два вектора в нелинейно многообразие са успоредни,
освен ако предефинираме какво означава това:
Има специален тип преобразувание, при което, макар компонентите на вектора да варират,
се запазва нулева стойност за ковариантната производна на нашия вектор спрямо някакъв път y=y(xj).
Такова преобразуване се нарича "успоредно пренасяне" - също предмет на по-късна статия.
коментари
Радостин Желязков 27.09.2010
________________________________________________________________________________________
учебни статии по физика
 Матрицата III - революция
Матрицата III - революция
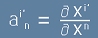 , тоест координатни преобразувания.
По един такъв преобразуващ елемент се полага на всеки индекс от тензора, съобразно типа му.
, тоест координатни преобразувания.
По един такъв преобразуващ елемент се полага на всеки индекс от тензора, съобразно типа му. .
Например метричният тензор може да се изрази като
.
Например метричният тензор може да се изрази като
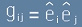 , а дуалният е
, а дуалният е 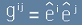 .
. Трансформации
Трансформации , или схематично
, или схематично  са базисни единични вектори в пространството на Минковски.
са базисни единични вектори в пространството на Минковски. , или по-кратко
, или по-кратко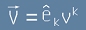 [6].
[6].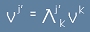 , или по-нагледно
, или по-нагледно
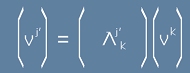 [6.1].
[6.1]. ,
или схематично
,
или схематично  .
.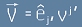 , или пък матрично
, или пък матрично и ако заместим от [6.1], получаваме
и ако заместим от [6.1], получаваме
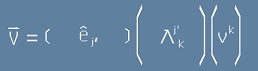 , тоест
, тоест [7].
[7].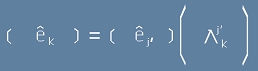 .
Да умножим отдясно с инверсната матрица (по уговорка означена с):
.
Да умножим отдясно с инверсната матрица (по уговорка означена с): 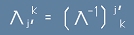 ;
; .
.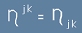 (дуален). В неправоъгълен базис ко- и контравариантният метричен тензор ще са различни,
но ще бъде спазено условието
(дуален). В неправоъгълен базис ко- и контравариантният метричен тензор ще са различни,
но ще бъде спазено условието 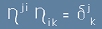 и с него ще можем да "вдигаме" индекси на векторите.
и с него ще можем да "вдигаме" индекси на векторите.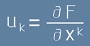 представляват компоненти на вектор U, наречен градиент на полето
представляват компоненти на вектор U, наречен градиент на полето  .
Възниква въпросът дали векторът U ще се преобразува по същия начин,
както вектора V от по-горе по формулата [6.1]?
Отговорът е не, защото компонентите на тази производна са всъщност отсечки отрязани върху
координатните оси и ще се преобразуват както самите координатни оси - по ковариантен начин.
.
Възниква въпросът дали векторът U ще се преобразува по същия начин,
както вектора V от по-горе по формулата [6.1]?
Отговорът е не, защото компонентите на тази производна са всъщност отсечки отрязани върху
координатните оси и ще се преобразуват както самите координатни оси - по ковариантен начин. .
. , а по-кратко
, а по-кратко  .
. Криво пространсто няма.
Криво пространсто няма. Липсата на кривина (тоест ускорение), в пространство-временните диаграми се изобразява с права (фиг.5).
В декартови условия сме свикнали да гледаме на правата като на стабилно множество, спрямо което важи
например сравнение от типа "успоредност", но в криволинейни координати прилагателното "успоредно" няма
същия смисъл. Сравнение или друга операция с два вектора има смисъл само ако двата вектора са от едно и също
допирателно пространство. Не е възможно да кажем дали два вектора в нелинейно многообразие са успоредни,
освен ако предефинираме какво означава това:
Има специален тип преобразувание, при което, макар компонентите на вектора да варират,
се запазва нулева стойност за ковариантната производна на нашия вектор спрямо някакъв път y=y(xj).
Такова преобразуване се нарича "успоредно пренасяне" - също предмет на по-късна статия.
Липсата на кривина (тоест ускорение), в пространство-временните диаграми се изобразява с права (фиг.5).
В декартови условия сме свикнали да гледаме на правата като на стабилно множество, спрямо което важи
например сравнение от типа "успоредност", но в криволинейни координати прилагателното "успоредно" няма
същия смисъл. Сравнение или друга операция с два вектора има смисъл само ако двата вектора са от едно и също
допирателно пространство. Не е възможно да кажем дали два вектора в нелинейно многообразие са успоредни,
освен ако предефинираме какво означава това:
Има специален тип преобразувание, при което, макар компонентите на вектора да варират,
се запазва нулева стойност за ковариантната производна на нашия вектор спрямо някакъв път y=y(xj).
Такова преобразуване се нарича "успоредно пренасяне" - също предмет на по-късна статия.