 Матрицата II - презареждане
Матрицата II - презареждане
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I.
Вижте какво пише в сайта на Станчо Павлов
за множествата.
Числовото множествата споменавано по долу би трябвало да е класирано като поле -
вижте дефиницията за поле
от Станчо Павлов.
Приблизително казано, това е група спрямо две действия - събиране и умножение.
Освен това искам да припомня, че се интересуваме живо от недекартови,
наречени по-рано остроъгълни координатни системи.
Умножение
Може да сме свикнали да гледаме на умножението като познато действие,
но нека преразгледаме значението на тази дума.
Като смисъл "умножение", дори за числа, не е толкова просто нещо. Освен това навиците, които имаме и смятаме за
полезни, може да ни подведат в някои случаи, които иначе в математиката са добре описани, или какъвто е случая с ОТО.
Да разгледаме фразата
ab = c.
Предполагат се две [съвпадащи едно с друго числови] множества от които са взети двата елемента
a b ;
Предполага се операция върху тях
f
- начин за извличане на резултата, съответствуващ на думата "умножение";
Предполага се резултат от операцията
c - елемент от [същото числово] множество.
Формално, това се нарича изображение (функция, англ. "map") и се означавана като
f:(A,B) -> C
където
f
е името на функцията;
A B
са означения за множествата - аргументи;
C
е множество към което принадлежи резултата /наричан още образ на функцията/. Когато
A,B,C
са числа, това е частен случай - числова функция с два аргумента.
В компютърните езици понякога има ясен аналогичен запис - чрез декларацията на подпрограма, която връща резултат:
"function c (a,b:real) :real;" или в друг вариант
"float c (float a,b);"
Сега записът от по-горе
"ab = c"
изглежда така:
f(a,b)=c ,
при което елементите
a b c
изобщо са разнородни и принадлежат на
множествата
A B C .
Ето няколко примера:
Нека
R
е множеството от реални числа.
- Числовото умножение се записва като
f:(R,R) -> R
Нека
V
е множеството от 3-мерни вектори.
- Векторно умножение се записва като
fv:(V,V) -> V
Нека
M33
е множеството от матрици с по 3 реда и 3 колони.
- Матричното умножение се записва като
- fmm:(M33,M33) -> M33
Сега да допуснем, че
M31
е множеството от 3x1 матрици, а
M13
е множеството от 1x3 матрици.
Тогава се дефинират различни умножения:
-
fCM:(M33,M31) -> M31
(матрица по вектор-стълб - във вектор-стълб)
-
fRM:(M13,M33) -> M13
(вектор-ред по матрица - във вектор-ред)
-
fVI:(M13,M31) -> R
(вектор-ред по вектор-стълб - в число - вътрешно произведение /от англ. inner product/)
-
fVO:(M31,M13) -> M33
(вектор-стълб по вектор-ред - в матрица - външно произведение /от англ. outer product/)
Да се обърнем пак към векторите.
Ако бяхме в правоъгълно пространство, можехме да дефинираме скаларно умножение на два вектора като
fs:(V,V) -> R.
Но виждайки двете възможни подредби при
M31
и
M13,
които са съставени от числова троица - тоест идентични с вектор обекти,
забелязваме само една версия на (вектор-ред,вектор-стълб) - в число:
M13xM31.
Тази версия - вътрешно произведение е известна още под името скаларно произведение на два вектора.
На същото основание скаларното умножение беше разглеждано в предната статия като операция без пряка
Симетрия
Ако a b са еднородни, тоест са от едно и също множество и
f(a,b) = f(b,a),
казваме, че функцията
f
е симетрична спрямо двата аргумента
a b.
При умножение на два еднородни аргумента симетрията се нарича още комутативност. Очевидно числовото умножение
е комутативано, а матричното и векторното произведение - не. Но какво да кажем за скаларното умножение?. Нека си спомним за думата
Разстояние
При скаларното произведение на два вектора дефиницията
fs:(V,V) -> R
работи само в декартови координати. Пак там разстоянието се пресмята по питагоровата теорема:
s2 = x2+y2+z2.
Но измежду гореописаните умножения няма нито едно, в което двата аргумента са еднородни вектори.
В предната статия дефинирахме специален взаимен базис /дуално пространство/, за да уредим този проблем.
След като премахнем декартовия случай, разстоянието (дължината на вектора) може да се опише само с такъв дуализъм -
свързан с метриката, или с други думи:
Векторът трябва винаги да е представен в два взаимни базиса, които по принцип са РАЗЛИЧНИ МНОЖЕСТВА.
Ясно е, че написаното по-горе декартово разстояние няма да работи за нашия случай, тъй като действието
x2 + y2 + z2 не е никак определено извън
Правоъгълни координати
От казаното по-горе личи, че отклонението от декартовата координатна система води до
невъзможност да представим разстоянието по начин съвместим с правилото "ред по стълб" за матрично умножение,
което иначе, в правоъгълни координати работи.
Но нашата представа за пространство се влияе силно от
нареченото по-горе "разстояние" и за което виждаме несъвместимост от две различни гледни точки -
едната е декартовата геометрия, другата е матрична, тоест математически "абстрактна".
Изглежда техническите трудност при
определянето на скоростта на светлината
са довели до грубото предположение, че тя е безкрайна. Най-вероятно затова правоъгълната координатна система
царува дълго време в нашите представи. Правоъгълна означава "линейно независима", тоест
когато си представяме как би изглеждала картината пред очите ни от друго място и под друг ъгъл, мислено допускаме,
че можем да идем и да проверим предположението си по неограничено бърз начин
(това включва и илюзията за едновременност), което не е вярно.
Крайната скорост на светлината е причина да преразгледаме и всичко видимо, тъй като то идва при нас не веднага,
а след време
t = x/c
- повече от секунда от Луната до Земята.
Тези проблеми имат връзка с (и може би идват от) обясненията, защото при предаването на знания сме свикнали да рисуваме нещата върху плоскост
- чрез прави линии и окръжности - пак по декартов път.
Това ни принуждава да се замислим доколко е правдива нашата
 Сетивност
Сетивност
1. Веднъж вече се срещнахме с логическите изводи от въображаемия
часовник на Файнман.
Те показаха, че времето и разстоянията имат връзка, тоест не са линейно независими.
Това автоматично означава,
че всички нарисувани графики на функцията
x = x(t)
в координатни двойки оси върху хартия, които сключват прав ъгъл, носят дефект. Този дефект е
малък, защото ако скалата
x
е в метри, а времето
t
- в секунди
(такива мерки са съответни на сетивността ни),
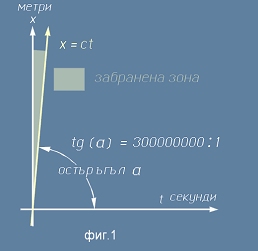
то графиката на функцията
x = ct
почти съвпада с ординатата и декартовата деформация е твърде малка (виж фиг.1).
2. Пак в статията за Файнман може би се забелязва една странна трудност - и за времето, и за дължината е казано,
че се скъсяват, но ако времето "там" тече по-бавно, някои биха се противопоставили
- самият израз "по-бавно" се асоциира със "закъсняване" и
може да се спори дали не е по-близо до "разширяване" отколкото до "скъсяване".
3. Тези две неща - първо острият ъгъл между оста
t
и правата
x = ct,
над която няма нищо, и второ - обратната асоциация на
времето /скъсяване - закъснение/, помагат да разберем защо е по-добре да ползуваме не декартово, а друго - специално построено и наречено
Пространство на Минковски
Пространството на Минковски е четиримерно и се описва от четири координатни оси - една за време:
ct,
и още три пространствени:
x y z,
затова се казва и пространство-време. То се състои от точки с координати
x y z ct. Тези точки се наричат събития и
могат да се тълкуват като вектори, наричани още четиривектори.
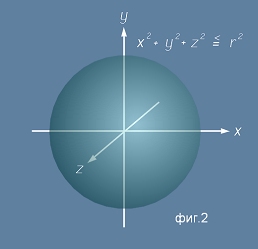
Ако декартовата сфера е геометрично място на точки, равноотдалечени от центъра - фиг.2 :
x2 + y2 + z2 - r2 = 0
[1],
то в пространство-времето на Минковски не е точно така.
Вземайки предвид, че
r
не може да превишава
ct,
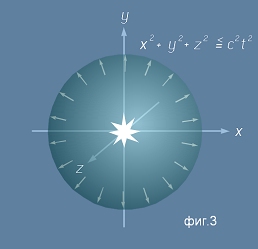
съобразяваме, че всичко възможно е вътре в едно кълбо - виж фиг.3, ограничено от равенството :
x2 + y2 + z2 - c2t2 = 0
[2].
На пръв поглед [1] и [2] са почти еднакви записи.
Обаче между тях има съществена разлика:
уравнението [1] описва форма според геометрия, идваща от правоъгълната представа, а
уравнението [2] описва геометрия според форма - такава форма, каквато можем само да опитаме да си представим,
например като фронт на светлинната вълна при явлението "блясък". Тази форма никак не е видима
- ни отвътре, ни отвън - фиг.3 е чисто въображаема рисунка.
Така, че [2] има характер на дефиниция, а не следствие.
Удобството на декартовите координати е, че в тях дължината - разстоянието между две точки - се запазва при трансформация.
В пространството на Минковски се запазва друго нещо, наречено интервал - интервалът се определя като:
s2 = x2 + y2 + z2 - c2t2.
[3]
От [3] е ясно, че това нещо - интервалът - трябва да е винаги отрицателен или в краен случай нула.
Но ние можем да го определим и като положителен, ако умножим по минус единица уравнението [2]:
c2t2 - x2 - y2 - z2 = 0.
[4]. Така интервалът става
s2 = c2t2 - x2 - y2 - z2
[5] и винаги трябва да е положителен, или нулев.
Лоренцовите преобразувания променят декартовото разстояние, но запазват интервала от [3] / [5] в пространство-времето на Миновски.
И наистина, почти преписвайки едномерните примове от
"Часовникът на Файнман", получаваме квадратите за ct' и x'
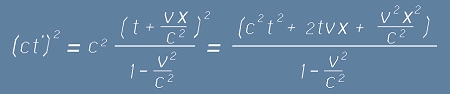 , после
, после 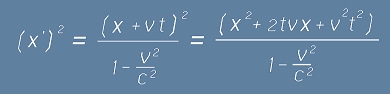
и виждаме, че 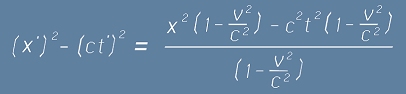 , което е интервала на Минковски.
, което е интервала на Минковски.
В пространство-времето на Минковски всяка точка (тоест всяко събитие)
има своя временна координата. Ако разглеждаме тези събития, за които пространствените координати
(x y z)
не се променят,
виждаме, че интервала между началото на к.с. и тях е нулев.
Нулевият интервал между две точки означава ход на светлинен лъч между тях. Това го нарекохме синхронизиране
на часовниците от двете к.с. в статията "Часовникът на Файнман". В този случай
x2 + y2 + z2 = c2t2.
Ето как се оказва, че всички фиксирани по
(x y z)
точки при Минковски се движат със скоростта на светлината.
Но ако това е вярно, всеки привидно "стоящ" предмет с маса
m
би притежавал огромна енергия.
Тук намираме сходство с известната формула
E = mc2
- виж равенство [7] от по-късна статия със заглавие "материя".
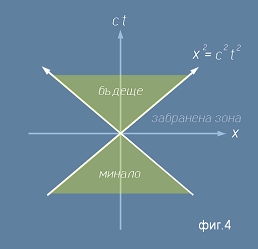
Пространствено-времена диаграма
Ние не можем да си представим образ в четири измерения, още по малко такъв може да се нарисува върху
плоскост.
Но на хартия или на плосък екран може да се изобразят двойка координатни оси, от които едната е пространствена (x),
а другата - временна (ct) - виж фиг.4.
Мащабите за ct и x са подбрани като приблизително равни - в светлинни секунди, за да се виждат ясно областите на бъдеще,
минало и невъзможната (забранена) зона. Наблюдателят се намира в центъра на координатната система.
Това изображение се нарича пространствено временна диаграма.
Приемането на равен мащаб за пространствената и временната ос улеснява
възприемането на явления с този мащаб.
За същото ставаше дума и в статията за Файнман, когато казахме, че естествената мярка за
дължина трябва да е светлинната секунда. Това означава да приемем, че скоростта на светлината е
c=1.
Тензор на Минковски
В статията "Матрицата I" видяхме как скаларното произведение в един базис се определя
чрез метричен тензор. Но дължината [на векторите] в пространството се получава като скаларното произведение, затова
често се казва, че метриката определя пространство.
Нека приемем, че c=1. В координати на пространство-времето на Минковски, ако индексираме направленията с 0,1,2,3 съотвени на
ct, x, y, z, метричният тензор се означава с гръцка малка буква Ета и се определя като:
 - Нарича се тензор на Минковски
при координатни означения:
- Нарича се тензор на Минковски
при координатни означения: 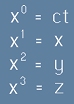 .
.
Да си спомним как изглежда скаларното произведение на два вектора U V от статията "Матрицата I":
UV = gjk Uj Vk.
По същия начин се пресмята и дължината и на един вектор:
V2 = gjk Vj Vk,
където с
gjk
означихме метричният тензор - в декартови или остроъгълни координати.
Аналогично, скаларното произведение на два четиривектора U V в пространството на Минковски е 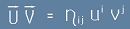 .
.
Интервалът [3] на Минковски се записва като 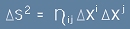 .
.
коментари
Радостин Желязков 26.09.2010
________________________________________________________________________________________
учебни статии по физика
 Матрицата II - презареждане
Матрицата II - презареждане
 Сетивност
Сетивност

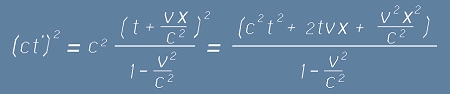 , после
, после 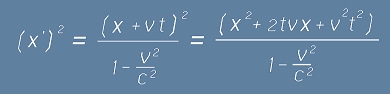
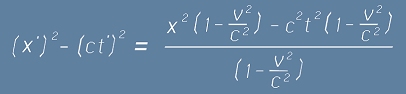 , което е интервала на Минковски.
, което е интервала на Минковски.
 - Нарича се тензор на Минковски
при координатни означения:
- Нарича се тензор на Минковски
при координатни означения: 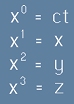 .
.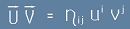 .
.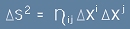 .
.