 Материя
Материя
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Предните (по време) статии са:
Матрицата I,
Матрицата II,
Матрицата III,
Ковариантна производна на вектор,
Символи на Кристофел,
Теорема на Ричи,
Успоредно пренасяне,
Кривини,
Производна на Ли,
Геодезично отклонение.
Плосък случай
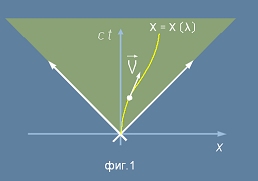 Да разгледаме път
Да разгледаме път 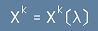 - жълта линия в диаграмата на Минковски - фиг.1
- непрекъсната поредица събития.
В статията "Матрицата II" интервалът на Минковски беше определен като
- жълта линия в диаграмата на Минковски - фиг.1
- непрекъсната поредица събития.
В статията "Матрицата II" интервалът на Минковски беше определен като
 .[1]
.[1]
Пак там видяхме, че знакът на интервала може да варира по определение като отрицателен или положителен.
Затова в [1] означението "на втора степен" в лявата страна е чисто дефинитивно и не бива да се приема като знак за действие.
Но след като сме избрали сигнатура (-1,1,1,1), знакът на [1] ще е отрицателен и затова
нека определим за реалните събития (цветният триъгълник на фиг.1) безконфликтна версия:
 .[2]
.[2]
Означеното с малка гръцка буква тау в ляво се нарича
Собствено Време
То съвпада с измереното локално време, съответно на интервала.
Допирателният вектор към този път
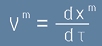 .[3]
.[3]
се нарича 4-скорост. Съпоставката на [3] и [2] показва, че
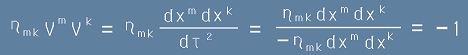 .[4]
.[4]
Тоест този вектор винаги е с една и съща "дължина" и тя е точно равна на минус единица.
За същото ставаше дума и в статията "Матрицата II", когато споменахме, че всички фиксирани точки
в пространство-времето се движат със скоростта на светлината, така, че "единицата" по-горе съответвува на скорост на светлината c=1.
Да допуснем, че по пътя се движи тяло с маса m (в покой - нарича се още Собствена Маса).
По определение, четиривекторът с компоненти
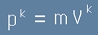 [5], се нарича
[5], се нарича
Четиривектор на Импулса
За неподвижно тяло само първата му компонента е ненулева и е равна на mc. Да допуснем, че тялото се движи по оста x със скорост v.
Тогава компонентите са други - съгласно Лоренцовите преобразувания, те ще се променят до
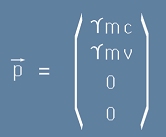 , където с малка гръцка буква гама е означен множителя на Лоренц:
, където с малка гръцка буква гама е означен множителя на Лоренц:
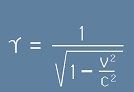 .
.
Сега ще дефинираме "друг" вектор
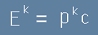 . [6]
. [6]
и ще го наречем
Четири-Енергия.
Да забележим, че след като множителят c=1, този вектор, като числен състав е неразличим
от четири-импулса.
Що се отнася до разликата в мерките - и такава няма - защото трябва да се съгласим,
че самата скорост на светлината е безразмерна единица, след като сме в Пространство-Времето на Минковски.
Постоянната дължина на 4-скоростта, записана в [4], определя постоянство и за 4-импулса, което гарантира закона за запазване на импулса,
а по смисъла на [6] - и на 4-енергията. Но да не забравяме, че разглеждаме плосък случай, тоест допирателно пространство.
Компонентата с индекс нула от четири-енергията за тяло в покой изразява известната формула:
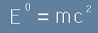 . [7]
. [7]
Внимание! Това е недостиг на означения. В лявата страна на [7] имаме горен тензорен индекс 0, а в дясната двойката е знак за втора степен.
И в следващите няколко формули, малките горни двойки означават степенуване.
Да обърнем внимание какво се случва със [7] при ненулева скорост. Тогава гама-множителят е съществен:
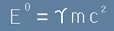 . [8]
. [8]
Следователно за материална точка при движение със скорост, v енергията като число е:
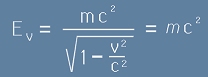 , [8.1]
, [8.1]
където с наклонена буква m е означена масата за движение със скорост v:
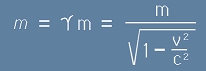 . [8.2]
. [8.2]
Второто равенство от [8.1], умножено по знаменателя и повдигнато на квадрат води до
 . [8.3]
. [8.3]
Да означим с P=mv импулса. Виждаме, че последният член от [8.3] е
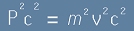 . [8.4]
. [8.4]
Заедно трите [8.1], [8.3], [8.4] показват, че
 . [8.5]
. [8.5]
Последното равенство [8.5] е важно и се ползува на други места.
В него, отляво Ev е енергията на тялото; в дясно m е масата в покой, а P е импулса.
То изразява връзката между енергия и импулс за материална точка в Теорията на Относителността.
[Отклонение 1]
Функцията
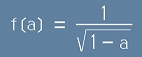 при малки стойности на аргумента
се представя в ред на Тейлор като:
при малки стойности на аргумента
се представя в ред на Тейлор като:
 . [9]
. [9]
Пак за малки стойности на аргумента, първата производна е
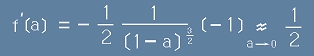 . [10]
. [10]
или, за аргументи близки до нула важи приближението  . [11]
. [11]
Ако съпоставим това с Лоренцовия фактор от по-горе при аргумент a = v2/c2 и заместим в [8], ще получим и
[Край на Отклонение 1]
Съпоставка с Нютон
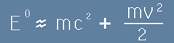 . [12]
. [12]
Фразата "тяло с маса m" означава материална точка.
За материя, разсеяна в пространството, се работи с по-висока по сложност абстракция, наричана
Тензор на Енергията
или понякога наричан Тензор на Енергия-Импулс, също и Тензор на Енергия-Напрежение.
(От англ. "energy-momentum tensor", "stress-energy tensor".
Думата "налягане", изполуваната по-долу, съответствува на нормална съставка на напрежението.)
Тензорът на Енергията се означава с
Tjk
и
по дефиниция е поток на
pj -
компонентата от четири-импулса през 3-мерна хиперповърхност определена от фиксирана координата
xk.
Ако с
Sk означим нормален 4-вектор към
една такава хиперповърхност, то тази дефиниция е еквивалент на равенството
TjkSk = pj. [13]
Да допуснем, че всички материални частици са в покой.
Нулевия компонент S0 е пространствения обем, а
T01,T02,T03 са нули,
защото при покой векторът на импулса е изцяло насочен по временната ос и не може да образува поток по пространствено направление.
От [13] остава T00S0 = p0.
p0 според [7] е енергията-еквивалент на собствената им маса.
Така че компонентата
T00
е енергийна плътност, приравнена чрез [7] към обикновена масова плътност.
В Нютоновата механика, налягането се измерва с
нютон / квадратен метър.
Тази единица се равнява на
килограм / (метър по секунда на квадрат),
тоест
[маса]/[дължина*време2].
При Минковски временните и пространствените мерки са едни и същи, затова горната единица се приравнява към
[маса]/[дължина3].
Това съвпада с единицата за плътност. Така, че плътност и налягане са
с еднакви размерности и съвпадат по смисъл.
Както видяхме по-горе в [7], масата и енергията също са с еднакъв смисъл, следователно
мярката за налягане може да се запише и като
[енергия]/[дължина3].
От [5] и [6] е ясно, че компонентите на импулса имат размерност на енергия (или маса).
Фразата "поток на импулс през 3-мерна хиперповърхност" може да се тълкува като масова плътност,
но и като налягане - обобщено до напрежение, ако системата не е в покой. От там идва названието "тензор на енергия-напрежение".
От там идва и симетрията на енергийния тензор.
Освен, че е симетричен, тензорът на енергията има нулева производна:
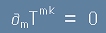 [14]
[14]
- което изразява законите за запазване на енергията (k=0) и импулса (k=1,2,3).
Това равенство може да бъде прието и като дефиниция за тензора на енергията
- тензор, съставен от компоненти с размерност енергия/обем и който се запазва.
коментари
Радостин Желязков 06.03.2011 / 17.09.2011
________________________________________________________________________________________
учебни статии по физика
 Материя
Материя
 Да разгледаме път
Да разгледаме път 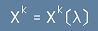 - жълта линия в диаграмата на Минковски - фиг.1
- непрекъсната поредица събития.
В статията "Матрицата II" интервалът на Минковски беше определен като
- жълта линия в диаграмата на Минковски - фиг.1
- непрекъсната поредица събития.
В статията "Матрицата II" интервалът на Минковски беше определен като .[1]
.[1] .[2]
.[2]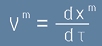 .[3]
.[3]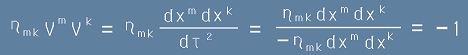 .[4]
.[4]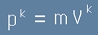 [5], се нарича
[5], се нарича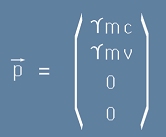 , където с малка гръцка буква гама е означен множителя на Лоренц:
, където с малка гръцка буква гама е означен множителя на Лоренц:
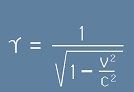 .
.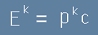 . [6]
. [6]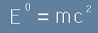 . [7]
. [7]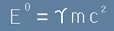 . [8]
. [8]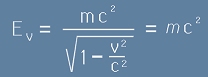 , [8.1]
, [8.1]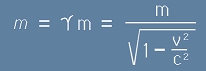 . [8.2]
. [8.2] . [8.3]
. [8.3]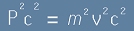 . [8.4]
. [8.4] . [8.5]
. [8.5]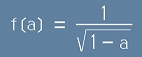 при малки стойности на аргумента
се представя в ред на Тейлор като:
при малки стойности на аргумента
се представя в ред на Тейлор като: . [9]
. [9]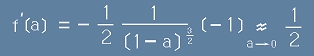 . [10]
. [10] . [11]
. [11]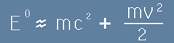 . [12]
. [12]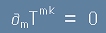 [14]
[14]