 Кривини
Кривини
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I, Матрицата II и Матрицата III.
Също и Ковариантна производна на вектор,
Символи на Кристофел,
Теорема на Ричи,
Успоредно пренасяне.
В статията "Успоредно пренасяне" получихме оценка за кривината изразена чрез Тензора на Риман:
 [1].
[1].
Сега ще покажем, че той е
Симетричен спрямо първа и втора двойка индекси.
Да разгледаме плоско допирателно пространство - метричният тензор
е един и същ навсякъде. Г-символите са нулеви, но не и производните им.
Тогава в тензора на кривината [1] ще останат само първите две съставки.
 [101].
[101].
За по-удобно представяне, нека "свалим" първия индекс на R:
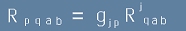 [102] , или като нов запис на [101]:
[102] , или като нов запис на [101]:
 . [103]
. [103]
Всеки от Гама-символите вдясно на [103] може да се изрази чрез метричния тензор,
както беше показано в [13] от статията "Символи на Кристофел".
Ако направим такова заместване и ако вземем предвид, че за плоско пространство
 ,
,
двата члена в скобите от дясната страна на [103] ще бъдат
 [104] и
[104] и
 . [105] ,
. [105] ,
Средните събираеми в [104] и [105] ще имат нулев ефект - понеже производните комутират, след което - като еквивалент на [103] можем да запишем:
 , или още по-кратко:
, или още по-кратко:
 . [106]
. [106]
Като имаме предвид, че реда в производните може да се размества и че метричния тензор е симетричен,
от последното равенство се разбира, че можем да разменим индексните двойки pq и ab, без това да промени резултата.
В началото предположихме, че разглежданото пространство е плоско. Но [106] е тензорно равенство,
следователно важи за всяка координатна система.
Следващата стъпка е да покажем едно важно равенство, наричано в книгите
Тъждество на Бианки
 . [107]
. [107]
Събираемите са ковариантни производни на Римановия Тензор и (погледнете [106])
в плоско допирателно пространство (тоест с нулеви Г-символи) биха изглеждали така:
 . [108]
. [108]
 . [109]
. [109]
 . [110]
. [110]
Горната тройка равенства наистина има нулев сбор - реда на диференциране е свободен, а метричният тензор е симетричен.
Отново ще се позовем на факта, че тензорното равенство [107], показано в една координатна система е в сила за всяка друга.
Да си спомним и подредим симетриите на тензора на Риман - от предната статия и тази по двойки индекси от [106]:
Rpqab = -Rpqba
Rpqab = -Rqpab
Rpqab = Rabpq.
Сумата от елементите по главния диагонал на една матрица се нарича Следа (англ. trace, понякога spur - шпур).
Ако елементите на матрицата са тензори, следата е също тензор, с две размерности по-малко от размерноста на
началния. Следата на тензора от [1], получена като контракция на индексите p a се нарича
Тензор на Ричи
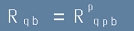 [2].
[2].
Макар да се означават с една и съща буква, тензорите от [1] и [2] се различават по тип (броя на индексите).
Ако приемем, че тензорът на Риман от [1] съдържа всички сведения за кривината, Тензорът на Ричи също носи
данни за кривината, но има по-малък брой елементи от [1]. Бидейки двумерна структура, тензорът на Ричи
има своя следа - вече число. Но ние не можем да правим направо контракция само по долните индекси q b, затова по-добре
да дефинираме смесен тензор - да вдигнем единия индекс чрез умножение по метричния тензор g:
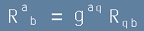 [3] ,
където вляво все още стои Тензорът на Ричи, но вече удобен за трасиране. Числото
[3] ,
където вляво все още стои Тензорът на Ричи, но вече удобен за трасиране. Числото
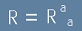 [4]
[4]
се нарича още
Скалар на Ричи
Това е числова оценка за кривината на пространството. Скаларът на Ричи е нулев за плоско пространство,
всъщност - погледнато отвътре - и за всяко друго, което се получава чрез обикновено (неразтегнато) огъване - например цилиндрична или конична повърхност.
В случай на равномерно движение по крива, кривината е вектор, съвпадащ с ускорението.
Да опитаме следата на тензора от лявата страна на [107]. Първо по индексите a c. Това значи да умножим с метричен тензор
gac. Да запишем трите събираеми:
 . [401]
. [401]
 . [402]
. [402]
 , [403]
, [403]
където във втората линия [402] нарочно разменихме първите два индекса,
за да направим контракция водеща до Тензора на Ричи.
Сега ще повторим още веднъж горната операция, но с индексите b q - умножаваме с
gbq - пак поотделно от горните три [401] [402] [403]:
 . [411]
. [411]
 . [412]
. [412]
 . [413]
. [413]
Да си спомним, че съгласно Бианки (по-горе), тези трите имат нулев сбор:
 [414] , или с по-кратък запис
[414] , или с по-кратък запис
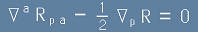 [415] .
[415] .
Тензорът на Айнщайн
се определя като
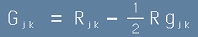 [5]
[5]
и сякаш нарочно е пригоден - като следствие от [415] - да спазва равенството
 .
.
коментари
Радостин Желязков 12.02.2011
________________________________________________________________________________________
учебни статии по физика
 Кривини
Кривини
 [1].
[1]. [101].
[101].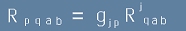 [102] , или като нов запис на [101]:
[102] , или като нов запис на [101]: . [103]
. [103] ,
, [104] и
[104] и . [105] ,
. [105] , , или още по-кратко:
, или още по-кратко: . [106]
. [106] . [107]
. [107] . [108]
. [108] . [109]
. [109] . [110]
. [110]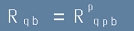 [2].
[2].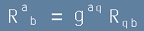 [3] ,
където вляво все още стои Тензорът на Ричи, но вече удобен за трасиране. Числото
[3] ,
където вляво все още стои Тензорът на Ричи, но вече удобен за трасиране. Числото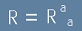 [4]
[4] . [401]
. [401] . [402]
. [402] , [403]
, [403] . [411]
. [411] . [412]
. [412] . [413]
. [413] [414] , или с по-кратък запис
[414] , или с по-кратък запис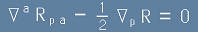 [415] .
[415] .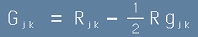 [5]
[5] .
.