 Символи на Кристофел
Символи на Кристофел
Този текст подпомага разбирането на математическия апарат в
Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I, Матрицата II и Матрицата III.
Статията Ковариантна производна дефинира за първи път Г-символите.
Криволинейно пространство
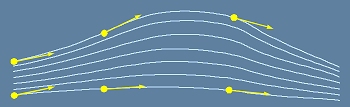 Ако векторите на координатния базис са допирателни към някакви гладки криви, тези криви могат да бъде разглеждани
като криволинейни координати, съставящи многообразие - "криволинейно" или обобщено пространство.
Ние можем да съпоставяме (тоест сравняваме, диференцираме, събираме) само такива вектори, които принадлежат
към допирателно пространство в една точка от многообразието. При преход от една към друга точка
се налага специална корекция, означавана с Г-символ (Гама символ, или Символ на Кристофел), осигуряваща
Ако векторите на координатния базис са допирателни към някакви гладки криви, тези криви могат да бъде разглеждани
като криволинейни координати, съставящи многообразие - "криволинейно" или обобщено пространство.
Ние можем да съпоставяме (тоест сравняваме, диференцираме, събираме) само такива вектори, които принадлежат
към допирателно пространство в една точка от многообразието. При преход от една към друга точка
се налага специална корекция, означавана с Г-символ (Гама символ, или Символ на Кристофел), осигуряваща
Плавен преход от базис в базис.
Символите на Кристофел се дефинират като
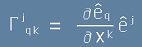 [1],
[1],
тоест те показват как се променят базисните вектори по направление на вектор с компоненти xk.
Ако пространството е 4-мерно, това е структура от 43=64 числа.
Г-символите са чисто геометрично изобретение.
Те не са тензори - това беше показано в статията ковариантна производна.
В същата статия обаче е показано как те компенсират нетензорната съставка при преобразуване
на производните между два съседни базиса. Сега ще покажем, че
Г-символите са симетрични по долните два индекса
- в случая q k: Да си спомним, че всеки вектор се изразява чрез компонентите си като
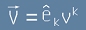 [2].
[2].
Базисните вектори не зависят от компонентите на V, затова можем да смятаме, че
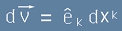 , или
, или 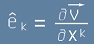 [3].
[3].
Можем да сменяме реда на диференциране, така, че от [1] и [3] се вижда :
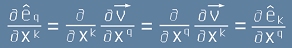 [4],
[4],
което показва, че Г- символите са симетрични по q и k - долните (десни) два индекса.
Г-символите от [1] се наричат още Символи на Кристофел от втори род. Има и
Символи на Кристофел от първи род,
те се дефинират по следния начин:
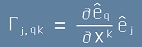 [5].
[5].
С тази дефиниция е удобно да намерим връзка между Г-символите и метричния тензор.
Използуваме симетрията по десните два индекса, показна по-горе в [4]:
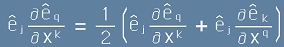 [6].
[6].
Да забележим, че 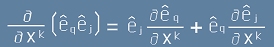 [7]
[7]
и следователно 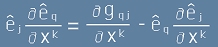 . [8]
. [8]
Аналогично 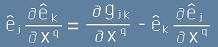 . [9]
. [9]
Да заместим [8] и [9] в [6]: получаваме 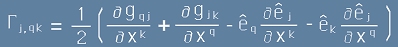 . [10]
. [10]
Последните два члена от [10] се преобразуват лесно пак поради симетрията, след което получаваме как точно
Г-символите се изразяват чрез метричния тензор:
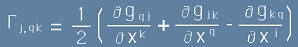 . [11]
. [11]
Да погледнем дефинициите [1] и [5]. След като знаем способността на метричния тензор да "вдига" и "сваля"
индекси, тоест 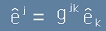 ,
,
виждаме и връзката между Гама-символите от първи и втори род:
 . [12]
. [12]
Така от [11] и [12] виждаме, че Г-символите от втори род се изразяват чрез метричния тензор като:
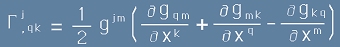 . [13]
. [13]
коментари
Радостин Желязков 29.10.2010
________________________________________________________________________________________
учебни статии по физика
 Символи на Кристофел
Символи на Кристофел
 Ако векторите на координатния базис са допирателни към някакви гладки криви, тези криви могат да бъде разглеждани
като криволинейни координати, съставящи многообразие - "криволинейно" или обобщено пространство.
Ние можем да съпоставяме (тоест сравняваме, диференцираме, събираме) само такива вектори, които принадлежат
към допирателно пространство в една точка от многообразието. При преход от една към друга точка
се налага специална корекция, означавана с Г-символ (Гама символ, или Символ на Кристофел), осигуряваща
Ако векторите на координатния базис са допирателни към някакви гладки криви, тези криви могат да бъде разглеждани
като криволинейни координати, съставящи многообразие - "криволинейно" или обобщено пространство.
Ние можем да съпоставяме (тоест сравняваме, диференцираме, събираме) само такива вектори, които принадлежат
към допирателно пространство в една точка от многообразието. При преход от една към друга точка
се налага специална корекция, означавана с Г-символ (Гама символ, или Символ на Кристофел), осигуряваща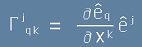 [1],
[1],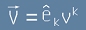 [2].
[2].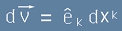 , или
, или 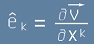 [3].
[3].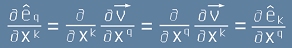 [4],
[4],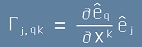 [5].
[5].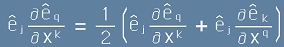 [6].
[6].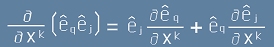 [7]
[7]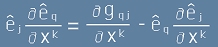 . [8]
. [8]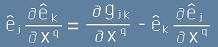 . [9]
. [9]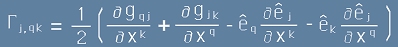 . [10]
. [10]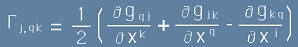 . [11]
. [11]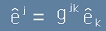 ,
, . [12]
. [12]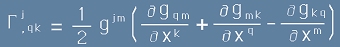 . [13]
. [13]