 Успоредно пренасяне
Успоредно пренасяне
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Трябва да сте гледали Матрицата I, Матрицата II и Матрицата III.
Важни са статиите Ковариантна производна на вектор,
Символи на Кристофел,
Теорема на Ричи.
Ковариантна производна на вектор по път
Да разгледаме път, тоест n-торка функции
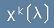 [1],
[1],
където k = 0..n-1, чиито аргумент е числото ламбда.
Векторът V, разгледан като сложна функция 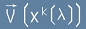 по този път ще има
ковариантна производна равна на
по този път ще има
ковариантна производна равна на
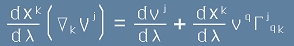 . [2]
. [2]
Ако тази производна е нулева, казваме, че векторът се пренася успоредно на себе си,
или - в условия на криволинейни координати - това е
Условие за успореден пренос
От [2] се вижда, че то е еквивалент на нулева ковариантна производна на V.
Сега ще докажем, че ако два вектора U V се пренасят успоредно, тяхното скаларно произведение се запазва.
Да приемем съкратено означение за израза от [2]:
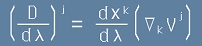 . [21]
. [21]
По същия път, скаларното произведение VU ще има ковариантна производна
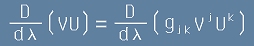 . [22]
. [22]
Ако погледнем подробния запис за дясната страна на [22] :
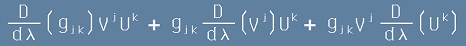 [23] ,
[23] ,
можем да твърдим, че и трите събираеми са тъждествено равни на нула -
първото - според вече описаната Теорема на Ричи, а второто и третото - според условието за успореден пренос в [2].
Това доказва, че при успореден пренос, скаларното произведение (следователно и дължината на пренасяния вектор) се запазва.
Да разгледаме вектор допирателен към пътя [1]. Той би имал компоненти
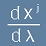 .
.
Имайки предвид [2], ковариантна производна на допирателния вектор ще бъде
 [3].
[3].
Изразът [3] заслужава особено внимание. Ако го сложим отляво на едно равенство, а отдясно на същото равенство пишем нула, ще получим прочутото
Геодезично уравнение
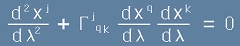 [4].
[4].
Път, който спазва това уравнение, се наричан геодезичен или геодезична линия. Ако многообразието клони към плоско пространство, второто събираемо ще изчезне и ще получим уравнение на права. На сферична повърхност такива линии са големите кръгове.
Геодезичните линии са базово понятие в разбирането за криволинейно многообразие. Ето един пример:
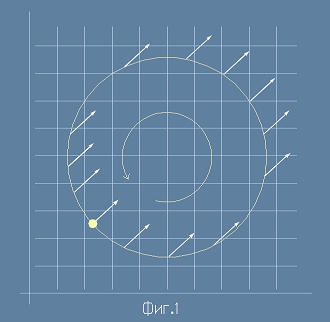
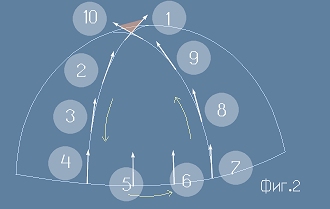 Опитвайки се да схвана що за явление е "успоредния пренос", разглеждах две рисунки, подобни на Фиг.1 и Фиг.2 - често представяни в литературата,
за да илюстрират разликата между плоско и криволинейно успоредно пренасяне.
Опитвайки се да схвана що за явление е "успоредния пренос", разглеждах две рисунки, подобни на Фиг.1 и Фиг.2 - често представяни в литературата,
за да илюстрират разликата между плоско и криволинейно успоредно пренасяне.
В плоско пространство ние сме свободни да гледаме на вектора като свободно плаващ навсякъде, запазвайки направлението и дължината си. Ако придвижим един вектор успоредно на себе си по някакъв затворен контур, в края на движението той ще съвпадне с началния си образ - виж Фиг.1.
В криволинейни координати обаче не можем да съпоставяме вектори, които са от различни тангентни пространства. Тоест за тях не е възможно да кажем дали са "успоредни" или "с равни големини".
Ако последователно правим успоредно пренасяне на един вектор по затворен път, в края на движението си
той няма да съвпадне със себе си, а ще бъде друг и ще зависи от пътя, по който е било извършвано движението - На Фиг.2 е изобразено такова движение върху сфера, в 10 позиции, което започва от полюса, стига до екватора,
придвижва се малко по екватора и обратно се връща в полюса. Позиции 1 и 10 показват началния и крайния вектор, които явно са различни. Този пример ми се стори малко неясен.
Очевидно по маршрута от Фиг.2 на полюса има "ръб", в който преносът вече не е гладък,
освен това съмнително съвпада с центъра в който се събират всички меридиани и там например
посоката "към екватора" е безсмислена. А какво би било, ако пътя не минава през полюса?.
Първият опит да си представя такъв път беше неуспешен -
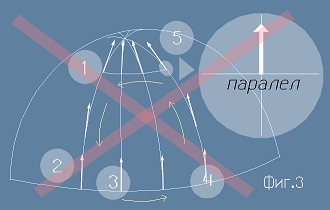
 стигнах до същия вектор, от който е започнало движението. (виж Фиг.3).
Но когато го погледнах отблизо, разбрах, че моето мислене се подвежда по
традиционната географска координатна мрежа, асоциирайки я с правоъгълна обстановка.
стигнах до същия вектор, от който е започнало движението. (виж Фиг.3).
Но когато го погледнах отблизо, разбрах, че моето мислене се подвежда по
традиционната географска координатна мрежа, асоциирайки я с правоъгълна обстановка.
В точка 5 аз си въобразявах, че векторът трябва да запази посоката на меридиана,
както и правия ъгъл, който векторът сключва с паралела - Грешка!
Сега разбрах какво ме подвежда -
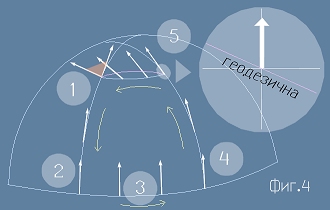
Грешката е: Aко нещо се запазва, то не е ъгъл между вектора и паралела, а по-скоро ъгълът между вектора и геодезичната линия, която в този случай е голям кръг.
На фиг.4 геодезичната линия е с виолетов цвят и никак не съвпада с паралела. Там се вижда,
че ако запазим ъгъла към нея, резултатът е същия, както на фиг.2, където маршрутът е действително
подбран така, че да минава по геодезични линии. Има доказателство,
че разликата между началния и крайния вектор зависи само от пространствения ъгъл,
който се образува от затворения контур.
Засега обаче е по-важно друго - че тази разлика може да послужи при оценката за
Кривина
на пространството. Най простата версия на затворен контур може да се определи от два вектора A и B - виж фиг.5.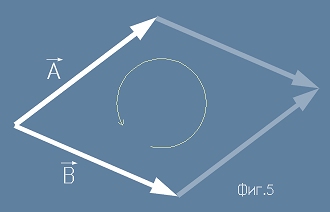
Когато затворения контур определен от тези два вектора намалява, кривината се стабилизира в ненулева
гранична стойност, която не зависи от избора на координатна система, но е свойство на самото пространство
и се изразява в това, че кой да е вектор V, обхождайки напълно този контур, ще се промени.
Да означим с 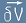 вариацията на V при вариации в дължините
вариацията на V при вариации в дължините
 на двата контурни вектора A и B.
на двата контурни вектора A и B.
Ще потърсим каква е зависимостта (преобразуванието)  .
.
Да предположим, че има тензор, с който става търсеното преобразувание.
Щом е преобразуващ тензор - от вектор към вектор - той трябва да има един ко и един контравариантен индекс.
Но този тензор определено ще зависи и от двата вектора A и B, така, че за да бъдат прихванати и те в преобразуванието, трябва търсеният тензор да има още два ковариантни индекса. Всъщност се събраха
един горен и три долни индекса, затова предполагаме, че вариацията ще е
 . [5]
. [5]
Тази формула е ориентировъчна. Няма да я доказваме, но от тук имаме идея, че съществува
тензор
Rpqab ,
който се нарича
Тензор на Риман
или просто тензор на кривината.
Както видяхме по-горе, ковариантната производна е мярка за това доколко пренасянето се
отклонява от успоредното (където тя е нулева). Видяхме също, че резултатът от преноса зависи от кривината.
Точна представа за тензора на кривината може да се получи, ако пресметнем комутатора (ab-ba)
на две последователно приложени ковариантни производни на един вектор V по две различни направления
(каквито са по-горе двата вектора A и B).
За яснота "как така комутаторът отмерва кривината", вижте статията Производна на Ли.
За съвместимост с написаното другаде, нека приемем означението 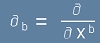 и да си спомним как би изглеждала с него
и да си спомним как би изглеждала с него
ковариантната производна за смесен тензор от тип (1,1) -
виж [98] от статията Теорема на Ричи:
 .
.
Комутаторът, споменат по-горе се записва като:
 . [6]
. [6]
Да пресметнем поотделно първия и втория член от [6]:
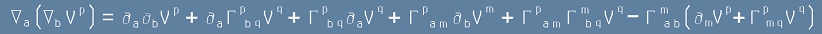 . [7]
. [7]
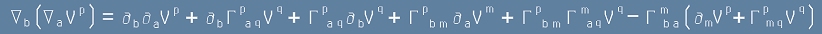 . [8]
. [8]
Първият и последният член на двата израза в дясно на [7] и [8] са симетрични по двата индекса a b и
значи няма да участвуват в разликата; Третият член от [7] ще се унищожи от четвъртия член на [8],
а четвъртият от [7] - с третия от [8]. Комутаторът е
 . [9]
. [9]
А търсеният тензор - тензор на Риман представлява:
 . [10]
. [10]
Този тензор е построен чрез две двойки вектори
- първата двойка са началната и крайната версия на вектора V при движението по затворения контур.
Ясно е, че ако им разменим местата (тоест разгледаме същото движение в обратна посока),
трябва да получим същата по големина промяна, но с отрицателен знак,
по правилото a-b = - (b-a). Следователно имаме антисиметрия по преобразуващите индекси (първите два).
Отделно от това, Комутаторът [6] също показва, че
ако разменим местата на двата вектора a b трябва да получим същия по големина резултат с отрицателен знак.
Това говори, че Тензорът на Риман е антисиметричен и по последните два индекса:
Rpqab = -Rpqba
Rpqab = -Rqpab
коментари
Радостин Желязков 05.12.2010
________________________________________________________________________________________
учебни статии по физика
 Успоредно пренасяне
Успоредно пренасяне
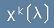 [1],
[1],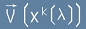 по този път ще има
ковариантна производна равна на
по този път ще има
ковариантна производна равна на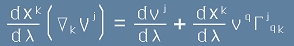 . [2]
. [2]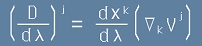 . [21]
. [21]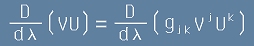 . [22]
. [22]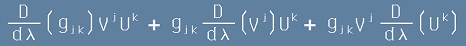 [23] ,
[23] ,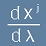 .
. [3].
[3].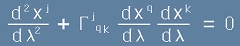 [4].
[4].
 Опитвайки се да схвана що за явление е "успоредния пренос", разглеждах две рисунки, подобни на Фиг.1 и Фиг.2 - често представяни в литературата,
за да илюстрират разликата между плоско и криволинейно успоредно пренасяне.
Опитвайки се да схвана що за явление е "успоредния пренос", разглеждах две рисунки, подобни на Фиг.1 и Фиг.2 - често представяни в литературата,
за да илюстрират разликата между плоско и криволинейно успоредно пренасяне.
 стигнах до същия вектор, от който е започнало движението. (виж Фиг.3).
Но когато го погледнах отблизо, разбрах, че моето мислене се подвежда по
традиционната географска координатна мрежа, асоциирайки я с правоъгълна обстановка.
стигнах до същия вектор, от който е започнало движението. (виж Фиг.3).
Но когато го погледнах отблизо, разбрах, че моето мислене се подвежда по
традиционната географска координатна мрежа, асоциирайки я с правоъгълна обстановка.
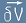 вариацията на V при вариации в дължините
вариацията на V при вариации в дължините
 на двата контурни вектора A и B.
на двата контурни вектора A и B. .
. . [5]
. [5]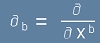 и да си спомним как би изглеждала с него
и да си спомним как би изглеждала с него .
. . [6]
. [6]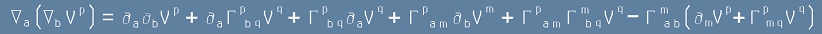 . [7]
. [7]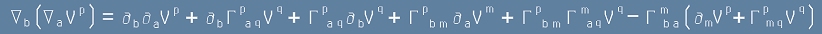 . [8]
. [8] . [9]
. [9] . [10]
. [10]