 Производна на Ли
Производна на Ли
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Предните (по време) статии са:
Матрицата I,
Матрицата II,
Матрицата III,
Ковариантна производна на вектор,
Символи на Кристофел,
Теорема на Ричи,
Успоредно пренасяне,
Кривини.
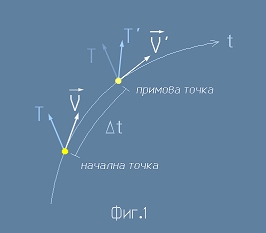
Тази статия има за цел да покаже как комутаторът ab-ba измерва кривината.
Съпоставят се реално пренесен по кривата тензор (наречен по-долу примов) и плоска екстраполация на същия тензор, получена
като развивка в ред на Тейлор.
 Да си представим линия с координати
Да си представим линия с координати 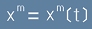 [1]
[1]
- където t е числов параметър - дължина; Да си представим също и векторно поле V(x) - такова,
че във всяка точка векторът V е допирателен към линията, имайки координати
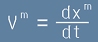 . [2]
. [2]
Нека има някакъв тензор T = T(V), който се променя при движение по същата линия.
Да разгледаме пренос върху малък участък от кривата - V ще се преобразува до V ',
а T ще се преобразува до T '.
Производната на Ли за тензор T спрямо векторното поле V се дефинира като
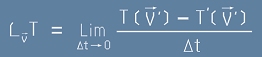 . [3] *
. [3] *
Това би било нула при движение по права - следователно отразява изкривяването, видимо от фигурата.
Ще потърсим поотделно изрази за двете съставки на числителя от дясно на [3]. Започваме с T '.
Съгласно [2], можем да напишем примовите координати като
 [4] ,
[4] ,
което иначе си е координатно преобразувание от вида  , с матрица
, с матрица
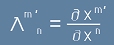 [5] .
[5] .
Съпоставката на последните две равенства [4] и [5] води до следния израз за ламбда-матрицата:
 [6] ,
[6] ,
където първото събираемо в дясно е делта-символа на Кронекер, тоест единичната матрица,
а второто - производната на вектора V според означение 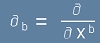 .
.
Да приемем за простота, че разглежданият тензор е обикновен вектор - един горен индекс.
В такъв случай - погледнете [6] - той ще се преобразува така:
 [7] .
[7] .
Дотук с втория член от числителя на [3]. Сега ще търсим израз за първия.
Началният тензор T може да се представи в примовата точка като сбор близък до [7], чрез ред на Тейлор
- разглеждайки примовата точка като близка до началната:
 , където последният член в скобите - o - е сбор
от бързо клонящи към нула малки събираеми, съдържащи степени 2 и повече. Изполувайки [2], получаваме
, където последният член в скобите - o - е сбор
от бързо клонящи към нула малки събираеми, съдържащи степени 2 и повече. Изполувайки [2], получаваме
 .
.
Според развивката на Тейлор:
 . [8]
. [8]
Замествайки [7] и [8] в дефиницията [3], виждаме, че
Производната на Ли за тензор T върху векторно поле V
се изразява с формулата:
 . [9] *
. [9] *
Дясната страна на [9] понякога се нарича комутатор на Ли.
*
Забележка:
Тук има особено означение - в левите страни на [3] и [9] индекса v не е координатен, а означава
посока по вектора V.
коментари
Радостин Желязков 26.02.2011
________________________________________________________________________________________
учебни статии по физика
 Производна на Ли
Производна на Ли
 Да си представим линия с координати
Да си представим линия с координати 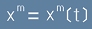 [1]
[1]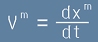 . [2]
. [2]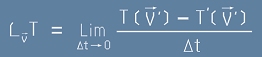 . [3] *
. [3] * [4] ,
[4] , , с матрица
, с матрица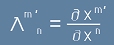 [5] .
[5] . [6] ,
[6] ,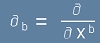 .
. [7] .
[7] . , където последният член в скобите - o - е сбор
от бързо клонящи към нула малки събираеми, съдържащи степени 2 и повече. Изполувайки [2], получаваме
, където последният член в скобите - o - е сбор
от бързо клонящи към нула малки събираеми, съдържащи степени 2 и повече. Изполувайки [2], получаваме .
. . [8]
. [8] . [9] *
. [9] *