 Преобразувание на Фурие-Обща версия
Преобразувание на Фурие-Обща версия
Това е клон от предната статия:
Преобразувание на Фурие.
От предната статия
са важни двете равенства
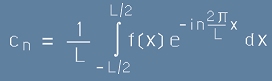 .[15]
.[15]
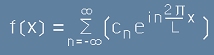 .[16]
.[16]
Дефиниции
Обща версия
Да дефинираме аргумент k, който съединява в едно двата L и n:
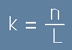 .[17.1]
.[17.1]
Щом периодът на повторение е L, тогава 1/L ще е единицата честота - най-малката възможна.
Да означим единицата честота с делта k:
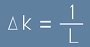 . [18.1]
. [18.1]
Нека приемем, че извън интервала -L/2 .. L/2 функцията f(x) има пренебрежимо
малка стойност.
Тогава границите на интегриране в [15] могат да се разпрострат от минус до плюс безкрайност.
Така, че [15] и [16] биха изглеждали като
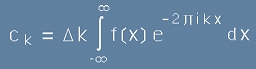 .[19.1]
.[19.1]
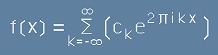 .[20.1]
.[20.1]
Да приемем също означението
 .[21.1]
.[21.1]
Тогава коефициентите Ck ще бъдат:
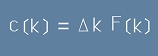 ,[22.1]
,[22.1]
a сборът [20.1] би трябвало да изглежда като
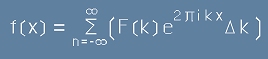 .[23.1]
.[23.1]
Получихме сбор, който лесно се превръща в интеграл
при реална стойност на k.
Така стигаме до вече известното
Преобразувание на Фурие
Твърдението "Ако
 , [24.1]
, [24.1]
то
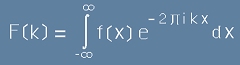 ." [25.1]
." [25.1]
се нарича Теорема на Фурие. Преобразуванието от [24.1] към [25.1] е Преобразувание на Фурие.
Както виждаме, за всяка функция f(x) от вида [24.1], се съпоставя друга, F(k), наричана Фурие-образ,
чрез [25.1].
Аргументната двойка k,x може да
се тълкува като ъглова честота - време, но също и като вълнов вектор - координата.
Радостин Желязков 23.10.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Преобразувание на Фурие-Обща версия
Преобразувание на Фурие-Обща версия
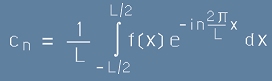 .[15]
.[15]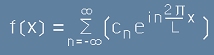 .[16]
.[16]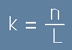 .[17.1]
.[17.1]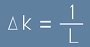 . [18.1]
. [18.1]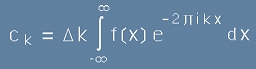 .[19.1]
.[19.1]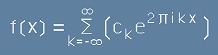 .[20.1]
.[20.1] .[21.1]
.[21.1]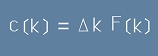 ,[22.1]
,[22.1]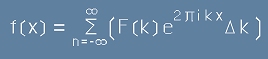 .[23.1]
.[23.1] , [24.1]
, [24.1]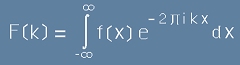 ." [25.1]
." [25.1]