 Преобразувание на Фурие
Преобразувание на Фурие
Това е помощна статия. Целта й е само запознаване с преобразуванието на Фурие,
без много подробности.
Полезни сведения свързани с тази тема има в страницата на Станчо Павлов:
Редове на Фурие.
Ред на Фурие
Да допуснем, че x е реална променлива, варираща в интервала
( ..
..
 ).
).
Тогава всяка функция f(x) може да бъде сведена
до безкраен сбор:
 , [1]
, [1]
известен под името Ред на Фурие.
Сега да си представим една друга, функция, близка по запис до горната:
 . [2]
. [2]
Тя е интересна, защото в скобите стои Ойлерово комплексно число, умножено по коефициент cn,
с други думи тя е еквивалент на:
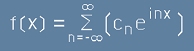 . [3]
. [3]
Да поставим тази функция в ролята на
Разпределение
и да пресметнем интеграла:
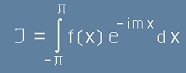 . [4]
. [4]
Съгласно [3], той ще е
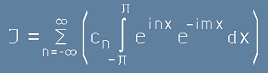 . [5]
. [5]
Да разгледаме подинтегралния израз
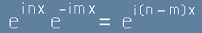 - той е равностоен на
- той е равностоен на
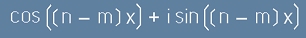 .[6]
.[6]
Сега да обърнем внимание на едно малко множество от
Интеграли
на тригонометрични функции, обстойно разгледани в посветена на тази тема
статия на Станчо Павлов.
Функциите sin(x) и cos(x) имат повтарящи се стойности на всеки 2пи от аргументната ос и
интегралите им във всеки интервал от 2пи са нулеви.
Ако аргументът x е умножен по ненулева константа c, това не се променя. Например при косинусова функция имаме
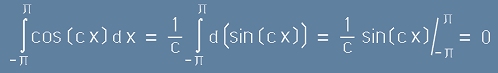 .[7]
.[7]
Подобно на [7] би изглеждал и интеграл от sin(cx) в интервала от минус пи до пи, ако c е различно от нула.
Обаче ако константата c е нула, 1/c не е определено и действието [7] не би било възможно.
В този случай, функцията косинус има стойност по целия интервал единица, а функцията синус е нула.
Интеграл от cos(0), при граници между минус и плюс пи, ще даде правоъгълник с височина 1
и основа 2пи.
Интеграл от sin(0), при всяко определено интегриране дава нула.
Следователно интегралът от [5] ще е
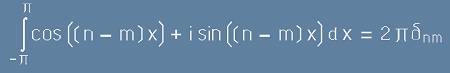 ,[8]
,[8]
където с делта е означен символа на Кронекер - той е нула при различни n и m, a при n=m е равен на 1.
И така, сборът J от [5] се свежда до
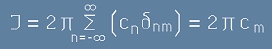 , тоест
, тоест
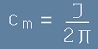 .[9]
.[9]
Индексът m в това равенство съответствува на m от [4]. Можем да го сменим на двете места с n.
Да заместим J от [4] в [9]. Ще получим израз за коефициентите Cn от [3]:
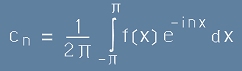 .[10]
.[10]
Да повторим по-горе записания сбор [3]:
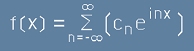 . [=3]
. [=3]
В тази двойка равенства, [10] и [=3], се вижда равновесие:
От една страна, функицията f(x) играе разпределяща роля в [10].
От друга страна, коефициентите Cn са разпределящи в сбора [=3].
Но да продължим. Погледнете равенството [10].
Внимание!. Ще "разтегнем" аргументната ос, така, че интервалът 2пи да се проектира върху нов,
с дължина L.
Значи да изместим променливата x с нова, y - такава, че:
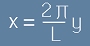 .[11]
.[11]
Ако функцията f(x) е периодична с интервал на повтаряне 2пи, то
същата функция, с новия аргумент y, е периодична с интервал на повтаряне L.
Това се вижда от пряко пресмятане:
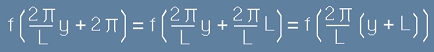 .[12]
.[12]
Думата "разтегнем" беше, защото тази нова функция, в интервала от -L/2 до L/2, заема същите
стойности, както старата f(x) в интервала от -пи до пи.
И така, равенствата [10] и [=3] се презаписват като
 ,[13]
,[13]
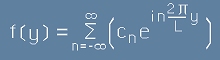 ,[14]
,[14]
Moжем да сменим обратно y с x - просто като означения, след което двойката [13] [14] ще има следния вид:
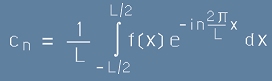 .[15]
.[15]
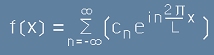 .[16]
.[16]
След всичко това, вече няма нужда да се ограничаваме в интервал 2пи.
Следващата стъпка е да направим няколко
Дефиниции *
Да дефинираме аргумент k, който съединява в едно двата L и n:
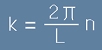 .[17]
.[17]
Щом периодът на повторение е L, тогава 1/L ще е единицата честота - най-малката възможна.
Да означим ъгловата версия на тази единица с делта k:
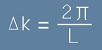 . [18]
. [18]
Нека приемем, че извън интервала -L/2 .. L/2 функцията f(x) има пренебрежимо
малка стойност.
Тогава границите на интегриране в [15] могат да се разпрострат от минус до плюс безкрайност.
Така, че [15] и [16] биха изглеждали като
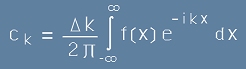 .[19]
.[19]
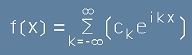 .[20]
.[20]
Да приемем също означението
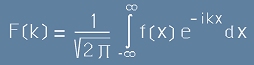 .[21]
.[21]
Тогава коефициентите Ck ще бъдат:
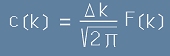 ,[22]
,[22]
a сборът [20] би трябвало да изглежда като
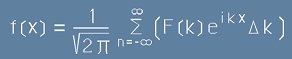 .[23]
.[23]
Получихме сбор, който лесно се превръща в интеграл
при реална стойност на k.
Така стигаме до обещаното в заглавието
Преобразувание на Фурие
Твърдението "Ако
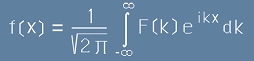 , [24]
, [24]
то
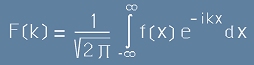 ." [25]
." [25]
се нарича Теорема на Фурие. Преобразуванието от [24] към [25] е Преобразувание на Фурие.
Както виждаме, за всяка функция f(x) от вида [24], се съпоставя друга, F(k), наричана Фурие-образ,
чрез [25].
Аргументната двойка k,x може да
се тълкува като ъглова честота - време, но също и като вълнов вектор - координата.
* Забележка
Последните две формули [24] и [25] имат друга, леко различна версия, описана в клон от предпоследната точка "Дефиниции".
Можете да погледнете и дубъл на целия текст, но с таблична съпоставка на двете версии.
Радостин Желязков 20.10.2011 .. последна редакция 23.10.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Преобразувание на Фурие
Преобразувание на Фурие
 ..
..
 ).
). , [1]
, [1] . [2]
. [2]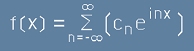 . [3]
. [3]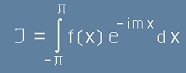 . [4]
. [4]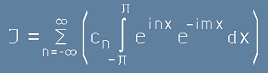 . [5]
. [5]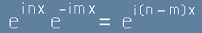 - той е равностоен на
- той е равностоен на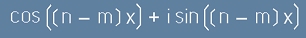 .[6]
.[6]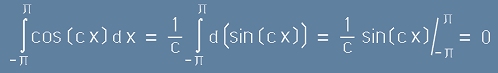 .[7]
.[7]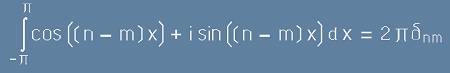 ,[8]
,[8]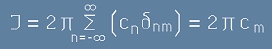 , тоест
, тоест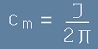 .[9]
.[9]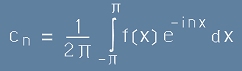 .[10]
.[10]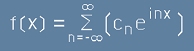 . [=3]
. [=3]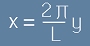 .[11]
.[11]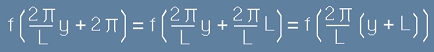 .[12]
.[12] ,[13]
,[13]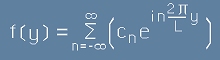 ,[14]
,[14]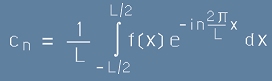 .[15]
.[15]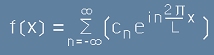 .[16]
.[16]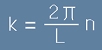 .[17]
.[17]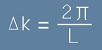 . [18]
. [18]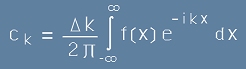 .[19]
.[19]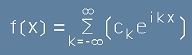 .[20]
.[20]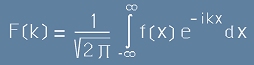 .[21]
.[21]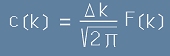 ,[22]
,[22]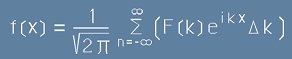 .[23]
.[23] , [24]
, [24]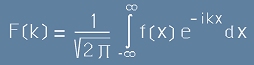 ." [25]
." [25]