 Соленоид
Соленоид
Това е част от класическата електромагнитната теория.
Трябва да сте запознати с:
Уравненията на Максуел.
Соленоидът по-долу е "идеален" - модел, чиято цел е да "затвори" магнитното поле в удобен за тълкуване
геометричен примитив. Технологичните бобини обикновено се отклоняват от него.
Соленоид
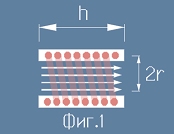 Практически това е синоним на бобина или намотка. Представлява навит проводник
във форма на цилиндър с дължина h и диаметър 2r (виж фиг.1). Дължината h на идеалния соленоид трябва да е много по-голяма
от диаметъра. При тези условия можем да смятаме, че магнитното поле е съсредоточено изцяло във вътрешността
на намотката. Соленоида има собствена характеристика, наречена
Практически това е синоним на бобина или намотка. Представлява навит проводник
във форма на цилиндър с дължина h и диаметър 2r (виж фиг.1). Дължината h на идеалния соленоид трябва да е много по-голяма
от диаметъра. При тези условия можем да смятаме, че магнитното поле е съсредоточено изцяло във вътрешността
на намотката. Соленоида има собствена характеристика, наречена
Индуктивност
Индуктивността се дефинира с формулата
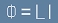 , [1]
, [1]
където Ф е магнитния поток, L е индуктивност,
I е електричния ток.
С думи това е коефициента, с който магнития поток е пропорционален на създаващия го електричен ток.
Производната по времето на двете страни в дефиницията [1],
заедно с формула [6] от статията "Уравнения на Максуел" - закона на Фарадей
за електромагнитната индукция, дават равенството
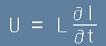 , [2]
, [2]
където U е индуцираното напрежение, I-създаващия ток, L е индуктивността.
Равенство [2] е еквивалент на [1], тоест може да служи и като дефиниция.
След като предполагаме, че цялото поле е вътре в соленоида,
интегралът [13] от статията Максуел ще бъде сведен до
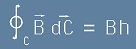 [3]
[3]
(в тази статия буквата L означава индуктивност, затова контура в [3] е означен с буква C).
Но това е дял само на една навивка. Ако означим с N0 броя на всички навивки,
за сборното поле важи
 . [4]
. [4]
Да въведем линейна гъстота на навивките
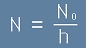 [5]
[5]
където N е брой навивки за единица от дължината h на соленоида,
от което следва формула за полето в соленоида:
 . [6]
. [6]
Всяка една навивка от соленоида ще бъде пронизвана от магнитен поток идващ от това поле:
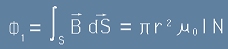 . [7]
. [7]
и промяната в този поток ще индуцира в нея напрежение (точно това напрежение се има предвид в дефиницията [2]).
Навивките са последователно свързани и напрежението, споменато в [2] за целия соленоид
ще е произведение на [7] по броя на всички навивки в бобината.
Ефективния магнитен поток през целия соленоид - виж [5] - ще бъде
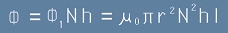 . [8]
. [8]
Ако погледнем горното развенство [8] и още малко по-горе, [1], виждаме, че
 , [9]
, [9]
където L е индуктивността на соленоида, r и h са радиус и дължината му, N е линейната гъстота на навивките.
Енергия на магнитното поле
Токът течащ по навивките на соленоида има магнитно и топлинно действие.
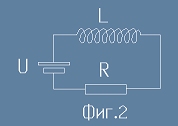 Схематично това се изобразява като последователно свързани индуктивност и съпротивление (виж фиг.2).
Напрежението на източника се разделя условно на две части - имайки предвид [2]
Схематично това се изобразява като последователно свързани индуктивност и съпротивление (виж фиг.2).
Напрежението на източника се разделя условно на две части - имайки предвид [2]
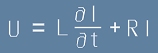 . [10]
. [10]
При включването на захранването, след време Т се установява равновесие, при което
общата извършена работа W се изразява с интеграла
 . [11]
. [11]
Заместваме [10] в [11]:
 , или
, или
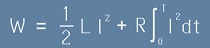 . [12]
. [12]
където L е индуктивността, R - съпротивлението на проводника, I - тока.
Второто събираемо в дясната страна на [12] e израз за топлинната енергия, разсейвана от съпротивлението R.
Първото е магнитната енергия в соленоида.
Ако в един момент изключим захранването, лявата страна на на [10] ще се окаже веднага нула.
Но енергията в полето и тока ще останат - те ще приемат нулева стойност след известно време,
защото в противен случай безкрайно бързата промяна в тока от I до 0 би предизвикало
безкрайно голям ток на самоиндукция.
Цялата енергия на веригата
от фиг.2 - натрупана чрез работата [12], веднага след изключване на захранването се намира в магнитното поле, тоест можем да смятаме, че
затихващият ток би извършил работа
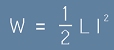 . [13]
. [13]
Да изразим тока чрез [6]:
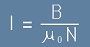 . [14]
. [14]
Да заместим [14] и [9] в [13]:
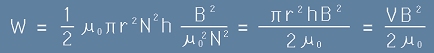 , [15]
, [15]
където с V е означен обема на полето:
 .
.
Посленият израз от [15] е енергията на магнитното поле.
От нея е удобно да се изрази отношението на енергията към обема, което представлява
Плътност на магнитната енергия
Тя се изразява с формулата:
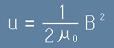 . [16]
. [16]
коментари
Радостин Желязков 03.04.2011
________________________________________________________________________________________
учебни статии по физика
 Соленоид
Соленоид
 Практически това е синоним на бобина или намотка. Представлява навит проводник
във форма на цилиндър с дължина h и диаметър 2r (виж фиг.1). Дължината h на идеалния соленоид трябва да е много по-голяма
от диаметъра. При тези условия можем да смятаме, че магнитното поле е съсредоточено изцяло във вътрешността
на намотката. Соленоида има собствена характеристика, наречена
Практически това е синоним на бобина или намотка. Представлява навит проводник
във форма на цилиндър с дължина h и диаметър 2r (виж фиг.1). Дължината h на идеалния соленоид трябва да е много по-голяма
от диаметъра. При тези условия можем да смятаме, че магнитното поле е съсредоточено изцяло във вътрешността
на намотката. Соленоида има собствена характеристика, наречена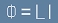 , [1]
, [1]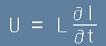 , [2]
, [2]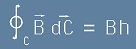 [3]
[3]  . [4]
. [4]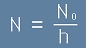 [5]
[5] . [6]
. [6]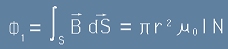 . [7]
. [7]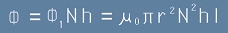 . [8]
. [8] , [9]
, [9] Схематично това се изобразява като последователно свързани индуктивност и съпротивление (виж фиг.2).
Напрежението на източника се разделя условно на две части - имайки предвид [2]
Схематично това се изобразява като последователно свързани индуктивност и съпротивление (виж фиг.2).
Напрежението на източника се разделя условно на две части - имайки предвид [2]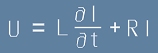 . [10]
. [10] . [11]
. [11] , или
, или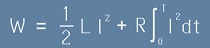 . [12]
. [12]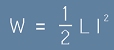 . [13]
. [13]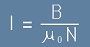 . [14]
. [14]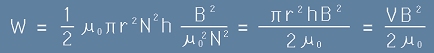 , [15]
, [15] .
.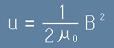 . [16]
. [16]