 Закон на Ом
Закон на Ом
Тук е представено обяснение на закона на Ом според класическата електромагнитна теория (Пол Друд, 1900).
Използувана е постановка близка до идеалния газ.
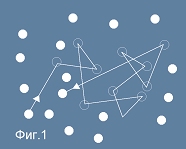 Електронен газ
Електронен газ
Класическото предположение на Лоренц-Друд е, че в металните тела,
електроните са свободни да се движат по целия обем,
както частиците от идеален газ - виж фиг.1. Изводът по-долу предполага, че когато няма електрично поле,
между два сблъсъка всеки електрон се движи праволинейно и равномерно. Електричното взаимодействие
между електроните не се отчита, освен като еластичен удар.
Когато към тялото е приложено електрично поле, към хаотичното движение се прибавя насочено движение с [постоянна] скорост, наричана още
Дрейфова скорост
По-долу тя е означена с Vd. Eлектричното поле означава, че на всеки електрон действува електрична сила:
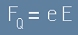 , [1]
, [1]
където E е интензитет на електричното поле, e - заряд на електрона,
FQ е електричната Кулонова сила. От тази сила възниква дрейфовата скорост.
Да означим средното време между два удара (тоест за свободен пробег) с T.
Съгласно формулата на Нютон F=dp/dt, отношението на дрейфовия импулс и това време, ще е равно на съпротивителната сила:
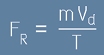 , [2]
, [2]
където FR е съпротивителната сила - еквивалент на предадения импулс за единица време,
m е масата на електрона, T е усреднено време между два удара, Vd е дрейфовата скорост на електрона.
При постоянен ток, горните две сили трябва да имат нулев сбор, тоест равни големини.
Да приравним десните страни на [1] и [2]. Това води до следния израз за Дрейфовата скорост:
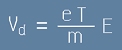 . [3]
. [3]
Нека n е броя на електроните в единица обем. В такъв случай, потока на броя частици е nVd
и тъй като всяка частица носи заряд e, потока на заряда ще бъде enVd.
"Поток на заряда" означава още
Плътност на електричния ток
Съгласно току-що казаното, тя е
 . [4]
. [4]
Да заместим дрейфовата скорост от [3] в [4]. За плътността на тока получаваме:
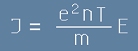 . [5]
. [5]
Нека означим с малка гръцка буква ро израза
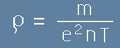 . [6]
. [6]
Очевидно неговите аргументи не са електрически и зависят от конкретния образец метал - n е числовата плътност на свободни електрони,
m и e са маса и заряд на електрона, T е времето за свободен пробег на един електрон. Този израз (ро) се нарича специфично съпротивление.
В такъв случай формулата от [5] ще придобие вид, близък до познатия от училище и обещан по-горе
 Закон на Ом
Закон на Ом
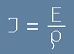 . [7]
. [7]
Да си представим метално тяло с дължина L и напречно сечение S - показано на Фиг.2.
Нека между лявата и дясната стена на тялото има електрическо напрежение.
Да умножим двете страни на [7] по сечението S:
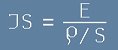 . [8]
. [8]
Сега да умножим числителя и знаменателя на дясната страна от [8] с дължината L на тялото:
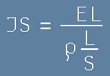 . [9]
. [9]
В лявата страна на [9] стои тока I=JS.
Когато полето E е еднородно, числителя от дясно на [9] съвпада с напрежението между лявата и дясната стена на тялото EL=U.
Да означим знаменателя в дясната страна на [9] с буква R и да го наречем електрично съпротивление на тялото:
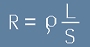 . [10]
. [10]
След тези уговорки, [9] се записва точно както е на стената на електротехникума:
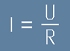 . [11]
. [11]
Радостин Желязков 02.06.2012
________________________________________________________________________________________
коментари
учебни статии по физика
 Закон на Ом
Закон на Ом
 Електронен газ
Електронен газ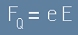 , [1]
, [1]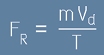 , [2]
, [2]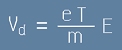 . [3]
. [3] . [4]
. [4] 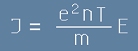 . [5]
. [5] 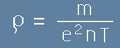 . [6]
. [6]  Закон на Ом
Закон на Ом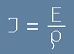 . [7]
. [7] 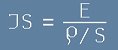 . [8]
. [8] 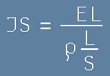 . [9]
. [9] 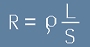 . [10]
. [10] 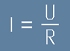 . [11]
. [11]