 Барометрична формула
Барометрична формула
Разпределението играе важна роля в термодинамиката и статистиката.
Тук е представен един прост пример за разпределение - на налягането във височина.
Трябва да сте запознати със статията идеален газ.
Добре е да погледнете учебния материал на Станчо Павлов за
неопределен интеграл.
В предната статия - "Идеален газ", равенство [9] разбрахме, че налягането е пропорционално на броя частици, масата на една частица и абсолютната температура на газа. Да напишем пак формулата за налягането:
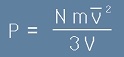 [1],
[1],
където N е броя на всички частици в газа, m е масата на една частица, V е обема а
v2 с черта над буквата е средния квадрат на скоростите на частиците.
Тъй като Nm/V е плътността на веществото (маса/обем),
стигаме до една важна закономерност - че
Налягането е пропорционално на плътността
 на идеалния газ:
От [1] се вижда, че Nm/V всъщност е плътността на газа (маса/обем) - да я означим с ро:
на идеалния газ:
От [1] се вижда, че Nm/V всъщност е плътността на газа (маса/обем) - да я означим с ро:
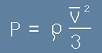 . [2]
. [2]
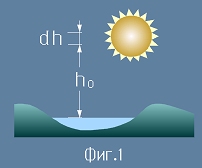
Всеки слой от атмосферата с дебелина dh има маса пропорционална на плътността на въздуха за тази височина. Но плътността се променя с височината. Безкрайно далеч от Земята, плътността е нула. Да изберем координатна ос h която започва от минус безкрайност,
насочена е към Земята и расте надолу, стигайки нула на морската повърхност.
Общата маса на стълб въздух над някаква хоризонтална площ A ще е :
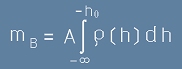 , [3]
, [3]
Интегралът от [3] е определен от минус безкрайност до минус h0.
Масата на този стълб въздух тежи върху площта A и създава налягане
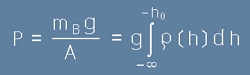 , [4]
, [4]
където mВ е масата на въздушния стълб, h0 е изследваната височина, ро е плътността на въздуха,
g е земното ускорение, A е площта върху която дейстува теглото на въздуха.
От [2] можем да изразим плътността на въздуха чрез налягането:
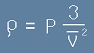 [5]
[5]
В статията "Идеален газ: видяхме, че средната кинетична енергия е пропорционална на температурата.
Ще приемем, че температурата е постоянна, тоест средният квадрат на скоростите не зависи от h. Да заместим [5] в [4]:
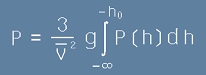 . [6]
. [6]
Как да намерим неизвестната функция P? Ако вземем производните на двете страни на [6], ще
получим обикновено диференциално уравнение.
Но няма нужда от това. От [6] виждаме, че функцията P(h) е равна на интеграл от себе си (умножен по константен израз).
Това може да се случи единствено, ако самата функция P(h) е експонента.
Е трябва още аргумента на експонентата да е умножен по израза пред интеграла.
Равенството [6] ще остане вярно ако го умножим по каква да е константа, което значи, че
функцията - решение на [6] може да е водена от константен множител P0:
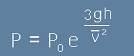 [61]
[61]
Константният множител P0 определено ще е налягане при височина нула,
тъй като експонента от нула е единица, а в ляво на [61] трябва да остане точното налягане на морското равнище.
Общата езикова конвенция е, че височината расте нагоре, затова нека да сменим посоката на координатната ос h, тоест да приемем, че безкрайна височина съответствува
на h клонящо към плюс безкрайност (значи да сменим знака на h от [61]):
 . [7]
. [7]
В тази формула - [7] - присъствува средния квадрат на скоростта.
Да си спомним, че той е пропорционален на абсолютната температура чрез
формула [11] от предната статия:
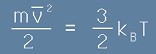 , тоест
, тоест
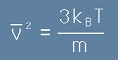 . [8]
. [8]
- където m е масата на една частица, kB е константата на Болцман, T е абсолютната температура.
Константата на Болцман е свързана с универсалната газова константа чрез формулата
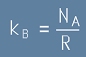 . [9]
. [9]
където R е универсалната газова константа, a с NA е означено
Числото на Авогадро
Според закона на Авогадро, при равни температури и налягане, порция еднакъв брой частици от различни газове заемат един и същ обем.
Да допуснем, че някакъв газ е съставен от еднакви частици.
Тогава масата на газа е равна на общия брой частици в него умножен по масата на една частица:
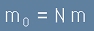 , [10]
, [10]
където m0 е общата маса на газа, m - маса на една частица, N - брой на всички частици.
Няма начин да се измери пряко масата m на една частица.
Вместо това се използува еталонен брой частици, наречен количество вещество или кратко мол.
По дефиниция, в един мол винаги има еднакъв брой частици, равен на
числото на Авогадро NA = 6.023*1023.
Масата на един мол от конкретно вещество (Моларната Маса) е:
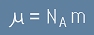 ,
тоест
,
тоест
 ,
[11]
,
[11]
където m е масата на една частица. Заместваме [11] в [9], [9] в [8] и [8] в [7], и така
стигнахме до споменатата в заглавието
Барометрична формула
Тя изразява гравитационно налягане на височина h за идеален газ с моларна маса мю, при абсолютна температура T и земно ускорение g, при стартово налягане за нулева височина P0:
 . [12]
. [12]
Въздухът, разбира се, не е точно идеален газ. Освен това, както е известно, той е съставен от поне три различни вида истински частици.
Но според законът на Далтон, всяка съставка в газа има независим дял в налягането,
така че формула [12] остава вярна при константна температура.
Практически пресмятанията за реалната атмосфера често се основават на тази формула.
коментари
Радостин Желязков 24.04.2011
________________________________________________________________________________________
учебни статии по физика
 Барометрична формула
Барометрична формула
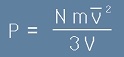 [1],
[1], на идеалния газ:
От [1] се вижда, че Nm/V всъщност е плътността на газа (маса/обем) - да я означим с ро:
на идеалния газ:
От [1] се вижда, че Nm/V всъщност е плътността на газа (маса/обем) - да я означим с ро: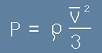 . [2]
. [2] , [3]
, [3]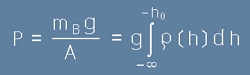 , [4]
, [4]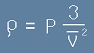 [5]
[5]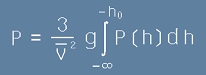 . [6]
. [6]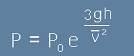 [61]
[61] . [7]
. [7]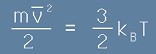 , тоест
, тоест
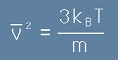 . [8]
. [8]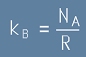 . [9]
. [9]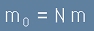 , [10]
, [10]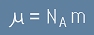 ,
тоест
,
тоест
 ,
[11]
,
[11] . [12]
. [12]