 Гаусово разпределение
Гаусово разпределение
Това е помощна статия, други текстове се обръщат към тази за справка.
Използувани са сведения от статии
Четна и нечетна функция,
Гаусови интеграли.
В предната статия (Гаусови интеграли) видяхме няколко решения на интеграли от експоненциална функция.
Тук обръщаме внимание на едно от тях -
Интеграл нула
Той е определен от нула до плюс безкрайност и изглежда така :
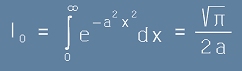 . [1]
. [1]
Нека заменим параметъра a с друг : b, такъв, че
 . [2]
. [2]
В такъв случай, интегралът [1] от по-горе ще се изрази чрез b като :
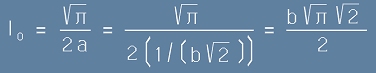 . [3]
. [3]
Ако границите на интегриране по-горе в [1] бяха по цялата числова ос, това щеше е
удвоената му стойност, тъй като подинтегралната функция е
четна.
Да заместим [2] и [3] в [1] и да го умножим по две:
 . [4]
. [4]
Ако b има такава стойност, че последният интеграл е точно равен на едно
(значи да разделим [4] на дясната му страна),
това се нарича нормиране и съответствува на известното
Нормално разпределение
 Условието за единична стойност на интеграла от [4] изглежда така:
Условието за единична стойност на интеграла от [4] изглежда така:
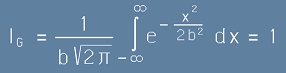 . [5]
. [5]
Подинтегралната функция
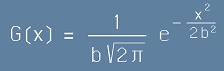 [6]
[6]
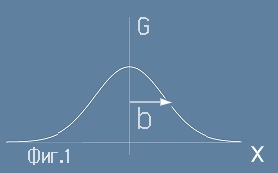
се нарича Гаусово разпределение, също наричано Нормално разпределение - виж Фиг.1
Параметърът b е мярка за ширината на камбанката и се нарича стандартно отклонение.
Случайно разпределени стойности около нулата, за които няма други условия обикновено се описват с тази формула.
коментари
Радостин Желязков 06.11.2011
________________________________________________________________________________________
учебни статии по физика
 Гаусово разпределение
Гаусово разпределение
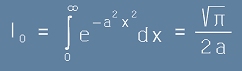 . [1]
. [1] . [2]
. [2]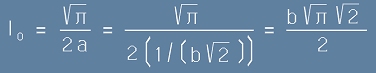 . [3]
. [3] . [4]
. [4] Условието за единична стойност на интеграла от [4] изглежда така:
Условието за единична стойност на интеграла от [4] изглежда така: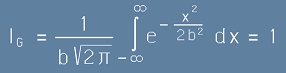 . [5]
. [5]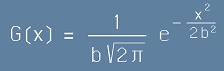 [6]
[6]