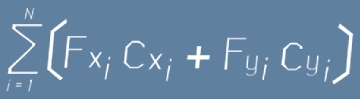Точка в полигон

Тук е описан начин за да определим дали една точка е вътре в даден контур.
Предназначен е за програмна технология, така, че някои теоретични формалности може да са пропуснати.

Текста по-долу може да се стори сложен и тудно разбираем за някого, но тъй като целта е програма, не е важно колко трудно я разбираме, нито дори колко е голяма и сложна. Важно е само да свърши работа и по възможност по-бързо. Реално получената програма не голяма, нито сложна. Публикувам този метод, защото за мен той се оказа решение. За цикъла са нужни само координатите на текущата отсечка x1,y1,x2,y2 - тоест тези, с които програмите за обслужване на контура боравят по принцип, както и параметрите Mx,My - координати на изследваната точка, означена по-долу с буква М.

Методът е основан на представата ни за електромагнитна индукция и закона на Фарадей.
В учебниците по електротехника можем да видим следната картинка, илюстрираща действието на трансформатора. Ако по намотката A тече променлив ток, той създава променливо магнитно поле чийто силови линии са затворени криви, както е показано тук:

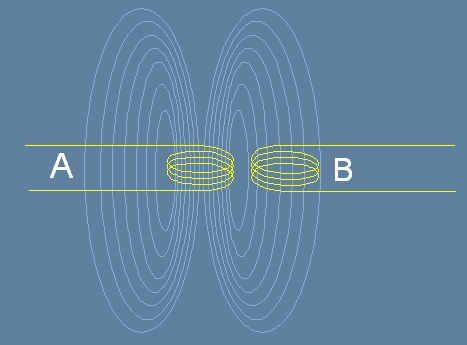
В намотката B, поставена в съседство, се индуцира електродвижещо напрежение /и ток, ако е натоварена/. Магнитното поле, пронизващо пръстена B, се явява средство за предаване на електричната енергия. За нашите цели е по-добре да разгледаме поле, състоящо се от една-единствена силова линия, вместо многото нарисувани по-горе. Да допуснем също, че това поле се променя с времето по един линеен и равномерен начин. Да означим с М точката, в която тази магнитната силова линия пробожда плоскостта на намотката B. Нека дори разгледаме само малък участък от силовата линия около точката M. Тази една магнитна линия поражда електрични сили - всъщност електростатично поле - което може да се изобрази със силови линии - концентрични окръжности в равнина перпендикулярна на магнитната силова линия.

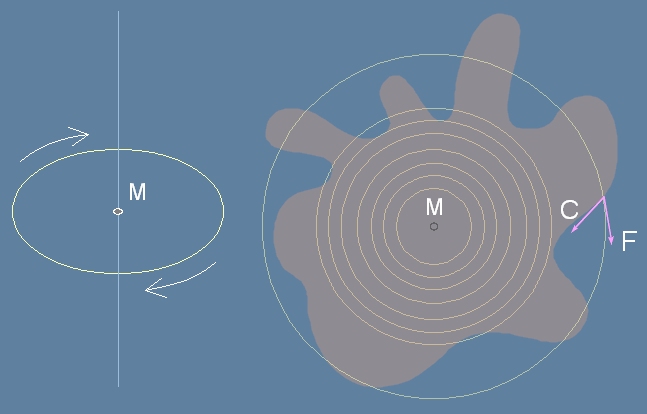
При въображаемия прост случай приемникът има форма на една от тези окръжности. Но в действителност явлението не изисква определена форма за намотката B, а само условието да е затворен контур и магнитната линия да го пробожда вътре. Във всяка точка от контура действува съставка на това концентрично поле, равна на проекцията на допирателния вектор F по силовата линия върху контура C. Или с други думи силата в един малък участък е равна на скаларното произведение от двата вектора F-силата на полето и C-направлението на контура.
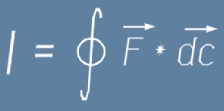
Общата индуцирана електродвижеща сила може да се оцени като интеграл от полето F, пресметнат по дължината на контура C.
Ако точката M е извън контура, този интеграл ще има нулева стойност.
В противен случай той е положителен или отрицателен, в зависимост от посоката на полето.
"Интеграл" може и да изглежда сложна дума понякога, но компютрите смятат интеграли лесно, тъй като за тях това са сборове.
Да означим с I въпросния интеграл и да го запишем:

Като сбор той изглежда по следния начин: Разделяме контура на N къси отсечки; За всяка от тях (с индекс i) пресмятаме векторите F,C и ги умножаваме скаларно. После сборуваме всички в едно число:



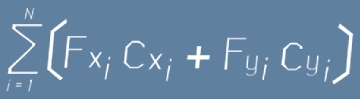
Коментар за грешката
Грешката расте с дължината на отсечката, за която допускаме, че полето F е постоянен вектор. Ако намалим дължината, грешката намалява, но се увеличава времето за пресмятане. За оценки, сързани с видмост по екрана, е достатъчна дължина от порядъка на няколко пиксела. Не се полъгвайте да броите дълги праволинейни участъци от контура като една отсечка. Това не е допустимо, тъй като полето F няма една и съща стойност по такава отсечка.

________________________________________________________________________________________
Радостин Желязков 19.10.2008

Други статии