Теорема на Питагор

Тук става дума за доказателство, което има доста стар произход.
Текстовете и формулите в тази страница са писани от мен, но рисунките, логиката и изводите са изобразени върху древни стени и предмети. Те се отнасят до Питагоровата теорема и Нютоновия бином.


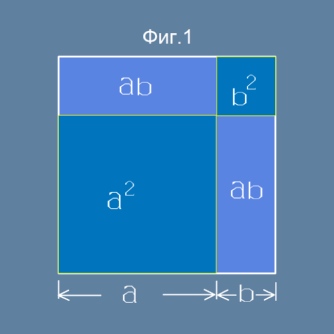
На фиг.1 е изобразен квадрат, чиято страна е разделена на две отсечки- означени с малки букви a и b. Нека означим с буква S площта на големия квадрат. Тази площ е съставена от два тъмни квадрата и два по-светли правоъгълника. Тъмните квадрати имат страни a и b. Всеки от двата по-светли правоъгълника има площ ab. Така площта на целия квадрат е сбор от всички тези, тоест:
[1]

Нека в същият този квадрат от горната фигура (фиг.1) разделим всяка от четирите страни пак на същите две части a и b и да свържем разделящите точки в друг квадрат, както е показано на следващата рисунка:

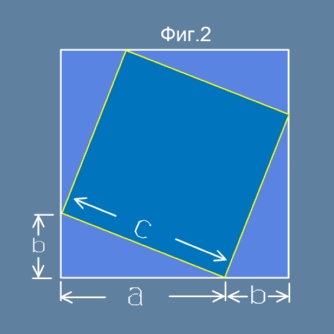
Общата площ е съставена от пет части - тъмния наклонен квадрат в средата и четири еднакви триъгълника, всеки от които има площ ab/2. Ако означим страната на тъмния квадрат с буквата c, то площта на целия квадрат е:
[2]
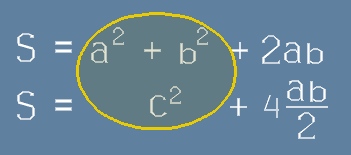
Нека запишем едно под друго двете равенства [1] и [2].
[3]
Почленно съпоставени, тези две равенства ясно показват, че дължината на страната на наклонения тъмен квадрат, която означихме по-горе с буква c спазва равенството:
[4]
и това е известната теорема на Питагор.


коментари

Радостин Желязков 09.07.2022
________________________________________________________________________________________

Начална страница
Други неподредени статии
учебни статии по физика