Най-късия път.
Късият път между И (играч) и Ц (цел).
Писал съм графични плоски машинки, свързани с географията на един от моите проекти.
Писал съм малки стрелящи игри (виж games_b.htm ), но не и стратегии. Въпреки това се осмелявам да публикувам този метод, който често сме обсъждали тук във фирмата когато говорим за игри. Без да имам претенции за най-добър, мисля че е разумен.
Целта на метода е да определи една стъпка на игровата единица, докато тя преследва своята цел. Забележете, че метода се опитва да заобиколи само един, най-близкия пречещ предмет. При следващата стъпка обстановката е друга и е нужно повторно изследване.
Игровите единици са човекоподобни и равнопоставени в общата карта. Значи каквито предмети вижда на картата човекът пред монитира, такива предмети виждат и компютърните играчи.
Правилното поведение не е абсолютният оптимум от гледна точка на алгоритмите, а най-близкото до очакваното от човешка гледна точка. Следователно са допустими и грешки в поведението на компютърните единици.
Този алгоритъм е опит за пресъздаване на живо поведение в подобна обстановка.
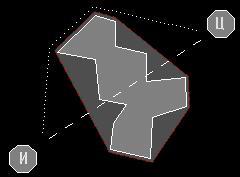
1. Определя се пречката. Това е предмет, който е най-близо до играча и пресича правата свързваща играча и целта.
2. Определят се двата пътя за заобикалянето на този предмет - левият и десният път.
3. Определя се по-късият път. (ако Л<=Д то К=Л иначе К=Д)
4. Стъпката е по така определения път.
===============================================
1. Как се определят пречките?
Предметите представляват затворени контури (един контур е поредица точки).
За всеки предмет правим изследването:
За всяка точка Т от контура се смята лицето на триъгълника И Т Ц. Ако всички получени лица имат еднакъв знак, предметът не е пречка. Ако предметът е пречка, запомняме в списък неговия идентификатор, както и отсечката, при която сме забелязали пресичането.
За всички предмети в списъка определяме разстоянието между точка И (играча) и записаната отсечка. Ако отсечката е АБ, То е равно на най-късото от трите разстояния ИА,ИБ,ИП, където П е петата на перпендикуляра от точка И към правата АБ.
След това изследване, можем да определим кой от предметите е най-близката пречка (Наречен в първа точка "пречката").
2. Как се определя левия път?
Определяме изпъкналата обвивка на пречката. Това е затворен контур, който задължително се явява и "пречка", макар и не най-близка.
- Определяме най-лявата точка на обвивката (тази, за която косинуса е най-малък). После повтаряме същото, ако все още обвивката е "пречка".
===============================================
Приложения:
1. Лице на триъгълник: RPlace
2. Разстояние от точката И до петата на перпендикуляра към правата АБ: PointToLine
Function RPlace(x1,y1,x2,y2,x3,y3:real):real;
begin RPlace:=(x1*(y2-y3)+x2*(y3-y1)+x3*(y1-y2));end;
Function PointToLine(xp,yp,x1,y1,x2,y2:longint):longint;
var
l,l2,l3,lq1,lq2,lq3:real;Ostro:boolean;
begin
lq1:=Sqr(1.0*xp-x1)+Sqr(1.0*yp-y1);
lq2:=Sqr(1.0*xp-x2)+Sqr(1.0*yp-y2);
lq3:=Sqr(1.0*x2-x1)+Sqr(1.0*y2-y1);
l3:=round(Sqrt(lq3));
Ostro:=(l3<>0) and (lq3+lq2>lq1) and (lq3+lq1>lq2);
if Ostro then l:=abs(RPlace(x1,y1,x2,y2,xp,yp))/ l3
else
begin
l2:=min(lq1,lq2);
l:=Sqrt(l2);
end;
PointToLine:=round(l);
end;
3. Как се определя изпъкналата обвивка на обект?
Имам решение на тази задача, но мисля, че изпъкналата обвивка би могла да бъде свойство на самия обект, това е по-евтино решение, поне за мен, тъй като определянето на изпъкнала обвивка е програма, която би заела стотина линии и не е подходяща за публикуване. Освен това еднократното определяне на обвивката е по удобно в момента, когато се формира самия контур на предмета, а не по време на изследването, Така че този въпрос ми с вижда леко в страни от темата.
РЖ 22.07.2004
начална страница
други статии
