 Уравнения на Хамилтон
Уравнения на Хамилтон
Хамилтон е написал тези уравнение 45 години след Лагранж.
Той се е възхищавал от Лагранжевия подход и го е определил като "научна поема".
Трябва да сте запознати с Функция на Лагранж.
Формализъм
В уравнението на Ойлер-Лагранж
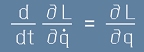 [1]
[1]
с L е означена Лагранжевата функция
 , [2]
, [2]
с q са означени обобщените координати, а техните производни по времето са означни с точка върху буквата
(виж обобщени координати и скорости от статията за Лагранж).
Лагранжевата функция е L=T-U , където T и U са кинетична и потенциална енергия.
Уравнението на Ойлер-Лагранж [1] , както и Хамилтоновите уравнение по-долу са пряко следствие от
Нютоновата механика.
Но те не съдържат явни зависимости от маса и декартови координати.
Това са целенасочени обобщения, което ги прави удобни за прилагане в някои случаи.
Хамилтон въвежда понятието
Обобщен импулс
който представлява производна на Лагранжевата функция по обобщената скорост:
 . [3]
. [3]
Тази дефиниция е подбрана така, че да е напълно съвместима с Нютоновия импулс в декартови координати.
Ето една илюстрация: Тъй като потенциалната енергия U не зависи от обобщените скорости,
 . [4]
. [4]
При движение на едно тяло с маса m и скорост v, в декартови координати получаваме
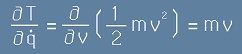 . [5]
. [5]
* * *
Заедно с обобщения импулс Хамилтон въвежда и наречената по-късно
Функция на Хамилтон
 [1h]
[1h]
- като функция на обобщени координати, обобщени импулси и време.
Тази функция се нарича понякога Хамилтониан.
Тя произвежда две уравнения, които описват
движението на механичната система:
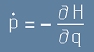 [2h]
[2h]
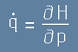 [3h]
[3h]
Те се наричат Уравнения на Хамилтон или понякога канонични уравнения.
Постановката на Хамилтон [1h], [2h], [3h] често се възприема като базова, тоест отправна точка за разсъждения.
По-долу обаче е показано как тя следва от Лагранжевото уравнение [1].
Хамилтоновата функция представлява образ на Лагранжиана, получен чрез
Трансформация на Лежандър
Лежандър е френски математик - асоцииран член на Парижката академия,
високо почитан от Лагранж и негов съвременник, от времето на Наполеон.
Лежандровата трансформация построява от една реална, друга реална функция.
Следва описание на тази процедура, в контекста на нашата цел:
Нека f е реална функция на две променливи
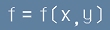 . [Le1]
. [Le1]
Да означим частните производни по двете променливи с буквите u и v:
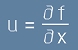 и
и
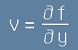 . [Le2]
. [Le2]
Диференциала (безкрайно малката промяна) на такава функция изглежда така:
 . [Le3]
. [Le3]
Образа (новата функция) се дефинира като друга функция
 , [Le4]
, [Le4]
в която, както виждаме едниния аргумент е заменен с производната на f по x.
и (внимание!) новата функция има вид:
 . [Le5]
. [Le5]
Диференциала на новата функция би бил
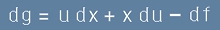 . [Le6]
. [Le6]
тоест, имайки предвид [Le3]
 ,
,
и остава
 . [Le7]
. [Le7]
Сега, ако запишем по аналогия с [Le2] и [Le3] диференциала на g :
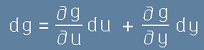 , [Le8]
, [Le8]
съпоставката на [Le8] и [Le7] води до
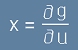 и
и
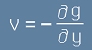 . [Le9]
. [Le9]
Да пристъпим към нашето преобразуване, тръгвайки от функцията
 . [Le10]
. [Le10]
ще построим нейн образ
 . [Le11]
. [Le11]
По аналогия с [Le5], той би трябвало да има вид
 . [Le12]
. [Le12]
Да заместим в [Le12] дефиницията на обобщения импулс от [3]:
 . [Le13]
. [Le13]
Да пресметнем и диференциала на [Le13]:
 . [Le14]
. [Le14]
В третия член на [Le14] виждаме като множител [3], тоест
 .
.
така диференциала на H остава
 . [Le15]
. [Le15]
Съгласно уравнението на Ойлер-Лагранж от [1] и [3] можем да изразим
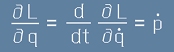 , [Le16]
, [Le16]
а ако заместим това в [Le15], виждаме, че
 . [Le17]
. [Le17]
Но на общо основание, според [Le11] трябва
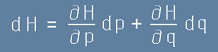 . [Le18]
. [Le18]
За да бъдат верни [Le18] и [Le17] е нужно
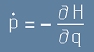 и
и
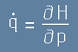 [Le19] .
[Le19] .
Последните две равенства съвпадат с [2h] и [3h] - каноничните Хамилтонови уравнения.
* * *
Обобщените координати и обобщените импулси съставят пространство, наричано понякога
Фазово пространство
Има пример как фазовото пространство може да е образно:
Да си представим пружина с линейно нарастваща еластична сила
F=-kx ,
в края на която има маса m.
Потенциалната енергия, при отклонение x от равновесното положение е
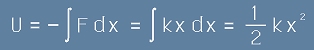 , а кинетичната
, а кинетичната
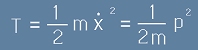 .
.
Пълната енергия можем да запишем като
 . [6]
. [6]
Да въведем фазова координата 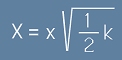 , фазов импулс
, фазов импулс 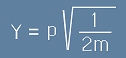 и да означим
и да означим
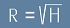 . [7]
. [7]
В такъв случай [6] е еквивалент на уравнвние на окръжност:
 , [8]
, [8]
тоест отговарящо на идеята за хармоничен осцилатор, какъвто е описан в статията
"Трептящ кръг".
Функцията на Хамилтон най-просто се тълкува като сбор от кинетична и потенциална енергия: H=T+U,
тоест като
Пълна енергия
на механичната система.
По-горе в [6] има ясен израз на такава енергия - за хармоничния осцилатор
и от нея се вижда например, че двете производни са
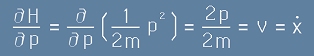 , [9]
, [9]
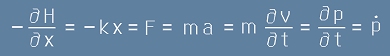 . [10]
. [10]
което съвпада с каноничните уравнения [2h] и [3h] от по-горе.
коментари
Радостин Желязков 20.04.2011
________________________________________________________________________________________
учебни статии по физика
 Уравнения на Хамилтон
Уравнения на Хамилтон
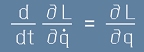 [1]
[1] , [2]
, [2] . [3]
. [3] . [4]
. [4]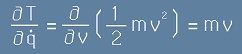 . [5]
. [5] [1h]
[1h]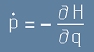 [2h]
[2h]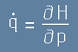 [3h]
[3h]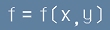 . [Le1]
. [Le1]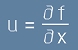 и
и
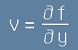 . [Le2]
. [Le2] . [Le3]
. [Le3] , [Le4]
, [Le4] . [Le5]
. [Le5]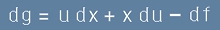 . [Le6]
. [Le6] ,
, . [Le7]
. [Le7]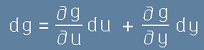 , [Le8]
, [Le8]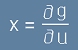 и
и
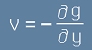 . [Le9]
. [Le9] . [Le10]
. [Le10] . [Le11]
. [Le11] . [Le12]
. [Le12] . [Le13]
. [Le13] . [Le14]
. [Le14] .
.  . [Le15]
. [Le15]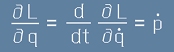 , [Le16]
, [Le16] . [Le17]
. [Le17]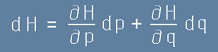 . [Le18]
. [Le18]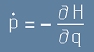 и
и
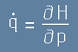 [Le19] .
[Le19] .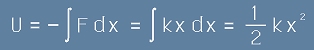 , а кинетичната
, а кинетичната
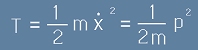 .
. . [6]
. [6]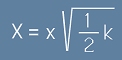 , фазов импулс
, фазов импулс 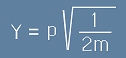 и да означим
и да означим
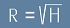 . [7]
. [7] , [8]
, [8]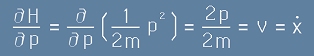 , [9]
, [9]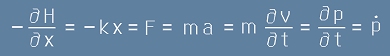 . [10]
. [10]