 Антена
Антена
Това е част от електротехниката.
Изведен е израз за излъчването на дипола на Херц-най-простия модел на антена.
Използувани са сведения от статиите
Формула на Лармор,
Променлив ток.

Дипол на Херц
Това е прав тънък проводник, чиято дължина е малка в сравнение с дължина на вълната - виж Фиг.1.
Нека дължината на проводника L е по направление z.
По определение електричният ток е поток на количеството електричен заряд за единица време.
Чрез формула това изглежда като производна:
 . [1]
. [1]
Движението на заряд q, може да се представи като сложна
функция q=q(z(t)), така, че горната формула ще се преобрази в
 , но тъй като
, но тъй като
 , [2]
, [2]
където v е скоростта на зарядите,
токът се изразява като
 , [3]
, [3]
Променливите токове предполагат променяща се скорост и плътност на зарядите в проводника.
Горния израз [3] е предназначен да представи тока в малка област dz по дължината на антената (Фиг.1).
Всеки заряд, чиято скорост се променя, излъчва електромагнитни вълни. По-долу ще оценим
Полето
създавано от целия дипол на Херц. Напречна съставка на електричното поле, създавано от точков заряд
ни е известна от равенство [11] от статията Формулата на Лармор:
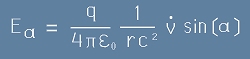 . [11L]
. [11L]
Зарядът в участъка dz - затова по-горе е казано, че проводникът трябва да е тънък -
може да се разглежда като точков. Да го означим с dq и да означим с dE полето, възникващо от него.
Но как ускорението на този точков заряд е свързано с тока?
Променливият ток
(виж равенство [1] от едноименната статия)
най-често се разглежда като
решение на уравнението за хармоничен осцилатор
и като комплексна функция от времето има вид:
 . [4]
. [4]
Предвидливостта изисква в горното уравнение да изберем минусов знак на степенния показател.
Но за момента ще го оставим с плюс, за да избегнем минусите в следващите
експоненти. Малко по-долу ще си го върнем на минус.
Пропорцията между тока и скоростта, изразена в [3], както и съпоставката с [4] води лесно до
формула за скоростта на зарядите като функция от времето:
 . [5]
. [5]
От [5] се вижда и ускорението на заряда:
 . [6]
. [6]
След [6] и казаното по-горе можем да напишем излъчването на Лармор за участъка dz - заместваме в [11L]:
 . [7]
. [7]
Целият дипол - с дължина L - ще има сборно поле
 , [8]
, [8]
Сега вече от [3] се вижда, че подинтегралната функция е всъщност тока.
Съгласно уговорката най-горе, дължината на дипола L трябва да е доста по-малка от дължината на вълната,
така, че по половината рамо няма място за цяла синусоида, а се нанася само малък участък от нея.
В този случай тока е с една и съща големина по цялата дължина на дипола.
Интегралът от [8] е равен на IL и след заместване от [4], полето, създавано от дипола е:
 . [9]
. [9]
Енергиен поток
Както знаем, енергийният поток на електромагнитното поле е вектора на Пойнтинг
(виж [4] от статията Формула на Лармор).
 . [4L]
. [4L]
Да заместим [9] в горното равенство. (сега е момента да върнем минусовия знак, зает по-горе).
Ще получим вектора на енергийния поток в направление алфа спрямо полярната ос на дипола:
 . [10]
. [10]
Съгласно формулата на Ойлер,
 . [11]
. [11]
Реалната част е
 , [12]
, [12]
 а реалната част на експонентата от [10] е
а реалната част на експонентата от [10] е
 . [13]
. [13]
Тъй като оценката за енергиен поток е усреднена във времето,
вместо да ползуваме квадрата на косинуса от [13],
можем да го заменим със средната стойност на cos2 във времето, която е 1/2.
За излъчваната енергия, в направление алфа, вместо [10], остава израза:
 . [14]
. [14]
Излъчването е осево-симетрично, по полярната ос на дипола е нулево, а най-силно е
по екватора. Диаграмата на насоченост е с тороидална форма (Фиг.2).
Интеграл
 Да разгледаме пръстеновидния участък от сфера, центрирана около дипола,
Да разгледаме пръстеновидния участък от сфера, центрирана около дипола,
изобразен на Фиг.3. Той има повърхност
 [15]
[15]
и потока на енергията от [14] е един и същ по този пръстен.
Общата излъчавана енергия ще е интеграл по цялата сфера:
 , [16]
, [16]
или по-кратко:
 . [17]
. [17]
Последният интеграл е решен в [19] от статията Формулата на Лармор и е равен на 4/3, така, че
общата енергия, която излъчва дипола на Херц е:
 . [18]
. [18]
коментари
Радостин Желязков 19.08.2011
________________________________________________________________________________________
учебни статии по физика
 Антена
Антена

 . [1]
. [1] , но тъй като
, но тъй като
 , [2]
, [2] , [3]
, [3]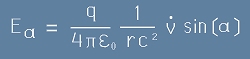 . [11L]
. [11L] . [4]
. [4] . [5]
. [5] . [6]
. [6] . [7]
. [7] , [8]
, [8] . [9]
. [9] . [4L]
. [4L] . [10]
. [10] . [11]
. [11] , [12]
, [12] а реалната част на експонентата от [10] е
а реалната част на експонентата от [10] е
 . [13]
. [13] . [14]
. [14] Да разгледаме пръстеновидния участък от сфера, центрирана около дипола,
Да разгледаме пръстеновидния участък от сфера, центрирана около дипола, [15]
[15] , [16]
, [16] . [17]
. [17] . [18]
. [18]