 Формула на Лармор
Формула на Лармор
Това е част от класическата електродинамика.
Изведен е по сравнително прост начин израза на Лармор за излъчване от ускорена частица.
Лармор е живял заедно с Ръдърфорд и Дж. Дж. Томсън.
Изложението по-долу е съвременно и вероятно не е същото, каквото е било направено от Лармор.
Използувани са предни статии
Вектор на Пойнтинг,
Плоска вълна,
Електромагнитни вълни.
Разсъжденията по-долу са при ясни посоки на векторите, затова ще използуваме
означения само за дължините им.
Полето, създавано от електричен заряд според Закона на Кулон е
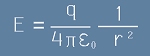 . [1]
. [1]
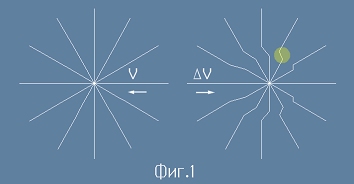
Силовите линии
при неподвижен заряд са радиално-симетрични прави.
Ако заряда-източник се движи с постоянна скорост, полето изглежда по
същия начин - тези два случая са неразличими - такова поле е изобразено в лявата страна на Фиг.1.
Но ако заряда се движи с ускорение , линиите вече не са прави, а по тях пробягва
деформация - вълнов процес, който се разпространява със скоростта на светлината -
виж дясната рисунка от Фиг.1 - предполага се, че скоростта e отдясно наляво, a ускорението - обратно.
Вълновите процеси пренасят енергия и в този случай източника на енергията е самият заряд,
който се движи с променлива скорост. От по-рано имаме оценка за потока енергия, пренасяна
от електромагнитните вълни - виж равенство [1] от статията "Вектор на Пойнтинг".
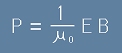 . [2]
. [2]
Освен това, от равенство [14] от статията "Плоска вълна" знаем какво е съотношението
между електричния и магнитния вектор.
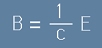 . [3]
. [3]
Ако погледнем връзката между скоростта на светлината c и двете константи мю и епсилон -
магнитната и диелектричната проницаемост -
изразена във формула [11] от статията Електромагнитни вълни, можем да заместим [3] в [2]
и да получим следния кратък израз за вектора на Пойнтинг:
 . [4]
. [4]
 Сега да се съсредоточим върху изкривяването на силовата линия - жълтото петно на Фиг.1, което
е изобразено в
Сега да се съсредоточим върху изкривяването на силовата линия - жълтото петно на Фиг.1, което
е изобразено в
Едър план
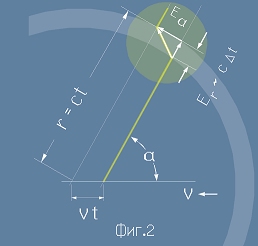
на Фиг.2. Силовия вектор E може да се представи като сбор от надлъжна и напречна съставка.
Нека зарядът се движи равнозакъснително, намалявайки скоростта си от v до нула за време
 .
Отрицателното ускорение ще предизвика вълнов импулс, който достига разстояние
.
Отрицателното ускорение ще предизвика вълнов импулс, който достига разстояние
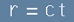 след време t.
след време t.
Ще разгледаме поотделно двете съставки.
Вълната се разпространява с постоянна скорост. Надлъжната (радиалната) съставка е:
 . [5]
. [5]
/ Вълничката "~" в [5] и по-долу замества фразата "е пропорционално на"./
Напречната съставка  ще оценим геометрично от Фиг.2.
ще оценим геометрично от Фиг.2.
Извън черупката на вълновия импулс, силовата линия "не знае", че е настъпила промяна. Тя е там,
където щеще да е, ако частицата продължава да се движи равномерно праволинейно със скорост v,
тоест на разстояние vt.
 . [6]
. [6]
От горните две пропорции следва, че
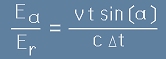 , или
, или
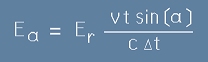 . [7]
. [7]
Електромагнитните вълни са напречни. Надлъжната съставка е статичното Кулоново поле от [1].
След заместване на Er от [1] в [7], получаваме
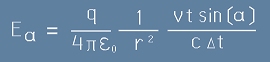 . [8]
. [8]
Да заместим в горната формула изразите за радиуса на вълновата сфера
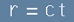 и ускорението
и ускорението
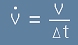 . [9] :
. [9] :
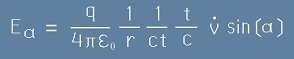 . [10]
. [10]
или по-кратко напречната (тангенциалната) съставка на полето е
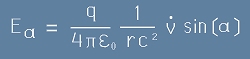 . [11]
. [11]
Да заместим този резултат в израза за
Поток на енергията
чрез вектора на Пойнтинг от по-горе в равенство [4].
Ще получим израз за излъчваната енергия по ъгъл алфа спрямо посоката на ускорението и разстояние r:
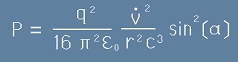 . [12]
. [12]
В тази формула [12] има симетрия спрямо екваториалната плоскост. Излъчваната енергия е една и съща в двете посоки - напред и назад.
Освен това, тази формула очевидно има осева симетрия по направление на ускорението.
За да получим
 Интеграл
Интеграл
на потока през цялата сфера, можем да разчитаме на тази симетрия.
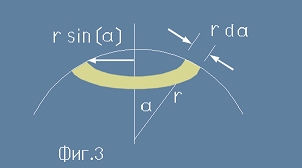
Фиг. 3 показва един пръстен (жълт цвят) - част от повърхността на сфера около нашия заряд. По този пръстен векторът от [12] има постоянна големина.
Размерите на пръстена са лесни за съобразяване. Повърхността му е
 . [13]
. [13]
А търсеното излъчване, като енергия за единица време, представлява интеграла
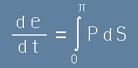 . [14]
. [14]
Да заместим [12] и [13] в [14]:
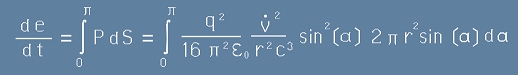 . [15]
. [15]
Малко опростяваме:
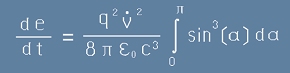 . [16]
. [16]
По всичко изглежда, че трябва да решим интеграла:
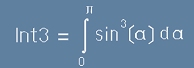 . [17] - това не е трудно,
. [17] - това не е трудно,
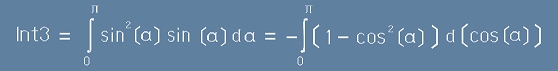 , [18] и накрая
, [18] и накрая
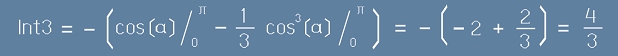 . [19]
. [19]
Заместваме този резултат в [16] и получаваме
Формулата на Лармор
която показва колко енергия излъчва за единица време заряд q, движещ се с ускорение:
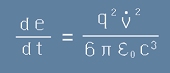 . [20]
. [20]
коментари
Радостин Желязков 20.06.2011
________________________________________________________________________________________
учебни статии по физика
 Формула на Лармор
Формула на Лармор

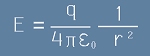 . [1]
. [1]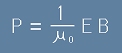 . [2]
. [2]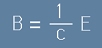 . [3]
. [3] . [4]
. [4] Сега да се съсредоточим върху изкривяването на силовата линия - жълтото петно на Фиг.1, което
е изобразено в
Сега да се съсредоточим върху изкривяването на силовата линия - жълтото петно на Фиг.1, което
е изобразено в .
Отрицателното ускорение ще предизвика вълнов импулс, който достига разстояние
.
Отрицателното ускорение ще предизвика вълнов импулс, който достига разстояние
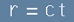 след време t.
след време t. . [5]
. [5] ще оценим геометрично от Фиг.2.
ще оценим геометрично от Фиг.2. . [6]
. [6]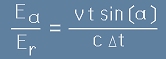 , или
, или
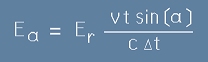 . [7]
. [7]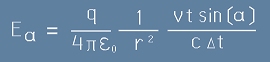 . [8]
. [8]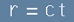 и ускорението
и ускорението
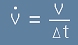 . [9] :
. [9] :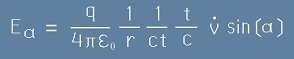 . [10]
. [10]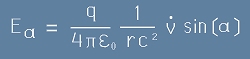 . [11]
. [11]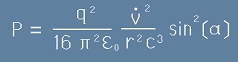 . [12]
. [12] Интеграл
Интеграл . [13]
. [13]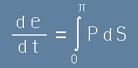 . [14]
. [14]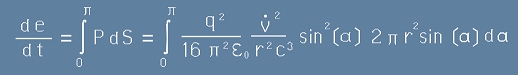 . [15]
. [15]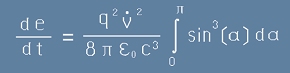 . [16]
. [16]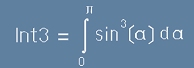 . [17] - това не е трудно,
. [17] - това не е трудно, 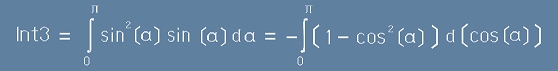 , [18] и накрая
, [18] и накрая 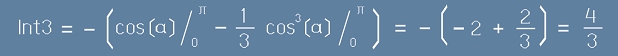 . [19]
. [19] 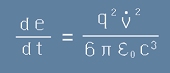 . [20]
. [20]