 Вектор на Пойнтинг
Вектор на Пойнтинг
Това е част от класическата електромагнитната теория.
Трябва да сте запознати с:
Набла операции,
Уравненията на Максуел,
Електромагнитни вълни,
Плоска вълна,
Кондензатор,
Соленоид,
Уравнение на Поасон.
Поток на енергията
Електромагнитните вълни пренасят енергия.
Потока на електромагнитната енергия е вектор, чиято посока съвпада с посоката на разпространение
на вълната а големината му съответствува на плътност на потока енергия.
Дефиницията за този вектор е
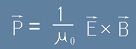 .[1]
.[1]
Той има размерност ват/квадратен метър - W/m2
и се нарича Вектор на Пойнтинг, или още Вектор на Умов.
По-долу ще покажем как именно дефинирания в [1] вектор представлява енергия.
Да оценим енергийния поток по геометричен начин. Да си представим затворена повърхност S,
и да означим с V обема вътре в нея.
Лесно е да съобразим ,че колкото е потока на енергията през повърхността S навън,
с толкова ще намалее количеството обща енергия U вътре в обема V :
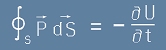 .[1.1]
.[1.1]
Съгласно теоремата за дивергенцията (виж статията Поасон, потока на енергия спазва равенството
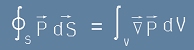 .[2]
.[2]
Да заместим [1] в дясната част на [2]:
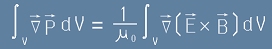 .[3]
.[3]
Да погледнем "Тъждество 2" от статията "Набла операции". Подинтегралната функция в дясно на [3] е
 .[4]
.[4]
Но в дясно на [4] двата изрази в скобите са известни от
трето и четвърто уравнение на Максуел, така, че
 .[5]
.[5]
Заместваме [5] в дясно на [3], после лявата страна на [3] с равната й от [2] и съответно [1.1]:
 .[5]
.[5]
Да пресметнем специално първия член отдясно на [5], тоест съставката
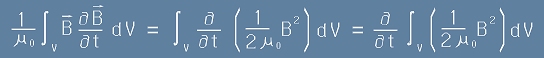 .[6]
.[6]
Както и втория член отдясно на [5], тоест съставката
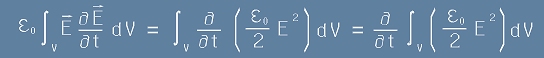 .[7]
.[7]
Електрична и магнитна плътност
Да въведем означение
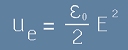 .[8]
.[8]
Ако погледнем равенство [7] от статията "Кондензатор", ще видим че това е плътност на електричната енергия.
Електричната енергия на полето ще бъде интеграл на [8] по обема:
 .[8.1]
.[8.1]
Да означим също и
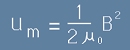 .[9]
.[9]
Ако погледнем равенство [16] от статията "Соленоид", ще видим че това е плътност на магнитната енергия.
Магнитната енергия на полето ще бъде интеграл на [9] по обема:
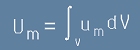 .[9.1]
.[9.1]
Заместването на [8] и [9] в [6] и [7], после в [5] води до еквивалентно на [5] равенство:
 .[10]
.[10]
Което казва, че във вакуум (където няма ток на проводимост и последния член в дясно на [10] ще е нула),
сбора на електричната и магнитната се равнява на пълната енергия на полето.
Това е съгласие с твърдението, че векторът от [1] действително е поток на енергия.
Теорема на Пойнтинг
Да означим с u сбора u = ue + um - обща плътност на енергията в полето.
От написаното по-горе разбира се следва и равенството
 .[11]
.[11]
наречено още Теорема на Пойнтинг.
Доказателството е почти видимо от горе - направете го сами.
коментари
Радостин Желязков 05.04.2011
________________________________________________________________________________________
учебни статии по физика
 Вектор на Пойнтинг
Вектор на Пойнтинг
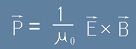 .[1]
.[1]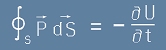 .[1.1]
.[1.1]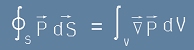 .[2]
.[2]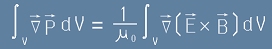 .[3]
.[3] .[4]
.[4] .[5]
.[5] .[5]
.[5]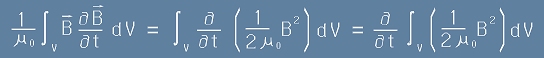 .[6]
.[6]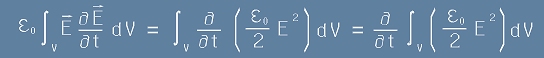 .[7]
.[7]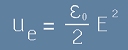 .[8]
.[8] .[8.1]
.[8.1]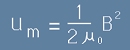 .[9]
.[9]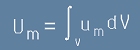 .[9.1]
.[9.1] .[10]
.[10] .[11]
.[11]