 Капацитет
Капацитет
Това е част от класическата електромагнитната теория.
Трябва да сте запознати с:
Набла операции,
Уравненията на Максуел,
Уравнение на Поасон.
Кондензаторът по-долу е "идеален" - модел, чийто цел е да "затвори" полето в удобен за тълкуване
геометричен примитив. Технологичните кондензатори обикновено се отклоняват от него.
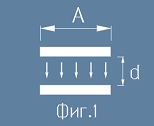 Кондензатор
Кондензатор
Това са две успоредни проводящи плочи във вакуум, на малко разстояние една от друга и с голяма повърхност (фиг.1).
Ще смятаме, че цялото поле е съсредоточено в пространството между тях.
Да пренесем единица заряд от едната плоча до другата срещу силите на електричното поле.
При преодоляването на полето ще извършим работа W=qU.
(където W е работата, q е заряда, U е напрежението между плочите).
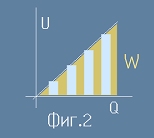
Ако пренесем втори заряд, насрещната сила ще е по-голяма,
защото току-що пренесения заряд се прибавя към източника на полето
и напрежението расте пропорционално на натрупания заряд (фиг.2).
Всеки следващ ще се движи все по-трудно - ще изисква повече работа от предния.
Интегралът на извършената работа (жълтия триъгълник на фиг.2) ще е
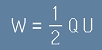 .[1]
.[1]
където W е извършената работа, Q е общото количество заряд, U е крайното напрежение.
Капацитет
Капацитетът се дефинира като количество заряд, което повишава напрежението с един волт Q/U.
Кондензаторът има две плочи. Да си представим, че едната от тях е обвита от затворена повърхност S - виж фиг.3.
Да напишем теоремата за дивергенцията (виж
равенство [2] от Уравнение на Поасон)
на електрично поле
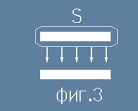 (в следващите три равенства площта е означена с S) :
(в следващите три равенства площта е означена с S) :
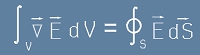 [c1]
[c1]
В лявата страна на [c1], подинтегралната функция съвпада с лявата страна на първото
уравнение на Максуел,
така, че
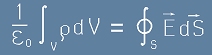 [c2]
[c2]
Интеграла в лявата страна на [c2] е всъщност електричния заряд. Ако този заряд е разположен по повърхността
на разглежданата област, може да се представи като повърхностна плътност умножена по площта:
 ,[c3]
,[c3]
където с малка гръцка буква сигма е означена повърхностната плътност на заряда.
От [c3] пряко се вижда, че
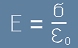 .[c4]
.[c4]
С което вече можем да пресметнем отношението, както е казано в дефиницията за капацитет -
при площ A за едната плоча и междина d:
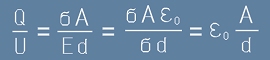 [c5].
[c5].
Горното се отнася за "обвитата" плоча от кондензатора. Всяка от двете плочи държи половината
заряд (и според [c5] - половината капацитет) на кондензатора.
Можем да "махнем" обвивката на плочата - [c5] ще е капацитет на целия кондензатор.
Напрежението U и зарядът Q в кондензатора винаги спазват равенството
Q = CU
, [2]
където C е капацитета. Така, че
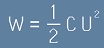 . [3]
. [3]
Капацитетът на кондензатора се представя с формула (виж по-горе [c5])
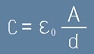 , [4]
, [4]
където епсилон е диелектричната проницаемост на вакуума,
A е площта на кондензаторните плочи, а d е разстоянието между тях - виж фиг.1.
Напрежението U съответствува на електрично поле E по формулата
U = Ed
. [5]
За работата от [3] [4] и [5] се получава 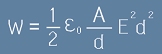 , и по-точно
, и по-точно
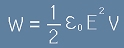 , [6]
, [6]
където с
V = Ad
е означен обема между двете плочи, в който е съсредоточено полето.
Разбира се, тази работа е равна на натрупаната
Енергия на електричното поле,
за което по-горе казахме,
че е изцяло съсредоточено между двете повърхности на кондензатора.
В изразът [6] обемът на това пространство е множител, така, че ако го премахнем,
получаваме енергия в единица обем, тоест
Плътност на енергията на електричното поле
Както виждаме от [6], плътността на енергията е :
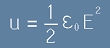 . [7]
. [7]
коментари
Радостин Желязков 02.04.2011
________________________________________________________________________________________
учебни статии по физика
 Капацитет
Капацитет
 Кондензатор
Кондензатор
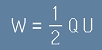 .[1]
.[1] (в следващите три равенства площта е означена с S) :
(в следващите три равенства площта е означена с S) :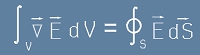 [c1]
[c1]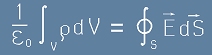 [c2]
[c2] ,[c3]
,[c3]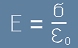 .[c4]
.[c4]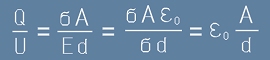 [c5].
[c5].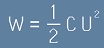 . [3]
. [3]
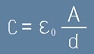 , [4]
, [4]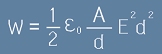 , и по-точно
, и по-точно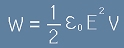 , [6]
, [6]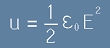 . [7]
. [7]