 Променлив ток
Променлив ток
Това е част от електротехниката.
Тук са използувани знания от статиите
Трептящ кръг,
Кондензатор.
Соленоид.
Колебателните процеси се уподобяват на математически модел - примитив, наречен хармоничен осцилатор и вече коментиран в статията "Трептящ кръг".
Най-общо, решението на уравнението за хармоничния осцилатор изглежда като
Kомплексна функция
от времето:
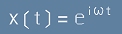 [1]
[1]
Но в електричните схеми, предметът който се движи, е електричния заряд. Ако в лявата страна на
горното уравнение трябва да има електричен заряд, то вдясно се полага пропорционален множител, чиято
размерност е също заряд. Тоест уравнението за движение се превежда към функция q(t) като
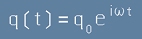 , [2]
, [2]
където q е заряда, а вдясно q0 е множител на пропорционалност.
Във всяка електрична верига присъствуват капацитети, по явен или неявен начин. Да разгледаме
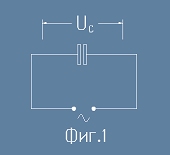 Кондензаторът
Кондензаторът
от фиг.1. Напрежението в краищата на всеки кондензатор, в кой да е момент спазва правилото:
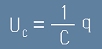 , [3]
, [3]
където C е капацитета на кондензатора, q е заряда, а Uc е напрежението между двата извода.
Изразено като функция на времето - [2] в [3], то изглежда като комплексна функция:
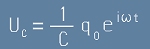 . [4]
. [4]
Токът се определя като първа производна на заряда по времето:
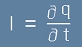 , [5]
, [5]
или като заместим [2] :
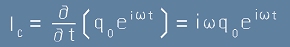 . [6]
. [6]
Токът през кондензатора в равенство [6] съдържа като множител i - имагинерната единица.
Тя, като комплексно число, може да се изрази чрез формулата на Ойлер за експоненциална
форма на комплексните числа:
 . [7]
. [7]
 Да го заместим в [6]:
Да го заместим в [6]:
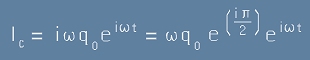 [8]
[8]
или по-кратко
 . [9]
. [9]
Съпоставката между това равенство [9] и по-горе [4] показват фазова разлика пи/2 (90 градуса) между тока и напрежението
през кондензатора. Това е очакван резултат, след като напрежението е пропорционално,
а токът - производна на функцията q(t).
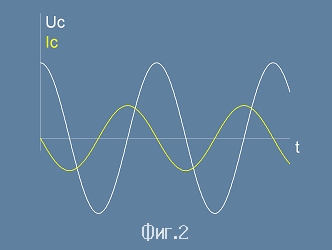
На фиг.2 Напрежението е изобразено (като косинусова функция - реалната част на комплексния израз) с бял цвят.
Токът е изобразен с жълт цвят (фазова добавка 90 градуса).
В условията на променливо напрежение и ток, отношението U/I - на напрежението в краищата на кондензатора към протичащия ток
се определя като
Импеданс на конензатора
- някъде за същото се използува израза "реактивно съпротивление", или "комплексно съпротивление".
Да го означим с Xc - за да го получим, разделяме [4] на [6]:
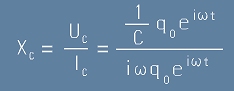 . [10]
. [10]
Следователно формулата за импеданс на кондензатора е
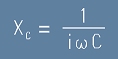 . [11]
. [11]
Както виждаме, импедансът зависи от честотата. За високочестотни токове кондензарирът има малък импеданс (съпротивление).
Ако честотата клони към нула, съпротивлението на кондензатора нараства безкрайно.
Да разгледаме сега случая, при който в елетричната верига участвува
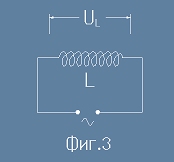
Индуктивност
(фиг.3) Напрежението в двата края на намотката е
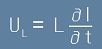 . [12]
. [12]
Токът се определя от същите съображения, както по-горе [5] и [6], тоест
 , [13]
, [13]
и след като заместим [13] в [12], напрежението е
 , [14]
, [14]
Да съпоставим това с фазово отместения ток, пресметнат както по-горе в [9]:
 . [15]
. [15]
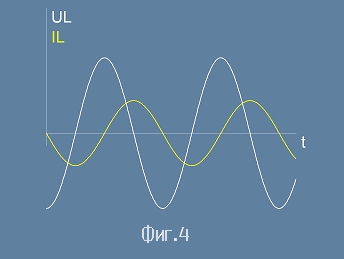 Отново виждаме фазово изместване, но знакът минус пред напрежението в [14] превръща и относителното фазово отместване
- то е с обратен знак на отместването, причинено от кондензатора по-горе.
Виж фиг.4 - бялата линия е напрежението (косинусова функция, съответна на реалната част), а жълтата - тока.
Тази разлика също идва от производната в израза [12].
Отново виждаме фазово изместване, но знакът минус пред напрежението в [14] превръща и относителното фазово отместване
- то е с обратен знак на отместването, причинено от кондензатора по-горе.
Виж фиг.4 - бялата линия е напрежението (косинусова функция, съответна на реалната част), а жълтата - тока.
Тази разлика също идва от производната в израза [12].
Отношението U/I - на напрежението в краищата на намотката към протичащия ток
се определя като
Импеданс на намотката
- понякога "реактивно съпротивление", или "комплексно съпротивление" на намотката (соленоида).
Заместваме U и I от [14] и [13]
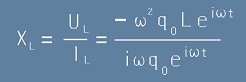 , [16]
, [16]
или по-кратко
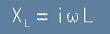 . [17]
. [17]
И това зависи от честотата. При малки честоти импедансът на намотката клони към нула,
но за високочестотни напрежения тя е почти непроходима, тъй като импедансът расте неограничено.
коментари
Радостин Желязков 08.06.2011
________________________________________________________________________________________
учебни статии по физика
 Променлив ток
Променлив ток
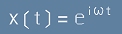 [1]
[1]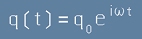 , [2]
, [2] Кондензаторът
Кондензаторът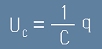 , [3]
, [3]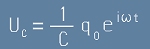 . [4]
. [4]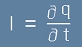 , [5]
, [5]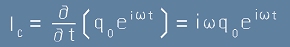 . [6]
. [6] . [7]
. [7] Да го заместим в [6]:
Да го заместим в [6]: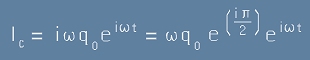 [8]
[8]  . [9]
. [9] 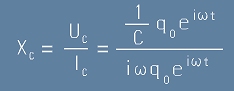 . [10]
. [10]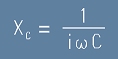 . [11]
. [11]
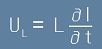 . [12]
. [12] , [13]
, [13] , [14]
, [14] . [15]
. [15] Отново виждаме фазово изместване, но знакът минус пред напрежението в [14] превръща и относителното фазово отместване
- то е с обратен знак на отместването, причинено от кондензатора по-горе.
Виж фиг.4 - бялата линия е напрежението (косинусова функция, съответна на реалната част), а жълтата - тока.
Тази разлика също идва от производната в израза [12].
Отново виждаме фазово изместване, но знакът минус пред напрежението в [14] превръща и относителното фазово отместване
- то е с обратен знак на отместването, причинено от кондензатора по-горе.
Виж фиг.4 - бялата линия е напрежението (косинусова функция, съответна на реалната част), а жълтата - тока.
Тази разлика също идва от производната в израза [12].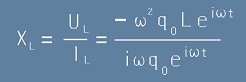 , [16]
, [16]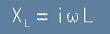 . [17]
. [17]