 Ефект на Комптън
Ефект на Комптън
Това е важен момент от историята на квантовата теория.
Артур Комптън го е публикувал през май 1923 г, в списание "Физикъл ревю",
докато е работил в университета Вашингтон в Сейнт Луис, САЩ - Мисури.
За тази си работа той е получил Нобелова награда по физика.
Изводът по-долу е съвременен и се отклонява малко от оригинала на Комптън.
Въздействието на светлината върху електроните е било известно доста преди това като
фотоелектричен ефект -
в който светлинен лъч избива електрони от повърхността на материала и ги превръща в свободни носители на електричен ток.
Тук са ползувани сведения, описани в предишни статии:
Теория на относителността - Материя,
Закон на Планк.
Гама-детектори
 Ние можем да мислим за гама излъчването като за електромагнитна вълна с висока честота.
Ние можем да мислим за гама излъчването като за електромагнитна вълна с висока честота.
В тази статия обаче е показан пример, който не може да бъде обяснен само като вълново явление.
Гама-лъчите имат висока пробивна способност. Те могат да бъдат забелязани само с посредничество на специални инструменти.
Сериозна част от работата по експеримента на Комптън се е състояла в разработване на подходящи прибори
и това в наши дни остава да е важно в Гама-измерванията.
Първите два вида Гама-детектори са Броячът на Гайгер и Кристалния Гама-сцинтилатор - базиран на Натриев йодид (NaI),
или други подобни вещества.
Гайгеровият брояч е чуден прибор, регистриращ Гама-порции чрез умножено усилване на йонизиращия им ефект.
Той показва Гама излъчването дискретно, като брой импулси, но не и като непрекъсната стойност на енергията.
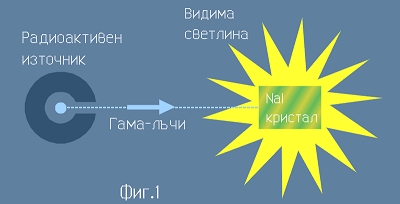
За разлика от него, Гама-сцинтилатора е кристал, който има свойство, че ако бъде облъчен с Гама-лъчи,
излъчва видима светлина (Фиг.1),
или други вторични електромагнитни вълни. Вторичното лъчене се привежда към пропорционално
електрично напрежение - с фотоелектрични преобразуватели. Интензитетът му нараства заедно
с нарастването на първичната Гама-енергия. Затова детекторите, базирани върху искрящи (сцинтилаторни) кристали, могат не само да регистрират,
но и да отмерват енергията (и заедно с това - честотатата) на Гама-лъчите.
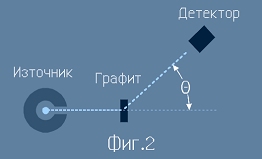
Опитна постановка
Експериментът на Комптън изследва разсейването на Гама-лъчи с които е било облъчвано
опитно вещество-графит. Схема на постановката е изобразена на Фиг.2.
В опита се измерва честотата на разсейваните от графита Гама-лъчи.
Тази честота, разпределена по ъгъла на разсейване - означен с гръцка буква Тита - представлява зависимост, обяснена от извода по-долу.
Честотата е била измервана по вторично излъчване, с кристален Гама-детектор, какъвто е описан по-горе.
Квантов модел
Комптън приема, че Гама-енергията е съставена от кванти (двойнствено с вълните) и разглежда удар между един-единствен
Гама-квант и един електрон от вътрешността на графита. Преди удара електронът е неподвижен,
но Гама-частицата отдава малко от енергията си, след което електронът напуска тялото, а вторичният Гама-квант се регистрира от детектора.
Двете частици имат собствена енергия и импулс, чрез които Комптън
прави разчет за връзката между ъгъл на разсейване и честотата на разсеяните Гама-лъчи.
Както беше споменато по-горе, Гама-лъчите носят висока енергия. Електрон, поел част
от такава енергия, придобива скорост над пределите на класическата механика. Затова Комптън прави
пресмятането чрез
Релативистко представяне
на енергиите и импулсите на двете частици. Съгласно теорията на относителността, енергията
на частица в покой е E=mc2, където с m е означена маса в покой.
При движение със скорост v, дясната страна на тази формула трябва да е умножена по Лоренцовия фактор
(виж [7] и [8] от статията "Материя"
в раздела Теория на относителността).
По-долу с наклонена буква m е означена масата при движение със скорост v.
С формула, енергията на частицата при движение със скорост v е
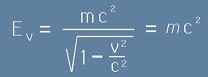 , [1]
, [1]
където - пак да кажем - m е маса в покой, а m - маса в движение.
Второто равенство от [1], умножено по знаменателя и повдигнато на втора степен води до
 . [2]
. [2]
Да означим с P=mv импулса на частицата. Виждаме, че последният член от [2] е:
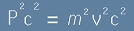 . [3]
. [3]
Горните три равенства показват, че
 , [4]
, [4]
където отляво Ev е енергията в движение, а отдясно m2c4 - енергия в покой.
Буква P означава импулс на частицата.
Светлинните кванти нямат маса в покой и съгласно [4] енергията им е E=Pc.
Имайки предвид и формулата на Планк E=hf
(
виж [18] от статията за Планк
)
,
Комптън изразява импулса на един Гама-квант като
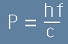 . [4.1]
. [4.1]
 Формула за разсейването
Формула за разсейването
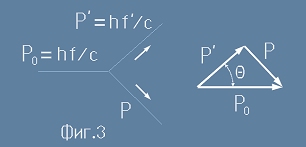
Приема се, че преди удара електронът е неподвижен. На фиг.3 има схема на удара,
близка до оригиналния чертеж на Комптън.
Импулсите са представени само като големини,
защото оценката по-долу е геометрична - съгласно косинусовата теорема
 , [5]
, [5]
където P0 е импулса на началния Гама-квант, P' е импулса на разсеяния Гама-квант,
а P е импулса, придобит от електрона след удара. С гръцка буква Тита е означен ъгъла на разсейване на гама-кванта.
Ако ползуваме [4.1], горното е еквивалент на
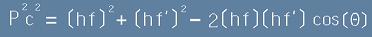 . [5.1]
. [5.1]
Сборът на енергиите преди и след удара трябва да е еднакъв. Значи
 , [6]
, [6]
където вляво hf е енергията на началния Гама-квант, mc2 е енергията на неподвижния електрон,
а в дясно hf' е енергията на разсеяния Гама-квант, Ev е енергията на отскочилия електрон.
Последното равенство [6] може да бъде записано като
 . [7]
. [7]
Ако повдигнем на квадрат [7],
в лявата страна ще остане израз, който можем да заместим според [4] от по-горе:
 . [8]
. [8]
Да означим с L и R лявата и дясната страна на [8] и да вземем предвид [5.1]:
 , [9]
, [9]
 . [10]
. [10]
След като премахнем еднаквите събираеми и приравним отново L и R, ще получим:
 . [11]
. [11]
Да разделим двете страни на 2 h f f ' m c:
 . [12]
. [12]
Имайки предвид, че c/f всъщност е дължината на вълната, получаваме обещаната
формула за разпределение на разсеяните Гама-кванти като зависимост дължина на вълната от ъгъла
на разсейване:
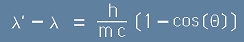 . [13]
. [13]
В тази формула с малка гръцка Ламбда е означена дължината на вълната (като прим е означение за разсеяниат квант),
m е масата на електрона, h - константата на Планк, Тита е ъгъла на разсейване. Това е било потвърдено
от опита на Комптън.
Радостин Желязков 15.09.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Ефект на Комптън
Ефект на Комптън
 Ние можем да мислим за гама излъчването като за електромагнитна вълна с висока честота.
Ние можем да мислим за гама излъчването като за електромагнитна вълна с висока честота.
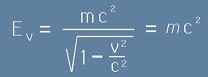 , [1]
, [1] . [2]
. [2]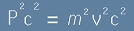 . [3]
. [3] , [4]
, [4]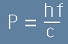 . [4.1]
. [4.1] Формула за разсейването
Формула за разсейването , [5]
, [5]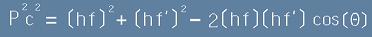 . [5.1]
. [5.1] , [6]
, [6] . [7]
. [7] . [8]
. [8] , [9]
, [9] . [10]
. [10] . [11]
. [11] . [12]
. [12]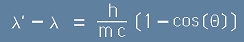 . [13]
. [13]