 Закон на Планк
Закон на Планк
Това е статия номер едно от квантовата физика.
Изведена е формулата, с която Планк описва излъчването на абсолютно черно тяло.
Планк публикува тази си работа около 1900 г.
Не са ми известни подробностите от публикацията на Планк -
в този извод, ходът на разсъжденията вероятно се отклонява от оригинала.
Тук са използувани знания от статиите
Идеален газ,
Теорема на Лиувил,
Разпределение на Максуел-Болцман,
Уравнение на Хамилтон,
Стълба на Габриел.
Трябва също да имате представа за
Електромагнитни вълни
и хармоничния осцилатор от статията Трептящ кръг.
История
 По времето, когато Планк е работил над тази формула, светлината и топлинното излъчване са били
смятани за чисто вълново явление, представено от теорията на Максуел и опитите, които я потвърждават.
Думата "фотон" възниква години по-късно (1926-1927, Г.Люис и А. Комптън).
Преди Планк да публиква своя резултат, е имало две практични описателни формули, за които се е знаело,
че покриват само отделни части от спектъра.
По времето, когато Планк е работил над тази формула, светлината и топлинното излъчване са били
смятани за чисто вълново явление, представено от теорията на Максуел и опитите, които я потвърждават.
Думата "фотон" възниква години по-късно (1926-1927, Г.Люис и А. Комптън).
Преди Планк да публиква своя резултат, е имало две практични описателни формули, за които се е знаело,
че покриват само отделни части от спектъра.
Планк е търсил теоретично обяснение за спектъра на топлинното излъчване, разглеждайки така нареченото
Абсолютно черно тяло
Това е кухина, в която интересното съдържание са единствено електромагнитните вълни.
Всяка точка от повърхността излъчва и поглъща такива вълни (фиг.1).
В резултат от многократните отражения, целият обем е запълнен с вълнови фронтове,
с различна честота и посока. Предполага се топлинно равновесие, тоест излъчваната и поглъщаната енергия са еднакви.
Равновесието предполага също, че вълните в тялото са стоящи.
Формата на кухината няма значение.
Тук ще приемем - както изследователите от времето на Планк - че електромагнитните трептения в кухината се моделират
чрез трептящи елементи, наричани осцилатори. Осцилаторите изразяват представата,
че вълновия процес е предаване на движение от едно към друго съседно място.
Всяка област от обема на тялото с размери колкото една дължина на вълната, сама по себе си е осцилатор.
Това е било в съгласие с хипотезата на Максуел за ефира - материална среда, в която се пренасят електромагнитните вълни.
Максуел е вярвал, че ефирът е съставен от микроелементи със специални свойства, които допускат осцилации.
По-долу се говори за плътност и статистическо разпределение именно на осцилатори. Но дали съществуват
такива обекти, или не - това не е критично за извода. Ако Ви е по-удобно, вместо за осцилатор, мислете
за режим на електромагнитно колебание, какъвто без съмнение има при всяка електромагнитна вълна.
 Честотно пространство
Честотно пространство
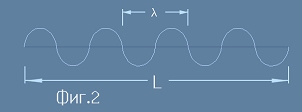
Да означим с малка гръцка буква ламбда дължината на една стояща вълна. Да разгледаме за удобство куб
с разстояние L между две срещуположни стени (фиг.2). Можем да смятаме, че това разстояние е по x-направление.
По отсечката L се нанасят цял брой полувълни:
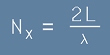 . [1]
. [1]
и всяка от тях съответствува на честота, с която трепти един осцилатор. Числото Nx заема цели стойности 1,2,3, ...
От горното равенство [1], ламбда може да се изрази като
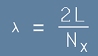 . [2]
. [2]
Нека c е скоростта на светлината, а f - честотата.
Тогава 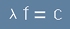 [3] , тоест
[3] , тоест
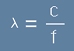 . [4]
. [4]
Десните страни на [2] и [4] трябва да са равни: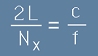 [5], откъдето следва, че
[5], откъдето следва, че
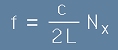 . [6]
. [6]
Линейната връзка [6] между цялото число Nx и честотата,
показва известното правило, че честотите на стоящите вълни (както в струна) се отнасят като цели числа 1,2,3, ...
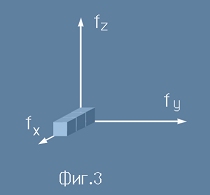
Да построим линейно честотно пространство, съставено от три направления -
fx, fy, fz - виж фиг.3. Тъй като Nx е число, коефициентът c/2L от [6] има размерност на честота
и може да се третира като честотен интервал с големина единица.
От [6] се вижда, че за всяко следващо Nx трябва да прибавим c/2L към предната честота.
В такъв случай, кубче от честотното пространство със страна c/2L съответствува на честотен обем
V1f,
в който се съдържа една реална честота:
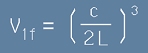 . [7]
. [7]
Разпределение
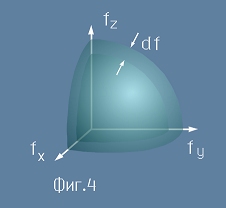
В честотното пространство, честотите с големина между f и f+df образуват сферична черупка с радиус f
и дебелина df - виж фиг.4. Вземаме предвид една осма от пълната сфера, защото честотите
и по трите направления са само положителни. Да означим с dV0 обема на черупката от фиг.4,
съответствуващ на брой честоти между f и f+df. Този обем е :
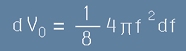 . [8]
. [8]
Но за една и съща честота са възможни две взаимно перпендикулярни поляризации,
така, че броя на режимите за осцилация са двойно повече от посоченото в [8].
Затова броя на реалните осцилатори в черупката - означен по-долу с dN - ще бъде равен удвоения брой от [8],
разделен на честотния обем за една честота V1f - пресметнат по-горе в [7].
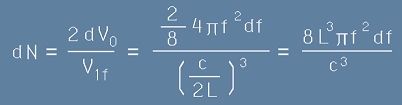 . [9]
. [9]
Да заместим третата степен на линейния размер с обема V на тялото: L3=V.
Ако с N(f) означим вероятностното разпределение на осцилаторите по честота, то
броя осцилатори с честоти между f и f+df ще е
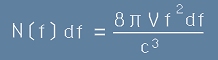 , [10]
, [10]
а отношението [10] към обема на кухината V е обемна плътност на разпределението - означение g ( f ) :
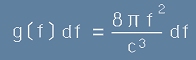 . [11]
. [11]
Енергия
Разпределението g от [11] е режими на осцилация по честоти. Но да не забравяме, че главната цел е
спектъра на топлинно излъчване за абсолютно черното тяло. Нещо, което знаем за топлинната
енергия на микрочастици е
равенство [11] от статията Идеален газ.
В него едноатомния газ има (3/2)kBT средна
кинетична енергия. Множителя 3/2 идва от трите степени на свобода на движение.
Но съгласно Теоремата на Лиувил,
вероятностите са разпределени равномерно по всяка ос на фазовото
пространство. От друга страна, в статията
Уравнение на Хамилтон
има илюстрация, как хармоничния осцилатор
се изобразява като фазова окръжност - тоест осцилатора има две фазови измерения. Един режим на осцилация от тези, които разпределяхме по-горе в [11],
е еквивалент на хармоничен осцилатор и следователно има две степени на свобода - за всяка от които се полага (1/2)kBT.
С други думи, бихме могли да предположим, че всеки един осцилатор има енергия kBT
- това в действителност се е случило. Разпределителната функция
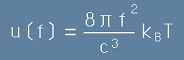 [12]
[12]
е известна в историята като формула на Рейли-Джийнс за спектъра на абсолютно черно тяло.
Тя е била полузвана за кратко време, но опитът е показал, че тази формула е приблизително вярна, само за ограничена област от спектъра.
Уточнение
Може би Планк е разсъждавал така: Всеки, ама всеки осцилатор да има една и съща енергия kBT е плоско допускане.
Но знаем, че той се е досетил - тези енергии, вместо да са еднакви, както е в [12],
трябва да бъдат случайно разпределени - подобно на Разпределението на Максуел-Болцман.
Заедно с това той е предположил, че енергията се формира от малки еднакви количества, право пропорционални на честотата f.
Това позволява множителя kBT в [12] да бъде заменен с
нормирана функция на разпределение за енергията на един осцилатор.
Да означим с  енергията на осцилатор с индекс N.
В такъв случай разпределената средна енергия на един осцилатор би изглеждала така:
енергията на осцилатор с индекс N.
В такъв случай разпределената средна енергия на един осцилатор би изглеждала така:
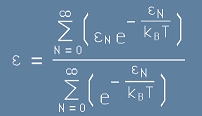 . [13]
. [13]
Съгласно предположението на Планк, индексираните стойности на енергиите  се отнасят като цели числа 0,1,2,3, ... ,
се отнасят като цели числа 0,1,2,3, ... ,
тоест ако  е първото от тях, N-тото ще е
е първото от тях, N-тото ще е
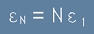 . [14]
. [14]
Събираемото с индекс 0 от сбора на знаменателя на [13] е експонента с нулев показател и е равно на 1.
Да означим с буквата q събираемото с индекс 1 от същия сбор:
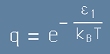 , после
, после
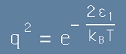 и изобщо
и изобщо
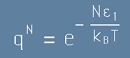 . [15]
. [15]
По този начин знаменателят на [13] се свежда до сбора
S=1+q+q2+q3+...
, известен под името Геометрична прогресия.
Числителят на [13] е също известен сбор
G=0+q+2q2+3q3+...
, наречен с името Стълба на Габриел.
След като знаeм какви са горните два сбора, да ги заместим в [13]:
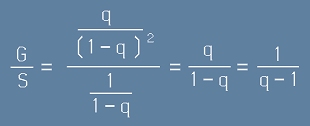 . [16]
. [16]
Да заместим обратно q от [15]. Тогава средната разпределена енергия за една осцилация от [13] става:
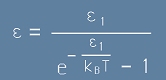 . [17]
. [17]
Кванти
В горното равенство остана условно означената енергия
 , от която следват останалите събираеми в сборовете на [13].
, от която следват останалите събираеми в сборовете на [13].
Съгласно уточнението, описано в предната точка, Планк е обявил равенството
 . [18]
. [18]
наречено Равенство на Планк - Айнщайн.
В него с буква f е означена честотата. С буква h е означена Константата на Планк - възникваща като пропорция.
Тази константа - h - има размерност [енергия] x [време] = Джаул по Секунда.
Физическият й смисъл е действие.
Енергията в лявата страна на [18] е най-малкото събираемо от сборовете на числителя и знаменателя във формулата [13].
Тази енергия -  - съгласно допускането на Планк
е най-малката възможна порция електромагнитна енергия - сега я наричаме квант - излъчвана от тялото.
- съгласно допускането на Планк
е най-малката възможна порция електромагнитна енергия - сега я наричаме квант - излъчвана от тялото.
Да забележим, че квантът енергия е фиксиран само при конкретна честота.
Планк е използувал думата "пакет". Малко по-късно Айнщайн го е нарекъл "светлинен квант".
Спектър
 Да заместим [18] в [17] и после с полученото да заместим kBT в [12]:
Да заместим [18] в [17] и после с полученото да заместим kBT в [12]:
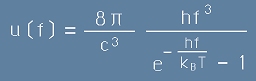 . [19]
. [19]
Това е Закона на Планк за спектъра на електромагнитното излъчване от абсолютно черно тяло.
В тази формула f е честотата на електромагнитните вълни, а T е абсолютната температура,
функцията u ( f ) е спектрална плътност, отнесена към единица обем.
h е константата на Планк,
kB е константата на Болцман,
c е скоростта на светлината.
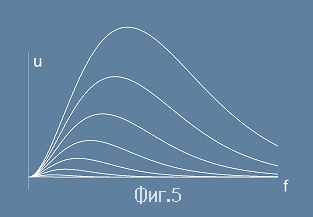
На фиг.5 са показани няколко криви на функцията u ( f ) - съответни на нарастващи температури.
коментари
Радостин Желязков 25.05.2011
________________________________________________________________________________________
учебни статии по физика
 Закон на Планк
Закон на Планк
 По времето, когато Планк е работил над тази формула, светлината и топлинното излъчване са били
смятани за чисто вълново явление, представено от теорията на Максуел и опитите, които я потвърждават.
Думата "фотон" възниква години по-късно (1926-1927, Г.Люис и А. Комптън).
Преди Планк да публиква своя резултат, е имало две практични описателни формули, за които се е знаело,
че покриват само отделни части от спектъра.
По времето, когато Планк е работил над тази формула, светлината и топлинното излъчване са били
смятани за чисто вълново явление, представено от теорията на Максуел и опитите, които я потвърждават.
Думата "фотон" възниква години по-късно (1926-1927, Г.Люис и А. Комптън).
Преди Планк да публиква своя резултат, е имало две практични описателни формули, за които се е знаело,
че покриват само отделни части от спектъра. Честотно пространство
Честотно пространство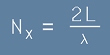 . [1]
. [1]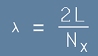 . [2]
. [2]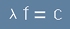 [3] , тоест
[3] , тоест
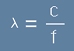 . [4]
. [4]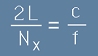 [5], откъдето следва, че
[5], откъдето следва, че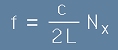 . [6]
. [6]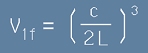 . [7]
. [7]
 . [8]
. [8]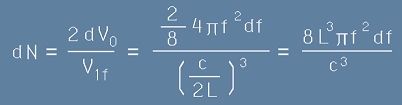 . [9]
. [9]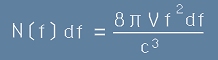 , [10]
, [10]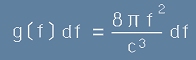 . [11]
. [11]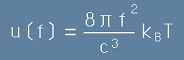 [12]
[12] енергията на осцилатор с индекс N.
В такъв случай разпределената средна енергия на един осцилатор би изглеждала така:
енергията на осцилатор с индекс N.
В такъв случай разпределената средна енергия на един осцилатор би изглеждала така: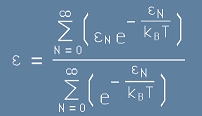 . [13]
. [13] се отнасят като цели числа 0,1,2,3, ... ,
се отнасят като цели числа 0,1,2,3, ... , е първото от тях, N-тото ще е
е първото от тях, N-тото ще е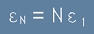 . [14]
. [14]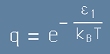 , после
, после
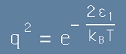 и изобщо
и изобщо
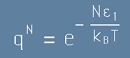 . [15]
. [15]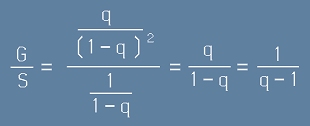 . [16]
. [16] . [17]
. [17] , от която следват останалите събираеми в сборовете на [13].
, от която следват останалите събираеми в сборовете на [13]. . [18]
. [18] - съгласно допускането на Планк
е най-малката възможна порция електромагнитна енергия - сега я наричаме квант - излъчвана от тялото.
- съгласно допускането на Планк
е най-малката възможна порция електромагнитна енергия - сега я наричаме квант - излъчвана от тялото. Да заместим [18] в [17] и после с полученото да заместим kBT в [12]:
Да заместим [18] в [17] и после с полученото да заместим kBT в [12]: . [19]
. [19]