 Теорема на Лиувил
Теорема на Лиувил
Текстът по-долу трябва да се третира като част от класическата термодинамика.
Добре е да сте запознати със статиите
Уравнения на Максуел,
Уравнения на Хамилтон,
Разпределение на Максуел-Болцман
Уравнение на Поасон,
Набла операции.
Фазов флуид
 В статията
Уравнения на Хамилтон
е споменато какво е фазово пространство. Но да повторим. Да приемем, че обобщеното пространство е 3-мерно.
Координатите на една материална точка са три числа. Векторът на обобщения импулс има координати,
които са други три числа. Общо 6-те координатни числа съставят точка (вектор) от фазово пространство.
Ако разглеждаме много материални точки във фазовото пространство, всяка от тях ще се изобрази
чрез 6-мерен фазов вектор. Да допуснем за миг, че координатите и импулсите на частиците заемат само
дискретни стойности - състояния. Да означим с
В статията
Уравнения на Хамилтон
е споменато какво е фазово пространство. Но да повторим. Да приемем, че обобщеното пространство е 3-мерно.
Координатите на една материална точка са три числа. Векторът на обобщения импулс има координати,
които са други три числа. Общо 6-те координатни числа съставят точка (вектор) от фазово пространство.
Ако разглеждаме много материални точки във фазовото пространство, всяка от тях ще се изобрази
чрез 6-мерен фазов вектор. Да допуснем за миг, че координатите и импулсите на частиците заемат само
дискретни стойности - състояния. Да означим с
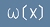 гъстотата на възможните състояния за фазова точка x.
гъстотата на възможните състояния за фазова точка x.
Ако с dx означим малък фазов обем около точката x, броя на състоянията в този обем ще е
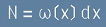 . [1]
. [1]
При преход от дискретни към непрекъснати стойности на фазовите координати,
буквата N от формула [1] ще означава вероятност системата да е състояние,
което попада вътре във фазовият обем dx, а функцията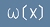 ще има смисъл на вероятностно разпределение (Какво е вероятностностно разпределение пише в
статията Разпределение на Максуел-Болцман ).
Промяната в състоянието на една частица може да се изобрази
като траектория във фазовото пространство (фиг.1).
Имайки предвид фазовите траектории на всички частици, можем да разглеждаме промените на системата във времето
като поток на флуид с плътност
ще има смисъл на вероятностно разпределение (Какво е вероятностностно разпределение пише в
статията Разпределение на Максуел-Болцман ).
Промяната в състоянието на една частица може да се изобрази
като траектория във фазовото пространство (фиг.1).
Имайки предвид фазовите траектории на всички частици, можем да разглеждаме промените на системата във времето
като поток на флуид с плътност 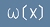 във фазовото пространство.
във фазовото пространство.
В предна статия - в равенство [24] от Уравнения на Максуел има разгледано
подобно движение - флуидът, който се движи там е електричен заряд -
и вместо омега се ползува друга буква - ро - плътност на заряда.
Повтяряме стъпките по онази статия. Първо да дефинираме аналог на плътността на тока:
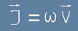 . [2]
. [2]
Където омега е вероятностната функция, а v е промяната на фазовия координатен вектор за единица време.
Буквата J в ляво на [2] ще има смисъл на вероятностен поток.
Тъй както при Максуел електричният заряд се запазва, така и тук, съгласно нормировъчното условие,
сбора на всички вероятности във фазовия обем V е константа =1.
 . [2.1]
. [2.1]
Да разгледаме затворен обем от фазовото пространство с повърхност S.
Както прилива на заряд през стените на тази повърхност доведе до увеличаване на заряда вътре в затворения обем,
така и тук
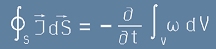 . [2.2]
. [2.2]
Знакът минус в дясно означава, че сме избрали затворената повърхност да е ориентирана навън
- нормалният вектор към повърхността да съвпада по посока с извиращия вектор J.
Вектора J трябва да спазва теоремата за дивергенцията (виж статията
Уравнение на Поасон) :
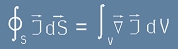 . [2.3]
. [2.3]
Десните страни на [2.2] и [2.3] трябва да са равни - така стигаме до аналог на равенство [24] от Максуел:
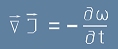 . [3]
. [3]
Изобщо това равенство - [3] - е известно под името
Теорема за непрекъсност
Тази теорема се превежда в наш контекст така: Колкото флуид извира от границата на затворения обем,
с толкова се намалява количеството (и съответно плътността) му вътре в обема.
Да заместим [2] в [3]:
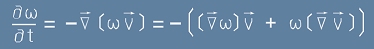 . [4]
. [4]
Да не забравяме, че векторът v е съставен от производните на p и q по времето:
 .
.
Освен това,
набла-операторът
от [3] и [4], за фазовото пространство ще има вид
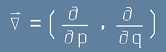 ,
,
така, че двете събираеми от скобите в [4] са
първо: 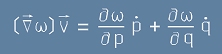 [4.1]
[4.1]
и второ: 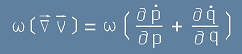 . [4.2]
. [4.2]
Имайки предвид [4.1] и [4.2], вместо [4] можем да напишем
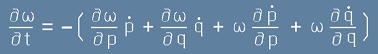 . [5]
. [5]
Да разгледаме последните две събираеми от [5]. Използувайки
каноничните уравнения на Хамилтон,
виждаме, че
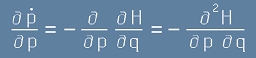 и още
и още
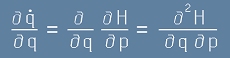 , [6]
, [6]
тоест те ще се унищожат и в [5] ще останат само първите две:
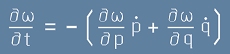 . [7]
. [7]
Вероятностната плътност - означена с омега - е функция на времето, обобщените координати и импулси.
Следователно нейната
Пълна производна
спрямо времето е
 . [8]
. [8]
Но съгласно [7], дясната страна на това равенство е нула. Значи и лявата е нула.
Това означава, че вероятностната функция омега е константа.
В това се състои споменатата в заглавието
Теорема на Лиувил
Тя гласи: Вероятностното разпределение на състоянията е равномерно по цялото фазово пространство.
С други думи: Всички състояния са равновероятни.
коментари
Радостин Желязков 13.05.2011
________________________________________________________________________________________
учебни статии по физика
 Теорема на Лиувил
Теорема на Лиувил
 В статията
Уравнения на Хамилтон
е споменато какво е фазово пространство. Но да повторим. Да приемем, че обобщеното пространство е 3-мерно.
Координатите на една материална точка са три числа. Векторът на обобщения импулс има координати,
които са други три числа. Общо 6-те координатни числа съставят точка (вектор) от фазово пространство.
Ако разглеждаме много материални точки във фазовото пространство, всяка от тях ще се изобрази
чрез 6-мерен фазов вектор. Да допуснем за миг, че координатите и импулсите на частиците заемат само
дискретни стойности - състояния. Да означим с
В статията
Уравнения на Хамилтон
е споменато какво е фазово пространство. Но да повторим. Да приемем, че обобщеното пространство е 3-мерно.
Координатите на една материална точка са три числа. Векторът на обобщения импулс има координати,
които са други три числа. Общо 6-те координатни числа съставят точка (вектор) от фазово пространство.
Ако разглеждаме много материални точки във фазовото пространство, всяка от тях ще се изобрази
чрез 6-мерен фазов вектор. Да допуснем за миг, че координатите и импулсите на частиците заемат само
дискретни стойности - състояния. Да означим с
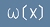 гъстотата на възможните състояния за фазова точка x.
гъстотата на възможните състояния за фазова точка x.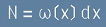 . [1]
. [1]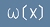 ще има смисъл на вероятностно разпределение (Какво е вероятностностно разпределение пише в
статията Разпределение на Максуел-Болцман ).
Промяната в състоянието на една частица може да се изобрази
като траектория във фазовото пространство (фиг.1).
Имайки предвид фазовите траектории на всички частици, можем да разглеждаме промените на системата във времето
като поток на флуид с плътност
ще има смисъл на вероятностно разпределение (Какво е вероятностностно разпределение пише в
статията Разпределение на Максуел-Болцман ).
Промяната в състоянието на една частица може да се изобрази
като траектория във фазовото пространство (фиг.1).
Имайки предвид фазовите траектории на всички частици, можем да разглеждаме промените на системата във времето
като поток на флуид с плътност 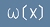 във фазовото пространство.
във фазовото пространство.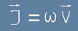 . [2]
. [2] . [2.1]
. [2.1]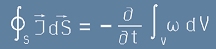 . [2.2]
. [2.2]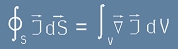 . [2.3]
. [2.3]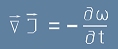 . [3]
. [3]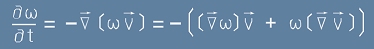 . [4]
. [4] .
.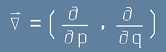 ,
,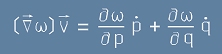 [4.1]
[4.1]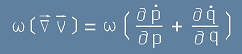 . [4.2]
. [4.2] 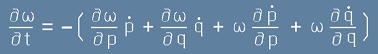 . [5]
. [5]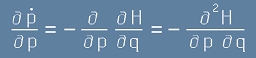 и още
и още
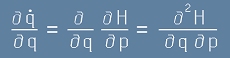 , [6]
, [6]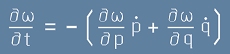 . [7]
. [7] . [8]
. [8]