 Разпределение на Максуел-Болцман
Разпределение на Максуел-Болцман
Това е част от класическата термодинамика, но изводът по-долу е съвременен.
Твърди се, че в историческия източник - оригинално от Дж.К.Максуел от 1860 и по-късно препечатан от Кембридж Юнивърсити Прес 1890,
видът на разпределението съвпада с показания по-долу в [21].
Добре е да сте запознати със статиите Идеален газ,
Барометрична формула,
Гаусови интеграли,
също със статията на Станчо Павлов
Инвариантност на първия диференциал на функция на повече променливи
.
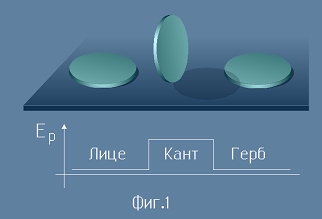
Зарове и монети
Когато хвърлим монета, тя пада с 1/2 вероятност на едната си страна.
Всъщност точната оценка включва и Кант - положение.
При него, центъра на тежестта на монетата и заедно с него - потенциалната енергия е по-високо,
отколкото за другите две възможности - затова то е по-малко вероятно.
По хоризонта на Фиг.1 са нанесесни трите възможности, които съставят т.нар.
пространство на събитията.
Ако означим с P1,P2,P3 вероятностите за трите възможни изхода, техният сбор ще е единица:
P1+P2+P3=1. [1]
Тук има две множества. Едното (Лице, Кант, Герб) е съставено от възможните събития (изходи след хвърлянето
на монетата), а другото (P1, P2, P3) - от вероятности, съответни на всеки елемент от първото
множество.
Това съответствие е всъщност функция, много близка по идея с така нареченото вероятностно
Разпределение
Описаната по-горе ситуация е върху дискретно множество от възможни събития.
При непрекъснати множества или пространства не е много по-сложно.
Нека с голяма гръцка буква Омега означим непрекъснато пространство
на събития - елементи означени с x. Условието за пълнота от [1] изглежда като интеграл:
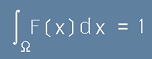 . [2]
. [2]
Подинтегралната функция F(x) се нарича вероятностно разпределение или вероятностна функция, или просто разпределение.
Съпоставката между [2] и [1] показва, че произведението
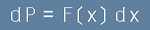 е вероятност за изход в интервала от x до x+dx , тоест
е вероятност за изход в интервала от x до x+dx , тоест
сама по себе си F - функцията НЕ Е ВЕРОЯТНОСТ, а има характер на "вероятностна плътност".
Молекулите на газа често се удрят помежду си. При всеки удар те променят скоростите си,
така, че в един момент между тях ще се намерят бързи и бавни.
Тук ще потърсим отговор на въпроса "Колко са бързите и колко са бавните частици?".
След казаното по-горе, такъв въпрос би звучал : Какво е вероятностното разпределение на молекулите
По скорости
Скоростта на една частица е вектор и се разлага на три взаимно перпендикулярни компоненти
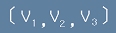 .
.
Да построим първа версия: разпределение по големина.
Големината на вектора на скоростта е  .
.
Разпределителната функция F зависи от големината на скоростта:
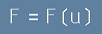 , но в крайна сметка F е функция на
v1, v2, v3 и следователно
, но в крайна сметка F е функция на
v1, v2, v3 и следователно
вероятността големината на една скорост да е в интервала u..u+du е
 . [3]
. [3]
Доказателство за вярността на [3] е дадено в страницата
"
Инвариантност на пълния диференциал
".
Да построим втора версия: разпределения по координатна ос.
Можем да обявим направленията на трите компоненти за координатни оси
и всяка скорост ще е точка в така полученото пространство на скоростите.
Да означим разпределението по първата координатна ос с
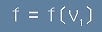 .
.
Вероятността първата компонента на една скорост да е между v1 и v1+dv1 е
произведение  . Аналогично важи и за другите две компоненти.
. Аналогично важи и за другите две компоненти.
Вероятността и трите компоненти да влязат в границите v..v+dv е произведението
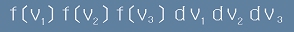 . [4]
. [4]
Двете вероятности [4] и [3] са върху едни и същи аргументни множества.
Те имат и един и същ смисъл. Разликата между тях е само в оста, върху която са проектирани скоростите -
това са две сенки на една и съща вероятност, която не може да зависи от посоката.
Приемаме, че
 , или по-кратко
, или по-кратко
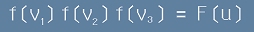 . [5]
. [5]
Да пресметнем производната на [5] по v1:
 [6] . Нека имаме предвид, че
[6] . Нека имаме предвид, че
 . от [6] получаваме
. от [6] получаваме
 . [7]
. [7]
Сега да разделим двете страни на последното уравнение [7] с двете страни на [5]:
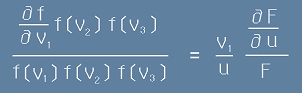 ,
,
или по-кратко
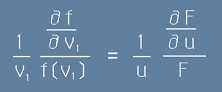 . [8]
. [8]
Изборът на координатното направление v1 е свободен - какъвто и да е той, [8] трябва да е вярно.
Това ни води до заключението, че всъщност двете страни на равенството [8] представляват константа.
Да означим тази константа с A. Тогава от [8] ще следва
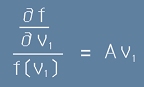 . [9]
. [9]
Интегралите на двете страни на [9] по v1 ще бъдат
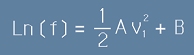 [10] , където B е друга константа, възникваща от интегрирането. Тогава функцията f ще е
[10] , където B е друга константа, възникваща от интегрирането. Тогава функцията f ще е
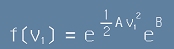 . [11]
. [11]
Ясно е, че когато скоростта клони към безкрайност, вероятността трябва да клони към нула. Щом е така,
константата A трябва да е отрицателна. За да гарантираме това, можем да я изместим с друга - такава, че A/2 = -b2.
Да заместим и константния множител eB = C. За функцията f остава формулата
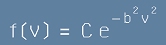 . [12]
. [12]
Тъй като [12] е вероятностно разпределение, трябва да е спазено условието за нормиране:
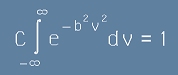 . [13]
. [13]
Да привлечем на помощ известното решение на Гаусовия интеграл нула I0
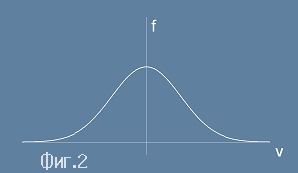
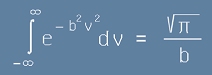 , тоест
, тоест
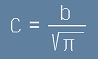 .
.
Без да уточняваме константата b, разпределението на молекулите по скорости е
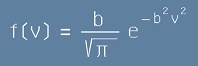 . [14]
. [14]
Такъв тип рапределение се нарича Нормално или Гаусово разпределение.
Функцията f е симетрична спрямо правата v=0, тъй като скоростите "напред" и "назад" по кое да е направление
са равновероятни и векторният сбор от всички скорости е нулев. Графиката f(v) е показана на Фиг.2 - Нарича се Гаусова крива.
* * *
Сега ще намерим разпределението на молекулите
По енергия
Енергията е пропорционална на квадрата на скоростта - тя не зависи от направлението,
а само от квадрата на вектора, означена по-горе с u. Да означим с N броя на всички възможни скоростни вектори.
(N не може да е по-голямо от броя на частиците).
Броя на скоростите чиято големина е в интервала u..u+du ще бъде
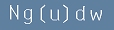 , [15]
, [15]
където dw е елементарен обем в пространството на скоростите, а g(u) e разпределението на скоростите в този обем.
Тъй като dw е участък скорости с почти еднакви големини u..u+du, то
елементарният обем dw е сферична черупка с радиус u и дебелина du :
 .
.
Вероятностното разпределение по трите координатни оси,
участвуващо по-горе като множител в [4] би трабвало да съвпада с g(u),
тъй като произведението на [4] по N
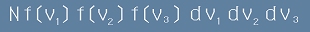 трябва да даде същият брой, какъвто е [15]:
трябва да даде същият брой, какъвто е [15]:
 .
.
По аналогия с [5] можем да смятаме, че
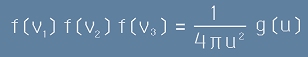 .
.
Но u е линейно направление, равноправно с трите скоростни оси и ако
v=u=v1, v2=0, v3=0,
получаваме
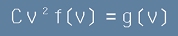 [16],
[16],
където C е константен множител. Знаем какво е осевото разпределение от [14],
следователно разпределението по квадрати трябва да е
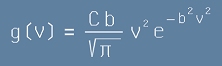 [17] .
[17] .
За да се нормира разпределението [17], тоест
 , [18]
, [18]
ще ни трябва решението на Гаусовият интеграл две I2 :
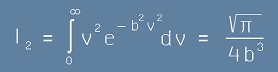 . [19]
. [19]
Константата C трябва да удовлетворява равенството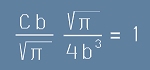 , [20]
, [20]
тоест C=4b2.
Заместваме това в [17] - там ще остане само една константа b и разпределението по квадрати на скоростите ще е
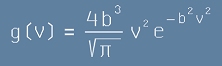 . [21]
. [21]
(мисля, че в оригинала на Максуел е било написано точно горното равенство [21]).
Остана да разберем каква е константата b.
Щом функцията g(v) е разпределение на квадратите на скоростите, можем да смятаме, че средният квадрат на скоростта е
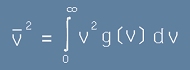 . [22]
. [22]
Съгласно равенство [11] от статията идеален газ, средният квадрат би трябвало да е
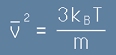 . [23]
. [23]
Заместваме g от [21] и слагаме знак за равенство между десните страни на [23] и [22].
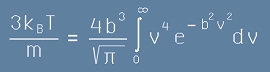 . [24]
. [24]
Да повикаме на помощ решението на Гаусовият интеграл I4 :
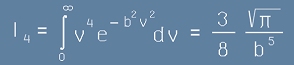 . [25]
. [25]
Заместваме [25] в [24]:
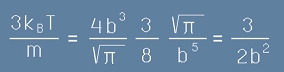 . [26]
. [26]
 и получаваме израз за неизвестната досега константа b :
и получаваме израз за неизвестната досега константа b :
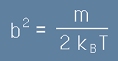 . [27]
. [27]
Заместваме го в [21] и получаваме обещаното най-горе
Разпределение на Максуел-Болцман
Формулата е:
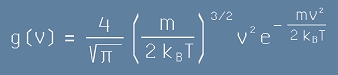 . [28]
. [28]
Това е разпределение на броя молекули по квадрати на скоростите, тоест по кинетична енергия,
m е масата на една молекула, kB е константата на Болцман, T е абсолютната температура.
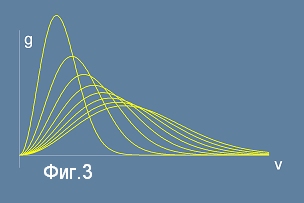
На Фиг.3 е показана поредица графики g(v) при нарастваща температура отляво надясно.
коментари
Радостин Желязков 29.04.2011
________________________________________________________________________________________
учебни статии по физика
 Разпределение на Максуел-Болцман
Разпределение на Максуел-Болцман

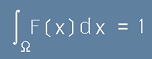 . [2]
. [2]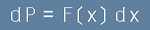 е вероятност за изход в интервала от x до x+dx , тоест
е вероятност за изход в интервала от x до x+dx , тоест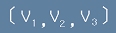 .
. .
.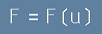 , но в крайна сметка F е функция на
v1, v2, v3 и следователно
, но в крайна сметка F е функция на
v1, v2, v3 и следователно . [3]
. [3]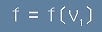 .
.  . Аналогично важи и за другите две компоненти.
. Аналогично важи и за другите две компоненти.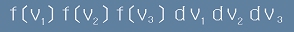 . [4]
. [4] , или по-кратко
, или по-кратко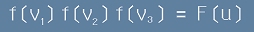 . [5]
. [5] [6] . Нека имаме предвид, че
[6] . Нека имаме предвид, че . от [6] получаваме
. от [6] получаваме
 . [7]
. [7]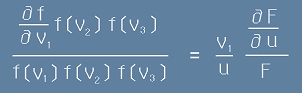 ,
,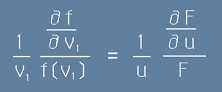 . [8]
. [8]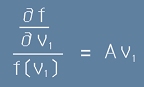 . [9]
. [9]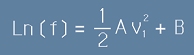 [10] , където B е друга константа, възникваща от интегрирането. Тогава функцията f ще е
[10] , където B е друга константа, възникваща от интегрирането. Тогава функцията f ще е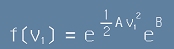 . [11]
. [11]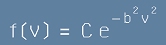 . [12]
. [12]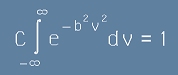 . [13]
. [13]
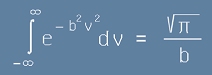 , тоест
, тоест
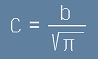 .
.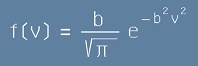 . [14]
. [14]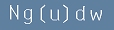 , [15]
, [15]  .
. 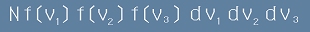 трябва да даде същият брой, какъвто е [15]:
трябва да даде същият брой, какъвто е [15]: .
.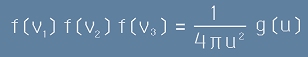 .
.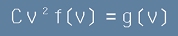 [16],
[16],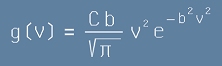 [17] .
[17] . , [18]
, [18]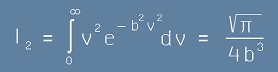 . [19]
. [19]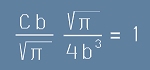 , [20]
, [20]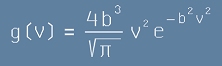 . [21]
. [21]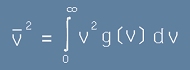 . [22]
. [22]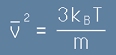 . [23]
. [23]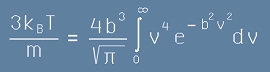 . [24]
. [24]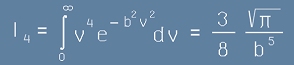 . [25]
. [25]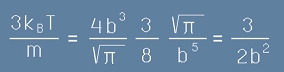 . [26]
. [26] и получаваме израз за неизвестната досега константа b :
и получаваме израз за неизвестната досега константа b :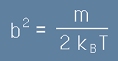 . [27]
. [27] . [28]
. [28]