 Уравнение на Шрьодингер
Уравнение на Шрьодингер
Публикувано е за първи път през 1926 г. и възбужда доста коментари, несъгласия и проблеми.
Години наред учените продължават да го коментират, да уточняват смисъла и решенията му.
Самият Шрьодингер е нямал добър отговор на въпроса какво точно представлява вълновата функция.
Той е имал предвид едно съвсем скромно решение. Сега са възникнали и други.
Много. много по-късно - през 1954 година Макс Борн получава Нобелова награда за тълкуването на Пси квадрат като вероятност
за присъствие.
Тук са ползувани предни статии:
Набла-операции,
Материални вълни.
Вълновата функция
както и Вълновият пакет са изобретени именно от Шрьодингер, заедно с уравнението по-долу.
За първи път в тази поредица, пакета е написан в статията "Материални вълни" равенство [17].
Ще го напишем и тук :
 , [1]
, [1]
С буква k е означен вълновия вектор, а с x-координатата. функцията f(k) е амплитудно разпределение.
Нека в горното уравнение, вместо k и x да заместим означенията
за импулса: 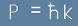 и за енергията:
и за енергията:
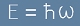 , [2]
, [2]
при това се сменя интегралната променлива от k към p и вълновият пакет изглежда по следния начин:
 . [3]
. [3]
Сега ще приемем нещо, на пръв поглед - естествено, а именно, че
Енергията и импулса се запазват
Това е вярно за една свободна частица.
Разбира се, това значи, че на p и E от [3] можем да гледаме като на константи.
Да пресметнем първата и втората частна производна на [3] спрямо координатата x:
първа:
 , [4]
, [4]
втора:
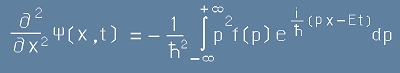 . [5]
. [5]
Да пресметнем също първата производна на [3] спрямо времето t:
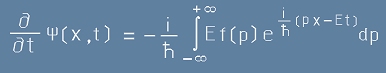 . [6]
. [6]
Шрьодингер е използувал класически израз за енергията, тоест
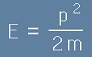 . [7]
. [7]
Да го заместим в [6]:
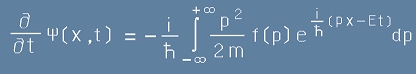 . [8]
. [8]
Дясната страна на [8] се различава от дясната страна на [5] само с множителя
 . [9]
. [9]
Ако умножим [5] по [9], ще получим [8].
Освен това, ако в по-горната линия [5] трябва да участвуват трите пространствени измерения
вместо само една x, ще трябва да сменим означението с набла на втора степен:
 . [10]
. [10]
Да запишем това явно:
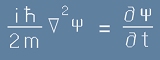 . [11]
. [11]
За се спазят размерностите от [7], трябва да умножим двете страни на [11] по имагинерната единица и по
 .
.
Така стигнахме и до
Уравнението на Шрьодингер
за свободна материална частица:
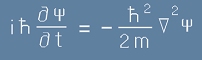 . [12]
. [12]
В това уравнение с буква Пси е означена Вълновата функция от по-горе [3], t - времето,
i е имагинерната единица, m е масата на частицата,
 е константата на Планк.
е константата на Планк.
Радостин Желязков 27.10.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Уравнение на Шрьодингер
Уравнение на Шрьодингер
 , [1]
, [1]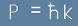 и за енергията:
и за енергията:
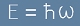 , [2]
, [2] . [3]
. [3] , [4]
, [4]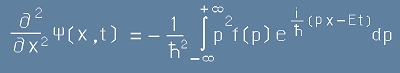 . [5]
. [5]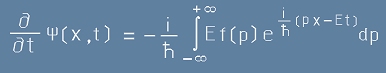 . [6]
. [6]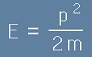 . [7]
. [7]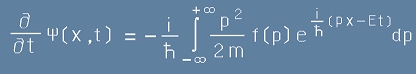 . [8]
. [8] . [9]
. [9] . [10]
. [10]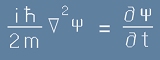 . [11]
. [11] .
.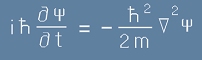 . [12]
. [12] е константата на Планк.
е константата на Планк.