 Материални вълни
Материални вълни
Тук става дума за вече успешната версия на Квантовата Механика - в "класическия" си вид. Тя се появява през 1923-1927 година,
след известните спорове в Копенхаген.
По времето, когато работят нейните създатели - Хайзенберг, Джордан, Макс Борн, Шрьодингер,
думата "фотон" почти не се използува. Това е съвременно изложение, отклоняващо се
значително от публикациите по онова време.
Тук са ползувани сведения от съседни статии:
Часовникът на Файнман,
Вълнови решения,
Електромагнитни вълни,
Плоска вълна,
Ефект на Комптън,
Закон на Планк.
Орбити и измервания
Представата за електрон, обикалящ по орбита е противоречива.
За да "видим" орбитално движение, би трябвала светлина с дължина на вълната, много по-малка
от радиуса на орбитата. Но такава светлина попада в Гама-спектъра и нейното въздействие върху
електроните е добре известно от
опита, описан в статията за Комптън.
При Гама-удар всеки електрон би напуснал
каква да е орбита и нашето изследване ще остане безсмислено.
Ясно е, че няма надежда за преки измервания, които да потвърдят или отхвърлят хипотезата за орбитално
движение на електрона. Ето как учените изоставят въобще идеята за траектория в микросвета.
Но ако прякото движение е ненаблюдаемо в атомната кутийка,
след прецедента за успешно дуалистично разглеждане "вълна/частица" - създаден от Комптън -
и след хипотезата на Дьо Бройл (същата година, в която е публикацията на Комптън - 1923),
съгласно която материалните частици могат да бъдат третирани като вълни,
да видим как изглежда идеята за
Вълнова природа
на микрочастиците. Първо ще направим важна уговорка -
нарисуваните по-долу и наричани с думи и формули вълни НЕ СА ЕЛЕКТРОМАГНИТНИ,
макар често да става дума за светлинни кванти и за електромагнитната теория.
Какви точно са тези вълни - по исторически и разумни причини е по-добре да изчакаме малко с отговора.
За тях се смята например, че са дисперсни. Това означава, че скоростта им на разпространение не е константа и зависи от честотата.
Заглавието на този текст ги нарича материални, но те нямат аналог в ежедневието.
Засега само ще търсим някакво решение на противоречието частица/вълна.
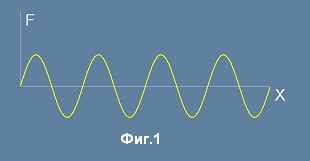
На Фиг.1 е показана синусова функция на един аргумент F=sin(x).
Ако си представим оста x като струна и съединим двата края на струната, ще получим
стояща затворена вълна върху окръжност - виж Фиг.2.
Така че, идейно казано, състоянията на електроните в атома, вместо като движения по траектории,
могат да бъдат описвани като стоящи вълни.
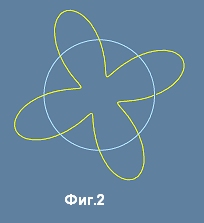
Детелината на Фиг.2 има точно 4 листа. Следователно струната в началото е била дълга 8пи (тоест четири периода).
За да е възможна такава вълна, по дължината на окръжността трябва да се нанасят цял брой периоди, като всеки период е 2пи.
Този брой създава важно целочислено условие, коментирано по-долу в този текст, в болд точка "Орбитални нива".
Да си спомним постановката за едномерно вълново уравнение - погледнете
равенства [7] и [10] от статията Електромагнитни вълни
:
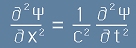 , [1]
, [1]
където c е скоростта на разпространение на вълната, x и t са координата и време, а с буква Пси е означена функция
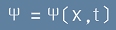 . [2]
. [2]
Има специална статия, в която е написан път за решаване на [1] -
"Вълнови решения" -
за да удовлетворява вълновото уравнение,
най-общо функцията Пси трябва да има вида:
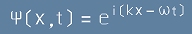 , [3]
, [3]
където множителите за пропорция пред времето-омега и пред координатата-k са вече споменавани
(виж равенства от [2] до [6] от "Плоска вълна"):
Буква омега означава ъглова честота:
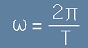 , [4]
с k е означено вълновото число:
, [4]
с k е означено вълновото число:
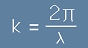 . [5]
. [5]
Тяхното отношение 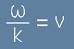 [5.1]
[5.1]
представлява скоростта на разпространение, което за електромагнитна вълна е равно на c.
Според формулата на Планк (виж
равенство [18] от статията "Закон на Планк"),
енергията, на кванта е
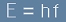 . [6]
. [6]
Да възприемем една нова версия (такава е конвенцията в квантовата механика) за константата на Планк:
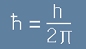 . [7]
. [7]
С това означение формулата на Планк има следния вид:
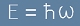 . [8]
. [8]
Но написаното дотук се отнася само за един-единствен осцилатор, който има определена честота - светлинен квант.
Дали е възможно по аналогичен начин да се представи материална частица, например електрон?
Да обърнем внимание и на споменатото по-горе k, наречено "вълново число".
То има връзка с честотата на вълната, заедно с това - и на енергията, а след правилото P=E/c
(виж
равенства [4] и [4.1] от статията Ефект на Комптън
),
значи и на импулса, асоцииран с тази вълна. Най-често k се нарича
Вълнов вектор
и представлява вектор с посока съвпадаща с посоката на разпространението на вълната,
а големината му е пропорционална на вълновия импулс:
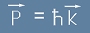 . [9]
. [9]
Написахме свързващата формула [9] между вълнов вектор и импулс, защото търсим връзка
между досегашната ни представа за движение на материална частица и предполагаемите й вълнови свойства.
Както току що отбелязахме, според [5], при плоската едноцветна вълна, представляваща светлинен квант,
вълновото число е твърдо зависимо от честотата.
Светлинните кванти имат скоростта на светлината и съгласно Теорията на Относителността, те присъствуват
едновременно в точката, от която възникват и точката, до която пристигат -
спомнете си как се синхронизират часовниците в две различни координатни системи
- това е описано в статията
"Часовникът на Файнман".
Честно казано, при тях за класическа скорост се говори трудно, защото dx/dt не определена, ако си представим,
че за едновременни събития dt=0.
Виж, енергия и импулс - имат - по формулите [8] и [9].
Но материалните частици са съвсем друго нещо. Техните скорости са осезаеми и по-малки от c.
Материалните частици имат позиция в пространството,
докато полето от [3] не е съсредоточено в никоя пространствена област.
Модулация
 Да разгледаме сбор две косинусови функции (защото такива съответствуват на реалната част от вълновото решение [3]).
Има едно известно тригонометричното тъждество за този случай:
Да разгледаме сбор две косинусови функции (защото такива съответствуват на реалната част от вълновото решение [3]).
Има едно известно тригонометричното тъждество за този случай:
 . [10]
. [10]
Ако Алфа и Бета са близки, симетрично разположени около точка Фи,
тоест
 , [11]
, [11]
то горното тъждество [10] се свежда до
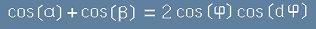 . [12]
. [12]
Да положим
 . [13]
. [13]
Тогава сборната функция изглежда така:
 . [14]
. [14]
Това е обикновена косинусова вълна с променяща се амплитуда пак
по косинусов закон, но с доста по-малка честота от основната - съответна на Фи.
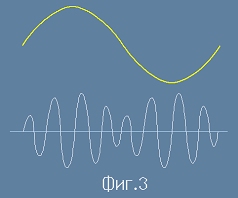
Резултатът е пулсираща синусоида, каквато е показана на Фиг.3.
Обвивката на вълната - като жълта крива - съотвествува по абсолютна стойност на амплитудата
от [13] и се променя като косинус с малка честота, а основната честота е съответна на аргумента Фи от [14].
Описната дотук процедура е известна в електротехниката под името модулация - начин
да се пренася информация чрез радиовълни.
Но какво би се случило, ако скоростите на двете съставни вълни
са различни? Тъй като по принцип началните аргументи от [10] Алфа и Бета се предполагат независими,
нито една от горните формули [10] ... [14] няма да се промени. Разликата ще се прояви като
ефект на "пълзене"
-
относително движение на амплитудната обвивка [13] спрямо основната вълна.
Това става само при дисперсни (не електромагнитни във вакуум) вълни и за тези случаи се дефинира специална
Групова скорост
Да върнем контекста към вълновото решение [3].
Степенния показател е функция на вълновия вектор (k) и ъгловата честота (омега).
Нека
 ,
и нека
,
и нека
 . [15]
. [15]
 Скоростта на разпространение е всъщност условие за нулева фаза - първото от двете [15].
Скоростта на разпространение е всъщност условие за нулева фаза - първото от двете [15].
Тази скорост е x/t=
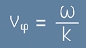 и се нарича още фазова скорост - същата е записана по-горе в [5.1].
и се нарича още фазова скорост - същата е записана по-горе в [5.1].
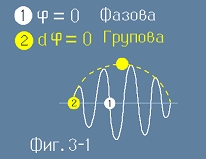
Нулева промяна на фазата - второто от [15] - представлява възел на обвиващата вълна.
Скоростта с която се придвижва тази точка е друга :
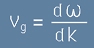 , [16]
, [16]
и се нарича групова скорост.
На фиг. 3-1 бялата точка (1) се движи с фазова скорост - това е скоростта на разпространение.
Двете жълти точки - възелът на обвивката (2), както и обвиващият максимум - се движат с групова скорост.
Суперпозиция
Решението, записано в [3] е подходящо за един-единстен светлинен квант. Обаче вълновото уравнение [1]
се подава на наслагване (суперпозиция). Това значи, че всяка линейна комбинация от функции-решения както Пси от [3],
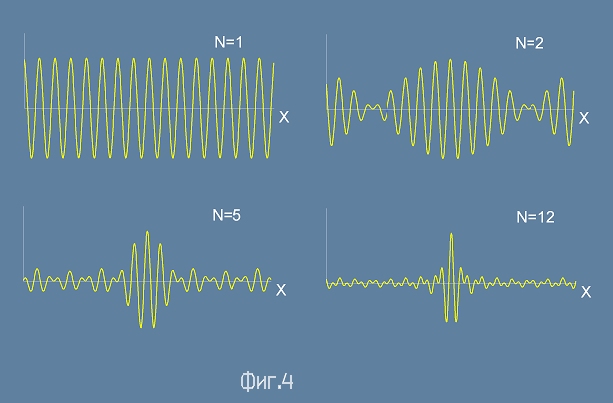
е също решение. Само като илюстрация направих една компютърна програма,
която изобразява сумата на няколко косинусови функции
с константно разпределен вълнов вектор - пропороционален на N
(виж по-долу за разпределението).
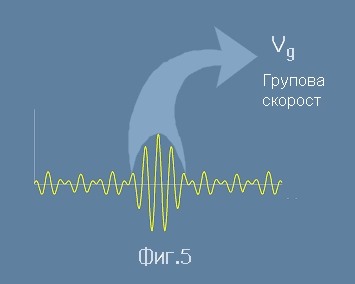
При нарастващ брой на събираемите (означен с буква N), тя показа картинките от Фиг.4.
От тях се вижда, че сборната вълна клони към позиционен максимум.
Това е начина, по който се съставя така наречения
Вълнов пакет
или понякога споменаван като вълнова група или вълнов влак (цуг,трен).
За да има ясен импулс, в един такъв пакет, е нужно
коефициентите в линейната комбинация да работят като разпределителна функция
f=f(k'), където k' е променлива, обхождаща множеството стойности на вълновия вектор k.
За едномерно пространство (само x-координата), това изглежда като интеграл:
 . [17]
. [17]
Линейна комбинация означава сбор
f1.e1+f2.e2+...+fn.en
,
където
f1, f2, ... fn
са коефициенти пред e-функциите.
Но когато e-функциите са комплексни - както е в нашия случай - е нормално да приемем,
че и f-коефициентите също са комплексни -
това би запазило решението на [1]. С други думи, приемаме, че f-разпределението е
 , [18]
, [18]
където сме предположили две други: амплитудна-A и фазова-Алфа функции, за да моделираме неизвестната f от [17].
Нека A(k') e функция на разпределение за амплитудите, която има максимум в стойността k'=k.
Избираме я така в името на съответствието между класическия импулс на материалната частица
и вълновия му еквивалент (пропорционален на k) според [9], очаквайки, че придвижването на пакета е еквивалент на класическо движение.
Ако заместим [18] в [17], подинтегралната функция ще е:
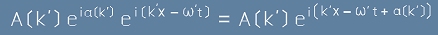 . [19]
. [19]
Да обявим ъгъл Фи като функция:
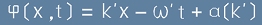 . [20]
. [20]
наречена фаза на пакета.
Тогава, вместо [17] можем да напишем:
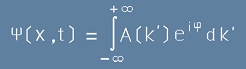 . [21]
. [21]
в което A e амплитудно разпределение,  е осцилираща експонента с фаза Фи,
е осцилираща експонента с фаза Фи,
а самата фаза (фи) е функция на k'.
Да допуснем, че в малка част от една осцилация на Пси,
аргументът фи запазва приблизително постоянна стойност за съседни k'.
Това означава, че и Пси ще се стабилизира около постоянна стойност спрямо k'.
Тези неща се случват в максимума и минимума.
Постоянна фаза Фи означава нулева производна спрямо k', в точка k'=k :
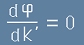 . [22]
. [22]
Но съгласно [20] производната на Фи е
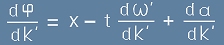 . [23]
. [23]
Условието от [22] е изпълнено в точка с x-координата
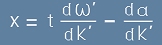 . [24]
. [24]
и тази точка се движи със скорост
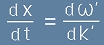 . [25]
. [25]
Същата тази скорост
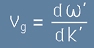 , [26]
, [26]
е всъщност груповата скорост от по-горе в [16].
Тя съответствува на движение на обвивката на вълновия пакет (Фиг.5).
Да видим как е свързано това с
Класическата представа
за движение. Съгласно нашата хипотеза, енергията и импулса на частицата трябва да са
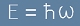 . [=8]
. [=8]
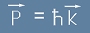 . [=9]
. [=9]
Класическата енергия на частица с маса m е :
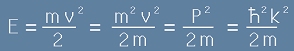 . [26.1]
. [26.1]
да приравним десните страни на [26.1] и [=8]:
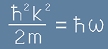 . [26.2]
. [26.2]
Получихме зависимостта на ъгловата честота от вълновия вектор:
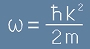 , [26.3]
, [26.3]
наричана някъде Дисперсно Отношение.
Да заместим тази функция в [26], като вземем предвид класическия импулс P=mv:
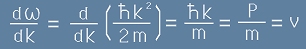 . [26.4]
. [26.4]
Виждаме, че груповата скорост представлява класическата скорост на материалната частица.
Орбитални нива
Вълновият вектор k има размерност 1/дължина и във фазата от [20], kx е безразмерно число.
По затворена крива, каквато е орбитата, произведението kx ще се изразява с линеен затворен интеграл,
но от Фиг.2 по-горе в тази страница се вижда, че такъв интеграл трябва да заема
стойности кратни на 2пи, тоест
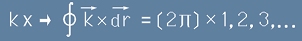 . [27]
. [27]
Ако умножим този интеграл по  , ще получим квантово
условие:
, ще получим квантово
условие:
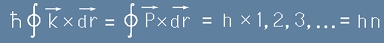 , [28]
, [28]
където h е константата на Планк, а n е цяло естествено, заемащо стойности 1,2,3...
Числото n е и първото от квантовите числа.
Дисперсия
По-горе (виж модулация и групова скорост) разбрахне, че при сбор от две дисперсни вълни,
едната се движи спрямо другата.
Същото се наблюдава и в пакета [17].
Ето една моя илюстрация на
движение на пакет без дисперсия
и
движение на пакет с малка дисперсия
.
Засега само да забележим, че съгласно казаното дотук, ако има дисперсия и сложно смесване,
както в [17], изобщо вълновият пакет не би трябвало да е стабилно образувание, а да се разсейва заради
разликите в груповите скорости на различните съставки. Ще оставя въпроса без отговор за момента.
Радостин Желязков 29.09.2011 ... редакция 24.10.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Материални вълни
Материални вълни


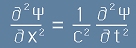 , [1]
, [1]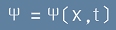 . [2]
. [2]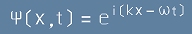 , [3]
, [3]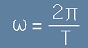 , [4]
с k е означено вълновото число:
, [4]
с k е означено вълновото число:
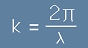 . [5]
. [5]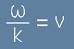 [5.1]
[5.1]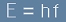 . [6]
. [6]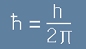 . [7]
. [7]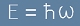 . [8]
. [8]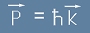 . [9]
. [9] Да разгледаме сбор две косинусови функции (защото такива съответствуват на реалната част от вълновото решение [3]).
Има едно известно тригонометричното тъждество за този случай:
Да разгледаме сбор две косинусови функции (защото такива съответствуват на реалната част от вълновото решение [3]).
Има едно известно тригонометричното тъждество за този случай: . [10]
. [10] , [11]
, [11]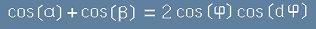 . [12]
. [12] . [13]
. [13] . [14]
. [14] ,
и нека
,
и нека
 . [15]
. [15] Скоростта на разпространение е всъщност условие за нулева фаза - първото от двете [15].
Скоростта на разпространение е всъщност условие за нулева фаза - първото от двете [15].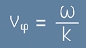 и се нарича още фазова скорост - същата е записана по-горе в [5.1].
и се нарича още фазова скорост - същата е записана по-горе в [5.1].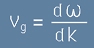 , [16]
, [16]
 . [17]
. [17] , [18]
, [18]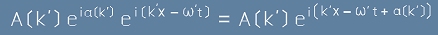 . [19]
. [19]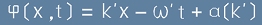 . [20]
. [20]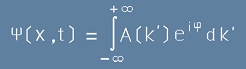 . [21]
. [21] е осцилираща експонента с фаза Фи,
е осцилираща експонента с фаза Фи,
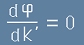 . [22]
. [22]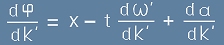 . [23]
. [23]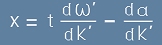 . [24]
. [24]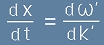 . [25]
. [25]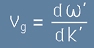 , [26]
, [26]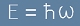 . [=8]
. [=8]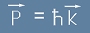 . [=9]
. [=9]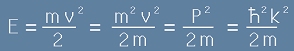 . [26.1]
. [26.1]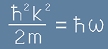 . [26.2]
. [26.2]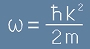 , [26.3]
, [26.3]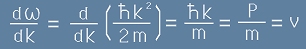 . [26.4]
. [26.4]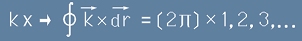 . [27]
. [27] , ще получим квантово
условие:
, ще получим квантово
условие: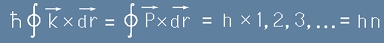 , [28]
, [28]