 Вълнови решения
Вълнови решения
Тази статия е за справка. Описано е едно решение на вълновото уравнение.
Тук са ползувани сведения от страници на Станчо Павлов:
Диференциални уравнения с разделящи се променливи,
Формули на Ойлер.
Има отношение към няколко други статии по физика, например:
Трептящ кръг,
Електромагнитни вълни,
Плоска вълна.
Материални вълни.
Уравнение на Лаплас
Нека f е функция на две променливи x и t.
Уравнението
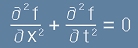 . [1]
. [1]
често е наричано Уравнението на Лаплас.
Ще потърсим каква е функцията f, за която [1] е вярно.
Експоненциалната функция f=ex има удобни, равни на себе си производни. Да предположим,
че търсената f е експонента:
 . [2]
. [2]
Първата и втората производна спрямо x са : първа 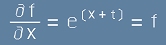 ,
втора:
,
втора: 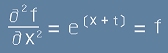 . [3]
. [3]
Първата и втората производна спрямо t са: първа 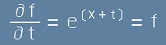 ,
втора:
,
втора: 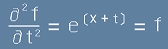 . [4]
. [4]
Сбора на горните две [3] и [4] в ляво ще даде [1], но от дясно остава изискването
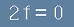 , [4.1]
, [4.1]
което при експоненциални функции няма как да е вярно.
Явно сбъркахме в предположението [2].
Да опитаме друго:
 . [5]
. [5]
Първата и втората производна спрямо x са : първа 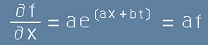 ,
втора:
,
втора:  . [6]
. [6]
Първата и втората производна спрямо t са : първа 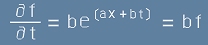 ,
втора:
,
втора:  . [7]
. [7]
Отново, сбора на [6] и [7] в ляво ще даде [1], а от дясно остава
 . [8]
. [8]
Ама че работа. Излиза, че сбора от квадратите на двата коефициента a и b трябва да е нулев.
Само имагинерните числа имат отрицателен квадрат. Едното от двете - a или b - трябва да е чисто имагинерно.
Стигаме до изискването
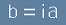 , където i е имагинерната единица.
, където i е имагинерната единица.
Следователно, ако (най-просто) a=1, то функцията
 [9]
[9]
е решение на [1]. Разбира се, x и t са симетрични аргументи и имагинерния множител може да е пред x,
тоест f=e(ix+t) е също решение.
Сега да опитаме да решим едно уравнение, близко до Лапласовото [1] :
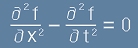 . [10]
. [10]
Ако повторим горните опити, тоест пак предполагаме [2],
пътя на равенствата [3] и [4] ще ни доведат до успех,
тъй като вместо фаталния сбор от [4.1] 2f = 0 , ще се появи разликата, която е тъждество f - f = 0.
Тоест [2] е пряко решение на [10]. Но да продължим по същия път. Чрез [6] и [7], можем да видим, че [5] е решение на [10] при a=b.
Но двата множителя a b може да са едновременно имагинерни и това ще запази решението, значи функцията
 [11]
[11]
е също решение на [10].
Сега да се обърнем към известното
Вълново уравнение
То много прилича на [10]:
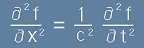 , [12]
, [12]
където c е някаква константа.
Да опитаме с хипотезата от [5]. Равенства [6] и [7] ще останат валидни.
Да умножим [7] с 1/c2:
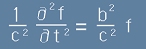 . [13]
. [13]
И да вземем разликата [6] минус [13]. Получаваме
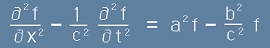 . [14]
. [14]
Виждаме, че условието, за да е вярно [12] е
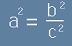 . [15]
. [15]
Това условие може да бъде спазено от чисто реални и от чисто имагинерни a b.
Изобщо двете версии - по-горната [5], както и следното, наричано някъде
Стандартно решение
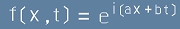 , [16]
, [16]
са решения на вълновото уравнение.
Обаче стандартното решение [16] има периодичен характер - погледнете статията на Станчо Павлов
Формули на Ойлер
и е избирано в общия случай, когато се очаква вълново явление.
Ойлеровият запис за експоненциалната функция от [16] е
 . [17]
. [17]
Имайки предвид Ойлеровото представяне на тригонометричните функции :
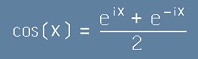 и още
и още
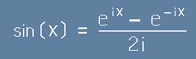 , [18]
, [18]
разбираме, че двете тригонометрични функции, в дясно на [17] :
 , [19]
, [19]
 , [20]
, [20]
представляват линейни комбинации
от стандартни решения и следователно са вълнови решения.
Радостин Желязков 01.10.2011 .. /последна корекция 10.10.2011/
________________________________________________________________________________________
коментари
учебни статии по физика
 Вълнови решения
Вълнови решения
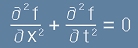 . [1]
. [1] . [2]
. [2]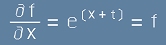 ,
втора:
,
втора: 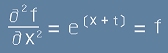 . [3]
. [3]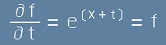 ,
втора:
,
втора: 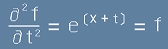 . [4]
. [4]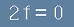 , [4.1]
, [4.1] . [5]
. [5]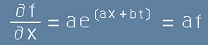 ,
втора:
,
втора:  . [6]
. [6]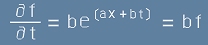 ,
втора:
,
втора:  . [7]
. [7] . [8]
. [8]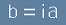 , където i е имагинерната единица.
, където i е имагинерната единица. [9]
[9]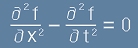 . [10]
. [10] [11]
[11]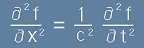 , [12]
, [12]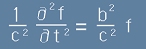 . [13]
. [13]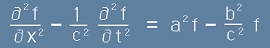 . [14]
. [14]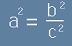 . [15]
. [15]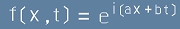 , [16]
, [16] . [17]
. [17]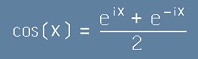 и още
и още
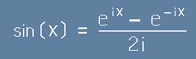 , [18]
, [18] , [19]
, [19] , [20]
, [20]