 Неопределеност на Хайзенберг
Неопределеност на Хайзенберг
Хайзенберг публикува тази си находка през 1927 г. - една година след уравнението на Шроьодингер.
Тук са ползувани предни статии:
Гаусово разпределение,
Материални вълни,
Преобразувание на Фурие.
Вълновият пакет
представлява линейна комбинация - интеграл,
за първи път споменат в предишната статия "Материални вълни" равенство [17].
Общо той изглежда като
 , [1]
, [1]
където f(k) е
Амплитудно разпределение
с пик k=k0 , в k-пространството (k е означение за вълнов вектор).
Ако мислено фиксираме времето в момент t=0, ще остане само зависимостта от k-вектора и горната линия би била
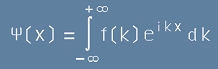 . [2]
. [2]
Да отбележим, че все още не знаем точния вид на разпределението f.
Нека допуснем за момент - като най-просто, че то е
нормално (Гаусово).
Около точката k=k0 и при стандартно отклонение = сигма,
Гаусовото разпределение би представлявало функция от вида :
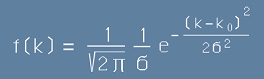 . [3]
. [3]
Това сигурно е грешно предположение, но ще го ползуваме за момента.
Да приемем временно означението
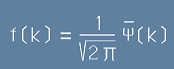 , [4]
, [4]
където  (Пси-черта) е неизвестния разпределител.
Да заместим това в [2]. Ще получим
(Пси-черта) е неизвестния разпределител.
Да заместим това в [2]. Ще получим
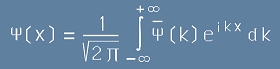 . [5]
. [5]
Сега е момента да си спомним за Преобразуванието на Фурие - равенство [24].
Последното равенство [5] е идентично с първото от Фурие-двойка.
Да запишем второто:
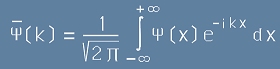 . [6]
. [6]
Ха! Излиза, че неизвестното разпределение е
Фурие-образ
на самата Пси-функция. Сега да уточним грубото предположение, което направихме по-горе в [3].
След казаното дотук виждаме, че правилната версия за разпределението трябва да е :
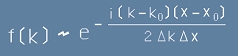 , [7]
, [7]
където вълничката (~) означава "е пропорционално на", a с делта k и x са означени стандартни отклонения,
тоест ширини на камбанките спрямо вектора k и координатата x.
Да съпоставим степенните показатели от [6] и [7].
Изразът -ikx от [6] няма записан знаменател, което е равносилно на знаменател 1.
Степенният показател от [7] има знаменател  .
Тези двата трябва да са равни и следователно
.
Тези двата трябва да са равни и следователно
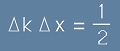 , [8]
, [8]
Имайки предвид израза за импулса
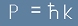 , [9]
, [9]
горният запис [8] води до едно
Известно отношение
между координатно и импулсно вероятностно отклонение
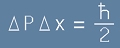 , [10]
, [10]
наричано Неопределеност на Хайзенберг.
Фурие-трансформациите имат в известен смисъл реципрочен характер.
Въпреки безкрайните граници при интегриране,
различните знаци в експоненциалните показатели, както и свързващата "трикова дефиниция" [21]
от статията за Фурие показват, че ненулевите области на двете функции и
двата аргумента са такива, че ако едната област се разширява, то другата се свива
и обратно.
Радостин Желязков 26.10.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Неопределеност на Хайзенберг
Неопределеност на Хайзенберг
 , [1]
, [1]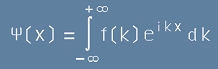 . [2]
. [2]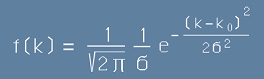 . [3]
. [3]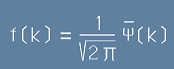 , [4]
, [4]  (Пси-черта) е неизвестния разпределител.
Да заместим това в [2]. Ще получим
(Пси-черта) е неизвестния разпределител.
Да заместим това в [2]. Ще получим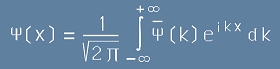 . [5]
. [5]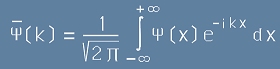 . [6]
. [6]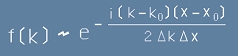 , [7]
, [7] .
Тези двата трябва да са равни и следователно
.
Тези двата трябва да са равни и следователно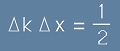 , [8]
, [8]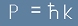 , [9]
, [9]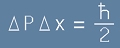 , [10]
, [10]