 Принцип на Ферма
Принцип на Ферма
Това е помощна статия. Други се обръщат към нея за справка.:
Има отношение към други статии:
Функция на Лагранж,
Принцип на Хамилтон,
Матриците на Хайзенберг.
Съгласно принципа на Ферма, вълната се разпространява така,
че времето за пристигане от началната до крайната точка е минимално.
Това време може да се представи като интеграл:
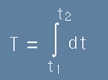 . [031]
. [031]
Вълновите процеси се разпространяват с ненулева скорост.
Можем да заменин интегралната променлива вместо време
с дължина мерена по пътя S на фронта на вълната:
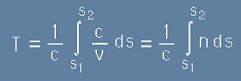 , [032]
, [032]
където c е константа, v е скоростта на вълната, а s1 и s2 са начална и крайна стойност на пътната променлива s, съответни на t1 и t2 от [0031].
n = c/v е коефициент на пречупване [може и да не е за на светлинна вълна].
Да предположим, че координатите x,y,z са функции на някакъв линеен параметър
тау ( ), който расте заедно с пътя на вълновия фронт. В такъв случай
), който расте заедно с пътя на вълновия фронт. В такъв случай
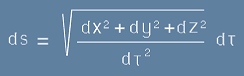 , [033] или по-удобно
, [033] или по-удобно
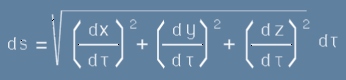 . [034]
. [034]
Да означим с L функцията:
 . [035]
. [035]
където n e скаларна функция на координатите, k е коефициент за размерност, с точка върху буква са отбелязани производните на координатите x y z по параметъра тау.
Тогава интегралът от по-горе [032] добива вид:
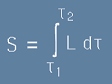 . [036]
. [036]
Тази постановка досущ прилича на описаната в началото от статията
"Принцип на Хамилтон".
L е функция от координати и скорости.
Коефициентът k от [035] е предназначен да осигури размерност на енергия за L.
Ако мислим за тау като за време, а за L като функция на Лагранж, то S отляво на [036] трябва да се асоциира с действие.
Радостин Желязков 08.10.2015
________________________________________________________________________________________
коментари
учебни статии по физика
 Принцип на Ферма
Принцип на Ферма
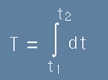 . [031]
. [031]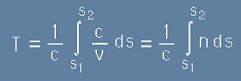 , [032]
, [032] ), който расте заедно с пътя на вълновия фронт. В такъв случай
), който расте заедно с пътя на вълновия фронт. В такъв случай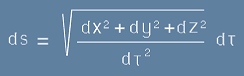 , [033] или по-удобно
, [033] или по-удобно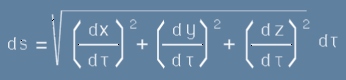 . [034]
. [034] . [035]
. [035]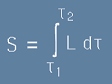 . [036]
. [036]