 Матриците на Хайзенберг
Матриците на Хайзенберг
Тук някои дефиниции и твърдения може да се повтарят с по-раншни.
Желателно е запознаване с преднишни статии:
Принцип на Хамилтон,
Вълнови решения,
Материални вълни,
Уравнение на Шрьодингер,
Оператори,
Уводът на Ландау,
Принцип на Ферма.
Средни стойности
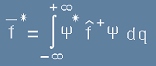
В класическата механика дефиницията за средни стойности се базира на интеграли
от непрекъснати функции. При дискретно множество, каквото са квантово-механичните собствени
стойности е нужна друг тип дефиниция. Такава е (18 от предната статия). Да я запишем отново:
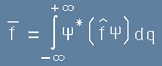 . [1]
. [1]
означения:
шапка над буква е оператор; черта над буква е средна стойност.
звездичка горе в дясно е комплексно спрегната на означената величина.
комплексно спрегнат оператор е този, чието прилагане върху комплексно-спрегнатата функция
води до комплексно-спрегнат резултат спрямо резултата от f(пси):
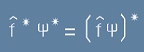 . [1y]
. [1y]
Когато оператоът f има класически аналог, средната стойност трябва да е реална, затова изразът в дясно на [1] трябва да е равен на своя комплексно-спрегнат.
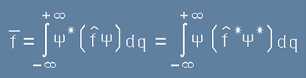 . [2]
. [2]
Оператори, спазващи такова условие се класират като ермитови, или като самоспрегнати оператори.
Транспониран оператор
Транспонирането се означава с вълничка отгоре.
По дефиниция транспониран оператор е този, който за две функции ФИ и Пси работи
по следния начин:
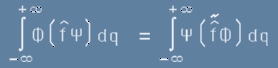 . [012]
. [012]
Ако вместо Фи поставим комплексно-спрегнатата на Пси функция, от [2] е видно, че за ермитовите оператори важи равенството:
 . [013]
. [013]
Тоест за Ермитови оператори комплексно-спрегнатият е равен на транспонирания.
Спрегнат и комплексно спрегнат
Да допуснем формално, че има комплексна физична величина f (тоест нейните собствени стойности са комплексни). Нека тя съответства на оператор f.
За нейната комплексно-спрегната стойност f* трябва да се прилага друг оператор, който се
нарича "спрегнат" на f.
Той се означава с плюс горе вдясно  и е различен от известния ни досега комплексно-спрегнат оператор от по-горе [1y].
По дефиниция:
и е различен от известния ни досега комплексно-спрегнат оператор от по-горе [1y].
По дефиниция:
 . [014]
. [014]
От друга страна, прякото пресмятане на [1] (виж [012]) дава:
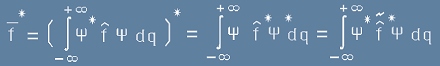 , [015]
, [015]
откъдето (съпостави [015] и [014) се вижда, че
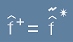 [016]
[016]
- тоест между "комплексно спрегнат оператор" и "спрегнат оператор" има разлика.
Граничен преход
В класическата физика електронът е частица, движеща се по траектория. В квантовата механика
той се описва като вълна. Функцията -
решение на вълновото уравнение
- представлява
най-общо
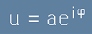 . [3]
. [3]
където буквата а означава бавно меняща се амплитуда, а фазовият ъгъл фи расте с времето и заема големи стойности.
Траекторията на частицата се определя по
принципа за най-малкото действие.
За справка виж статията Принцип на Ферма.
Принципът на Ферма е еквивалент на принципа на Хамилтон, за вълновото разпространение. Според него вълната се движи по най-краткия фазов път (минимално фи от формула [3]).
Ако трябва да приложим това за вълновата функция, степеннният показател от [3] трябва да е пропорционален на действие. Действието се означава с буква S.
За да бъде степенния показател безразмерно число, коефициентът на пропорция трябва да с размерност 1/S. За единично действие се приема константата на Планк
(Виж равенство 7 от статията
Материални вълни
Материални вълни
)
. След тези съображения
видът на вълновата функция е:
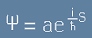 . [4]
. [4]
Енергия
Вълновата функция напълно определя квантово-механичната система. Това значи, че и бъдещото поведение е определено от същата вълнова функция. Щом е така, то производната на Пси по времето
трябва да се получава с линеен оператор от самото Пси, с някакъв коефициент:
 . [5]
. [5]
В равенството [5] оградената с кръгче буква k е неизвестен коефициент, а H
трябва да е някакъв линеен оператор.
Да вземем производната на [4] пропускайки амплитудния множител a, който се мени бавно с времето:
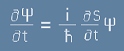 . [6]
. [6]
От [6] виждаме, че в граничния случай прилагането на предполагаемият линеен оператор H се свежда до умножение по производната на действието S по времето.
Действието има размерност енергия по време, така че производната му по време е енергия.
Операторът H от [5] съвпада по класически смисъл с функцията на Хамилтон.
Той работи, както се вижда от [6] по следния начин:
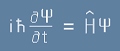 . [7]
. [7]
Производна на оператор по времето
В класическата механика производните се дефинират върху гладки непрекъснати функции.
В дискретния случай това не е възможно. Но да вземем производната на кой да е оператор от [1] по времето
(пропускаме скобите, когато поредността е достатъчна):
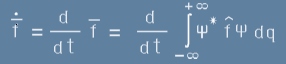 . [8]
. [8]
По-точно
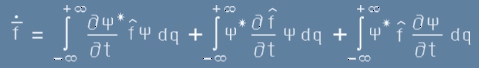 . [9]
. [9]
Да забележим, че съгласно [7] двете производни на пси и пси* по времето са:
 . [10]
. [10]
Заместваме това в [9]:
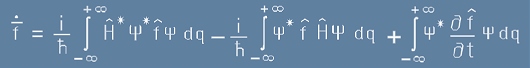 . [11]
. [11]
Да преподредим подинтегралната функция от първото събираемо, замествайки
комплексно-спрегнатия оператор H с неговия транспониран, защото H е ермитов оператор - виж по-горе [013]:
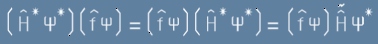 . [12]
. [12]
И сега да забележим как се записва първия интеграл от [11] (без множителя отпред), според правилото за транспониране от по-горе в [012]:
 . [13]
. [13]
Заместваме [13] в [11] и се приближаваме към по-прегледена вид на производната от [8]:
 . [14]
. [14]
От тук става ясно, че операторът съответен на производната по времето има вид:
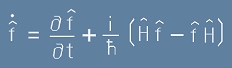 . [15]
. [15]
Ако операторът не зависи явно от времето, частната му производна - първото събираемо в [15] - ще е нула и ще остане само изразът в скобите - комутаторът [H,f]. От тук се вижда, че ако този комутатор също е нулев, то самата величина f ще е запазваща се.
Стационарни състояния
Стационарни са тези състояния, в които енергията има определена стойност En.
Те се описват от Пси-функции  ,
които са собствени функции на оператора H. Тези пси-функции са решения на уравнението:
,
които са собствени функции на оператора H. Тези пси-функции са решения на уравнението:
 . [16]
. [16]
Знаейки от по-горе [7] как работи H-оператора:
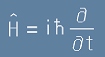 , [17]
, [17]
заместваме [17] в [16] и съставяме следното уравнение:
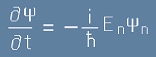 . [18]
. [18]
То се интегрира пряко и получаваме вид на Пси-функциите:
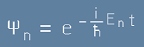 [19]
[19]
Обаче тези разсъжения важат само за зависимост от времето. Пси-функциите [19] не са
локализирани никъде в пространството. Поместването става с амплитуден множител (погледнете по-горе [4]; Освен това си спомнете за свободата от статията
Оператори, [6] и [7])
). Могат да се представят вместо [19] направо като:
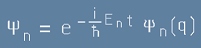 , [20]
, [20]
където с малко пси 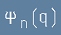 са означени функции зависещи само от координатите q.
са означени функции зависещи само от координатите q.
Пси фунцкцията е сбор на индексирани с "n" енергетични състояния от [20]:
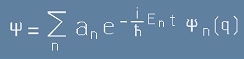 , [22]
, [22]
където модулът на комплексните "a" - коефициенти е вероятността за n-тото състояние (виж
равенства [1][2][3] от предната статия ).
За едно стационарно състояние, вероятностното разпределението на координатите е:
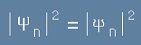 , [23]
, [23]
то не зависи от времето.
Матрици
Да предположим, че енергията е дискретно разпределена, тоест
 . [24]
. [24]
Да заместим [24] в [1]:
 [25]
[25]
и да уговорим кратко означение от вида:
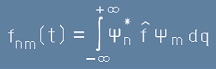 . [26]
. [26]
Тук интегрирането става по координати, но остава зависимост от времето чрез Пси функциите вътре в интеграла, затова е указано fnm(t).
И така стигаме до равенството:
 , [27]
, [27]
в което n m са индекси на две различни стационарни състояния.
Означеното с малка буква fnm(t) се нарича матрица на величината f; Всеки fnm-елемент съответства на преход от състояние m в състояние n.
Да заместим известния от по-горе [20] вид на Пси-функцията в равенство [26]:
 . [28]
. [28]
В двете експоненти не виждаме зависимост от координатите, следователно те подлежат на разместване:
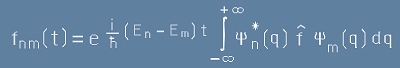 . [29]
. [29]
Участъкът от горната формула
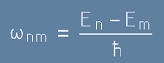 [30]
[30]
е честота на енергийния преход - видим в обикновения свят като спектрална линия,
а елементите на матрицата на прехода не зависят от времето и представляват интеграли от вида:
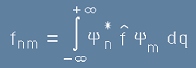 , [31]
, [31]
където малките пси-букви означават функции само от координатите q.
С матрици от този вид може да се оперира, подобно на матричната алебра.
Tе са били въведени за първи път от Хайзенберг 1925, още преди вълновото уравнение.
Понякога вместо [31] се ползва означението:
 , [32]
, [32]
Въведено малко по-късно от Дирак. Това се нарича и бра-кет записване.
Радостин Желязков 03.10.2015 последна редакция 08.10.2015
________________________________________________________________________________________
коментари
учебни статии по физика
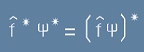 . [1y]
. [1y]
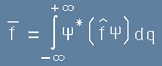 . [1]
. [1]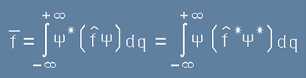 . [2]
. [2]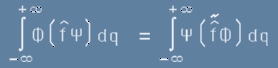 . [012]
. [012] . [013]
. [013] и е различен от известния ни досега комплексно-спрегнат оператор от по-горе [1y].
По дефиниция:
и е различен от известния ни досега комплексно-спрегнат оператор от по-горе [1y].
По дефиниция: . [014]
. [014]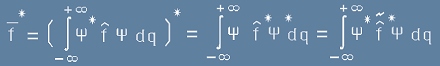 , [015]
, [015]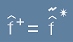 [016]
[016]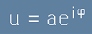 . [3]
. [3]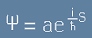 . [4]
. [4] . [5]
. [5]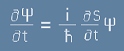 . [6]
. [6]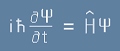 . [7]
. [7]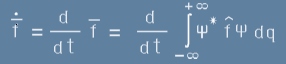 . [8]
. [8]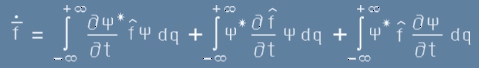 . [9]
. [9] . [10]
. [10]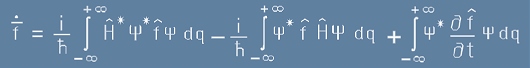 . [11]
. [11]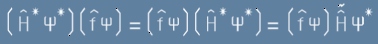 . [12]
. [12] . [13]
. [13] . [14]
. [14]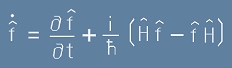 . [15]
. [15] ,
които са собствени функции на оператора H. Тези пси-функции са решения на уравнението:
,
които са собствени функции на оператора H. Тези пси-функции са решения на уравнението: . [16]
. [16]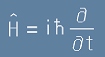 , [17]
, [17]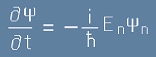 . [18]
. [18]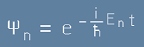 [19]
[19]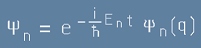 , [20]
, [20]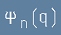 са означени функции зависещи само от координатите q.
са означени функции зависещи само от координатите q.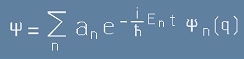 , [22]
, [22]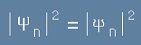 , [23]
, [23] . [24]
. [24] [25]
[25]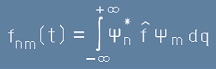 . [26]
. [26] , [27]
, [27] . [28]
. [28]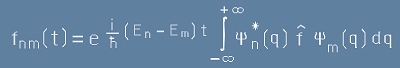 . [29]
. [29]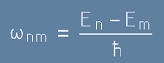 [30]
[30] , [31]
, [31] , [32]
, [32]